Dérivation (1)
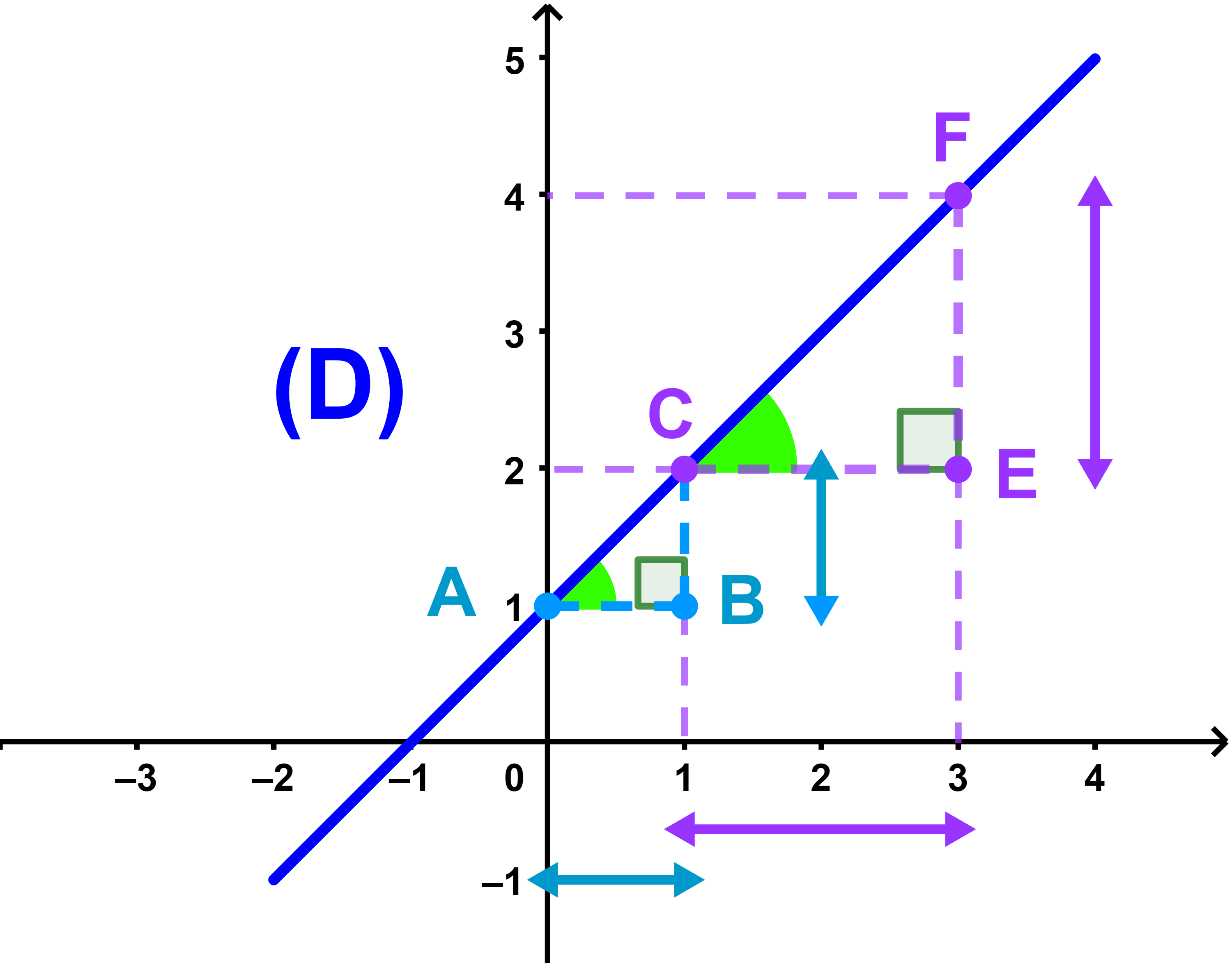
Rappel Soient A et C deux points diffréents d'une droite (D) le nombre
| m = | yC - yA |
| xC - xA |
est appelé coefficient directeur de (D).
L'équation réduite de (D) s'écrit sous la forme
y=mx+p tel que p est l'ordonnée à l'origine.
Nombre dérivé et équation de la tangente
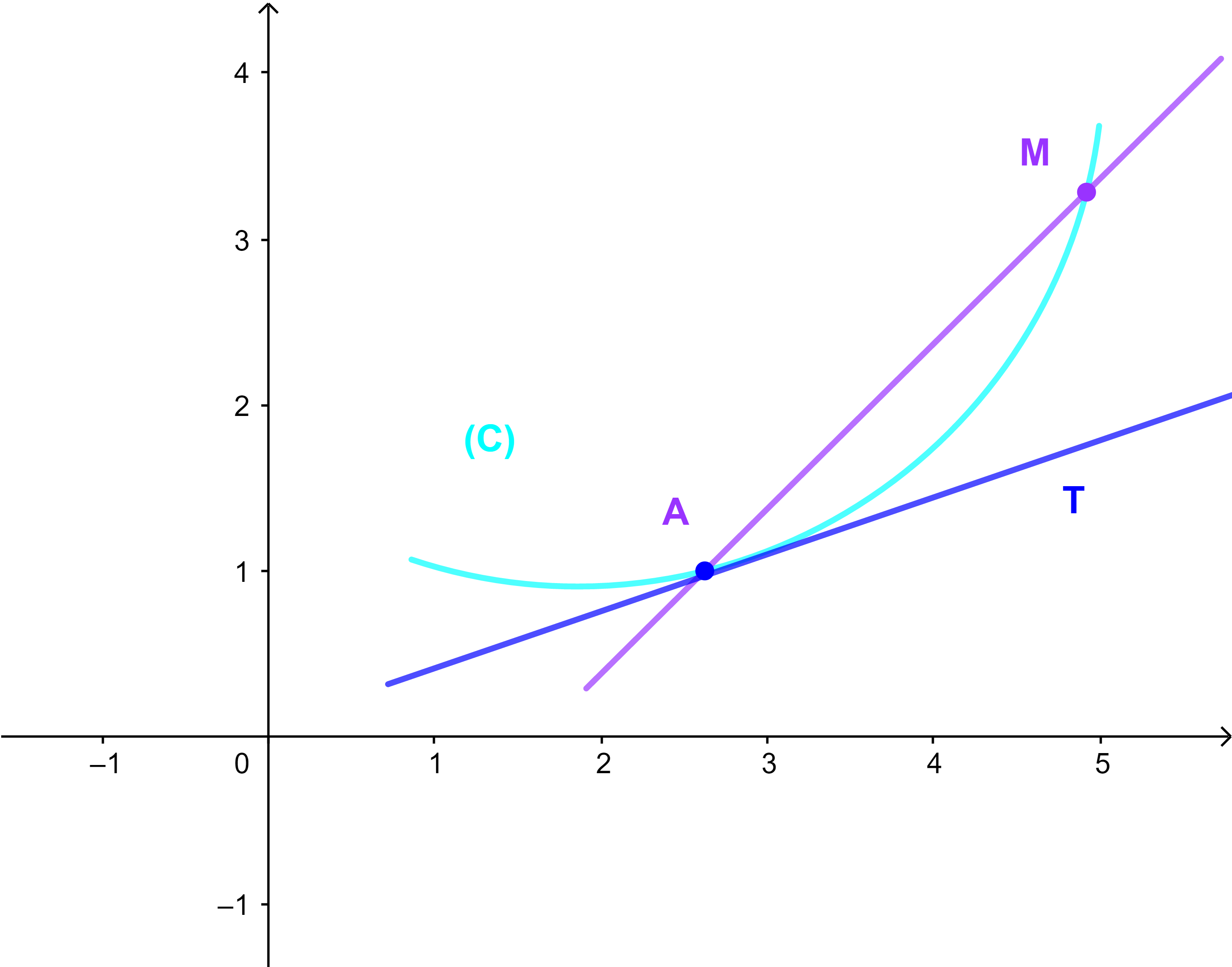
Soient f une fonction définie sur un intérvalle I et a∈I et (C) sa courbe représentative dans un repère orthonormé (O;i→;j→)
f est dérivable au point a signifie qu'il existe
un réel L tel que
lim x→a |
f(x) - f(a) | = L |
| x-a |
L est le nombre dérivé de f en a
noté f'(a)
La courbe (C) admet une tangente au point A(a;f(a)) de coefficient directeur f'(a) et son équation s'écrit sous la forme
y=f'(a)(x-a)+f(a)
Opérations sur les limites
1) Soient f et g deux fonctions dérivables sur I et n∈IN*
les fonctions f + g ; k.f ; f×g et f n sont également dérivables sur I et pour tout x∈I
| (f + g)'(x) | = | f'(x) + g'(x) |
| (k.f)'(x) | = | k.f '(x) |
| (f g)'(x) | = | f '(x)g(x) + f(x)g '(x) |
| (fn)'(x) | = | nfn-1(x)f '(x) |
(∀x∈IR): (xn)' = nxn-1
Notons que toute fonction polynôme est dérivable sur IR
Soientt f et g deux fonctions dérivables sur un intervalle I
Si g ne s'annule pas sur I alors l'inverse de g et le quotien de f sur g sont dérivables sur I. Soit x∈I
| ( | 1 | )'(x) = | - g '(x) |
| g | (g(x))² |
| (∀x∈I)/ ( | f | )'(x) = | f'(x)g(x) - f(x)g'(x) |
| g | (g(x))² |
Notons que toute fonction rationnelle est dérivable sur son ensemble de définition D
Monotonie
1) Soit f une fonction dérivable sur I
f est croissante sur I ⇔ (∀x∈I) f'(x)≥0
f est décroissante sur I ⇔ (∀x∈I) f'(x)≤0
f est constante sur I ⇔ (∀x∈I) f'(x)=0.
2) Soit f une fonction dérivable sur I
f est strictement croissante sur I
⇔ (∀x∈I) f'(x)>0
f est strictement croissante sur I
⇔ (∀x∈I) f'(x)<0
Extremum
1) Soit f une fonction définie sur I et a∈I
On dit que f(a) est un extremum de f sur I s'il est valeur minimale ou valeur maximale.
2) Soit f une fonction dérivable sur I et a∈I
Si f admet un extremum au point a
alors f'(a)=0
3) Soit f une fonction dérivable sur I et a∈I
Si f' s'annule en a et change de signe au voisinage de a
alors f(a) est un extremum.