1- المجموعة المنتهية

1.1 تعريف وترميز

1.1.1 امثلة

1) نعتبر المجموعة E={-2;3;7;10}.
E مجموعة مكونة من خمسة عناصر
نقول اذن E مجموعة منتهية.
2) نعتبر المجموعة F={x∈IR/ x≥0}
F مجموعة مكونة مما لانهاية من العناصر نقول اذن F مجموعة غير منتهية.

1.1.2 تعريف

نقول ان E مجموعة منتهية اذا كان عدد عناصرها عدد حقيقي ونرمز له ب card(E) ويسمى رئيسي E.

أمثلة
1) E={-3;-1;0;7;8;12;17;23} مجموعة مكونة من 8 عناصر اذن E مجموعة منتهية و cardE=8.
2) F={0;1;2;3;4} مجموعة مكونة من 5 عناصر اذن F مجموعة منتهية و cardF=5.
3) ∅={} مجموعة فارغة أي لا تحتوي على أي عنصر card(∅)=0.

1.2 تقاطع مجموعتين منتهيتين

1.2.1 مثال

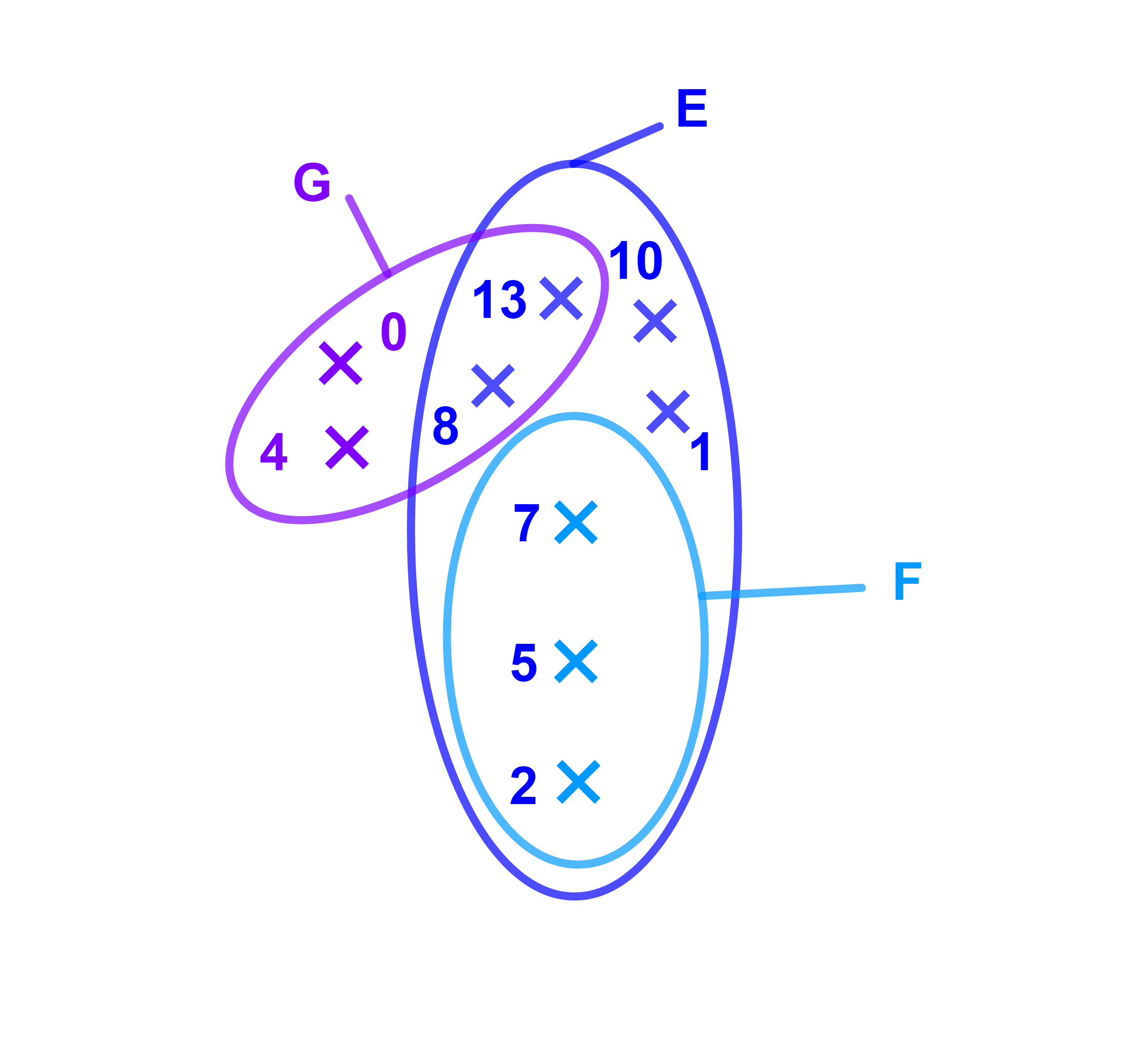
لتكن E={1;2;3;4;5;7}
و F={-3;-2;0;1;5;7;10;13}
و G={-2;10;15;20} ثلاث مجموعات.
1) العناصر المشتركة بين المجموعتين E و F هي 1 ; 5 ; 7 نقول ان المجموعة {1;5;7} هي تقاطع المجموعتين E و F
ونكتب E ∩ F={1;5 ;7}.
2) لا يوجد اي عنصر مشترك بين المجموعتين E و G
نقول ان E و G منفصلتان ونكتب E∩G=∅.

1.2.2 تعريف

لتكن E و F مجموعتين منتهيتين.
تقاطع المجموعتين E و F ونكتب E∩F مجموعة العناصر المشتركة بينهما
وبعبارة اخرى
E∩F={x / (x∈E و x∈F)}.

1.3 اتحاد مجموعتين منتهيتين

1.3.1 مثال

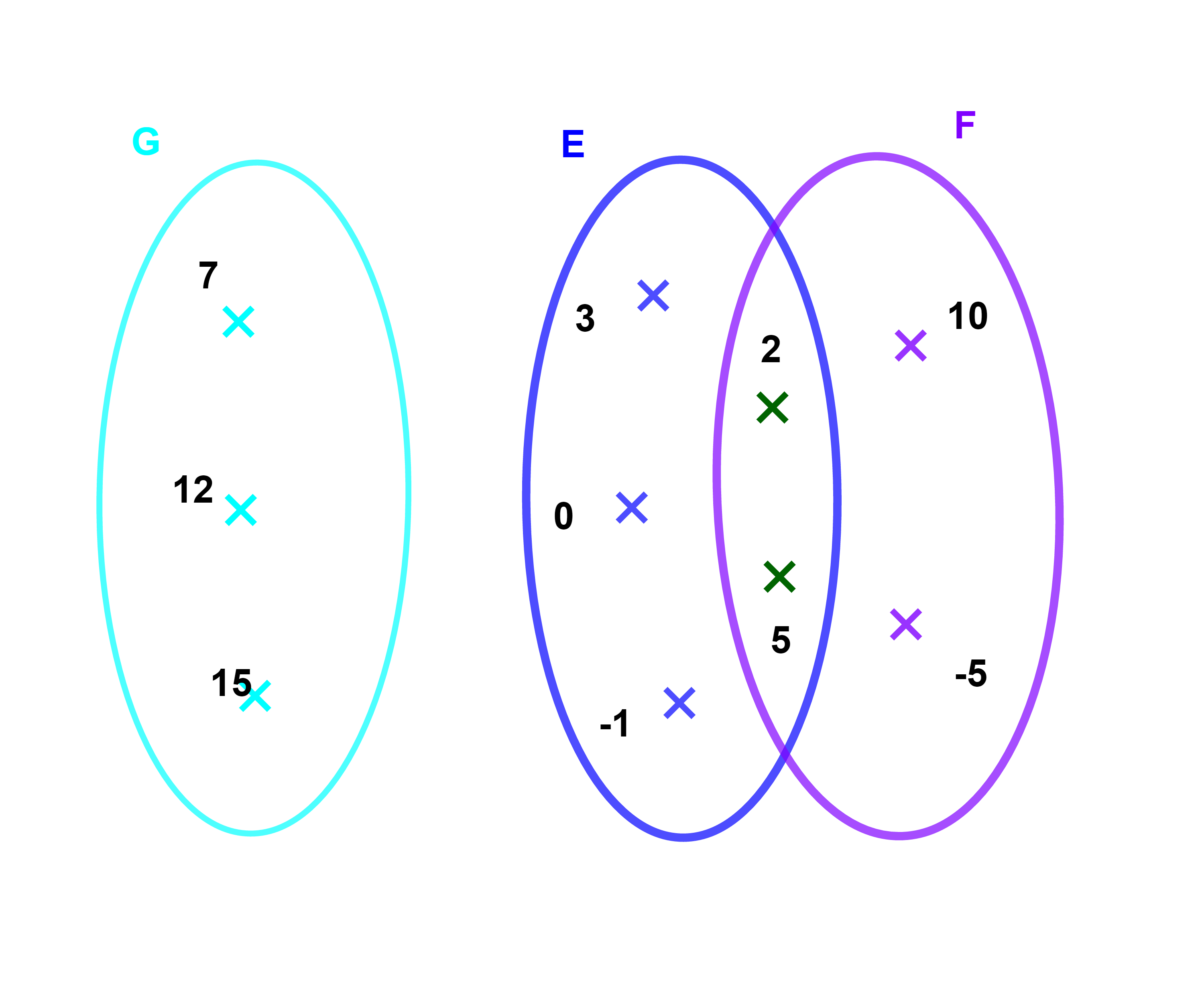
لتكن E={-1;0;2;3;5} و F={-5;2;5;10} و G={7;12;5} ثلاث مجموعات منتهية.

المجموعة المكونة من عناصر E و F
هي {-5;-1;0;2;3;5;10} وتسمى اتحاد E و F ونكتب E∪F.

1.3.2 تعريف

اتحاد مجموعتين E و F ونكتب E∪F هو المجموعة المكونة من عناصر E و F.

وبعبارة اخرى
E∪F={x / (x∈E او x∈F)}.

ملاحظة E∪F=F∪E.

1.3.3 خاصيات

لتكن E و F مجموعتين منتهيتين.
1) اذا كان E∩F=∅ فان
card(E∪F)=cardE+cardF.
2) اذا كان ∅≠E∩F فان
card(E∪F)=cardE+cardF-card(E∩F).

تمرين 1 tp

حدد مبيانيا E∪F و E∪G و E∩G و F∩G.