1- Ensemble fini

1.1 Définition et notaion

1.1.1 Exemples

1) On considère l'ensemble E={-2 3;7;10}.
L'enemble E est constitué de quatre éléments
on dit donc que E est un ensemble fini.
2) Soit F={x∈R/ x>0}.
L'ensemble F est constitué d'une infinité d'éléments, on dit donc que F est un ensemble infini.

1.1.2 Définitions

1) On dit qu'un ensemble est fini s'il est constitué d'un nombre fini d'éléments.
2) Le nombre d'éléments d'un ensemble fini E est appelé cardinal de E, noté cardE.

Exemples
1) E={-3;-1;0;7;8;12;17;23} est un ensemble fini et cardE=8.
2) ∅={} est un ensemble vide et card∅=0.

1.2 Intersection de deux ensembles finis

1.2.1 Exemple

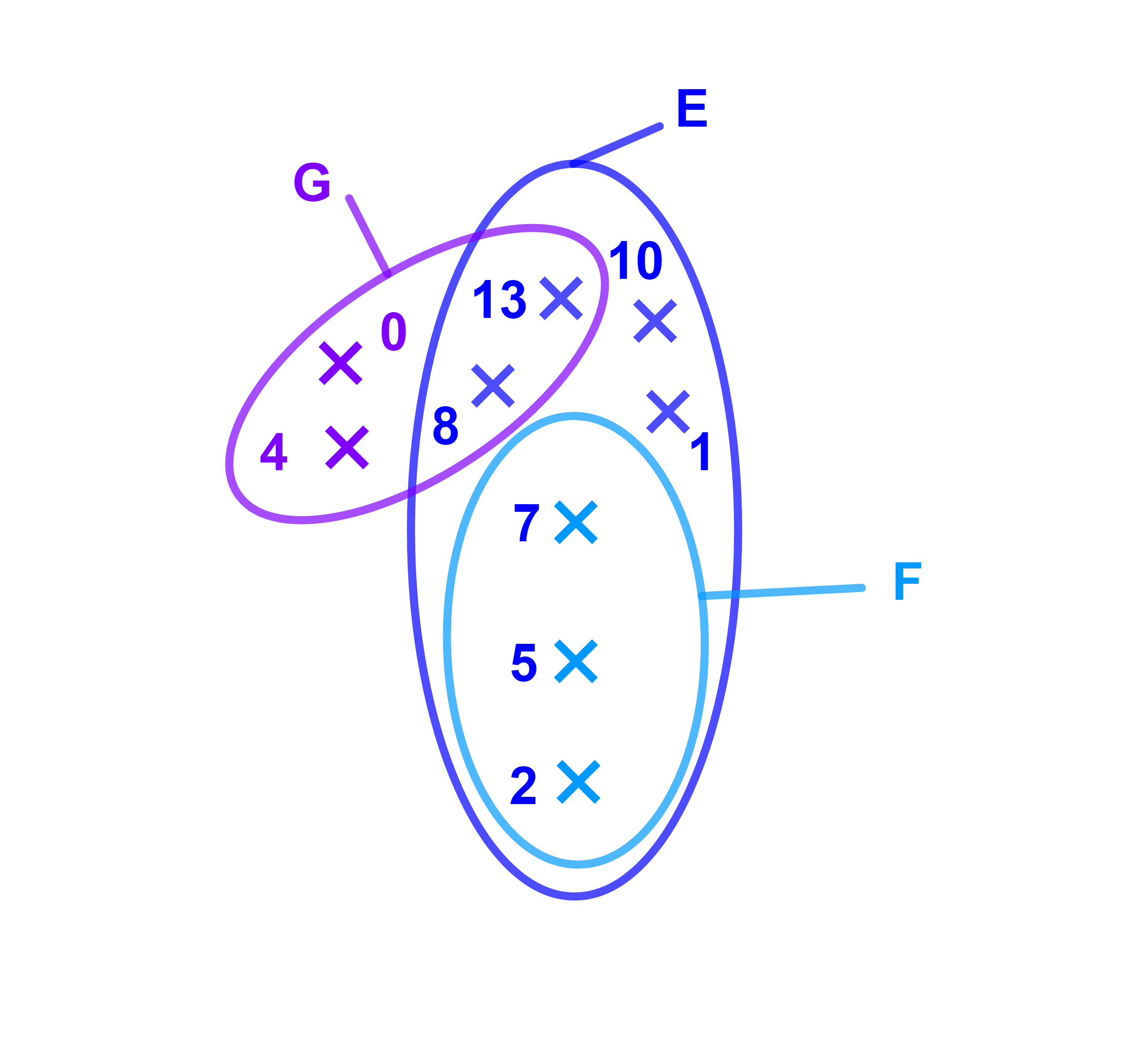
Soient E={1;2;3;4;5;7}
F={-3;-2;0;1;5;7;10;13}
et G={-2;10;15;20} trois ensembles.
1) Les éléments communs entre E et F sont 1 ; 5 et 7, on dit que l'ensemble {1;5;7} est l'intérsection de E et F
noté E∩F={1;5;7}.

2) Il n y'a aucun élément commun entre E et G, on dit que E et G sont disjoints
et on écrit E∩G=∅.

1.2.2 Définition

Soient E et F deux ensembles finis.
L'intersection de E et F, noté E∩F est l'ensemble des éléments communs entre eux.
En d'autre terme
E∩F={x/(x∈E) et (x∈F)}.

1.3 Union de deux ensembles finis

1.3.1 Exemple

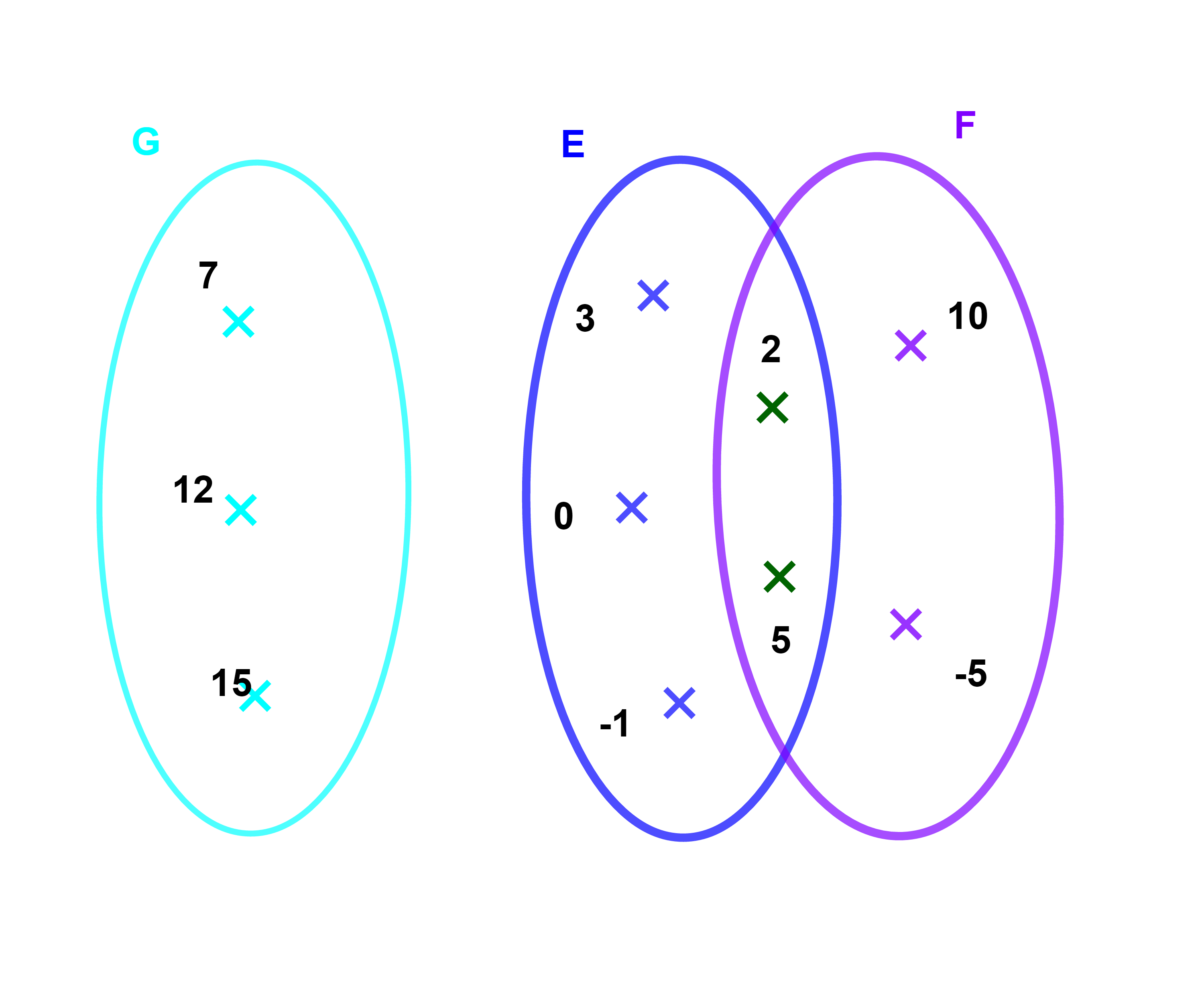
Soient E={-1;0;2;3;5}
F={-5;2;5;10} et G={7;12;15} trois ensembles finis.
L'ensemble constitué par des éléments de E et F, {-5;-1;0;2;3;5;10} est appelé union de E et F et est noté E∪F.

1.3.2 Définition

Union de deux ensembles E et F, noté E∪F est l'ensemble des éléments de E et F.

En d'autre terme
E∪F={x/(x∈E) ou (x∈F)}.

Remarque E∪F=F∪E

1.3.3 Propriétés

Soient E et F deux ensembles finis
1) Si E∩F=∅ alors
card(E∪F)=cardE+cardF.
2) Si (E∩F)≠∅ alors
card(E∪F)=cardE+cardF-card(E∩F).

Exercice 1 tp

Déterminer E∪F; E∪G ; E∩G et F∩G.