2- Principe du dénombrement

2.1 Principe du produit

2.1.1 Définition

Dans une expérience à k étapes, si la 1ière étape s'éffectue de n₁ manières différentes, la 2ième étape s'éffectue de n₂ manières différentes et ainsi de suite jusqu'à la kième étape qui s'éffectue de n_k manières différentes alors la suite de ces étapes s'éffectue de n₁×n₂×...×n_k manières différentes.

C'est ce qu'on appelle le principe fondamental du dénombrement.

2.1.2 Exemple

Si une personne a 3 chemises; 4 pantalons et 2 paires de chaussures alors elle a 3 possibilités pour porter une chemise; 4 possibilités pour porter un pantalon et 2 possibilités pour porter des chaussures.
D'après le Principe fondamental du dénombrement, le nombre de tenues différentes est 3×4×2=24.

2.2 Arbre de choix

2.1.1 Exemple 1

1) Lorsqu'une pièce de monnaie est lancée en l'air, le face F ou le pile P apparait
le nombre de résultats possibles est deux, P ou F.
L'ensemble W={F;P} est appelé ensemble d'éventualités et cardW=2.

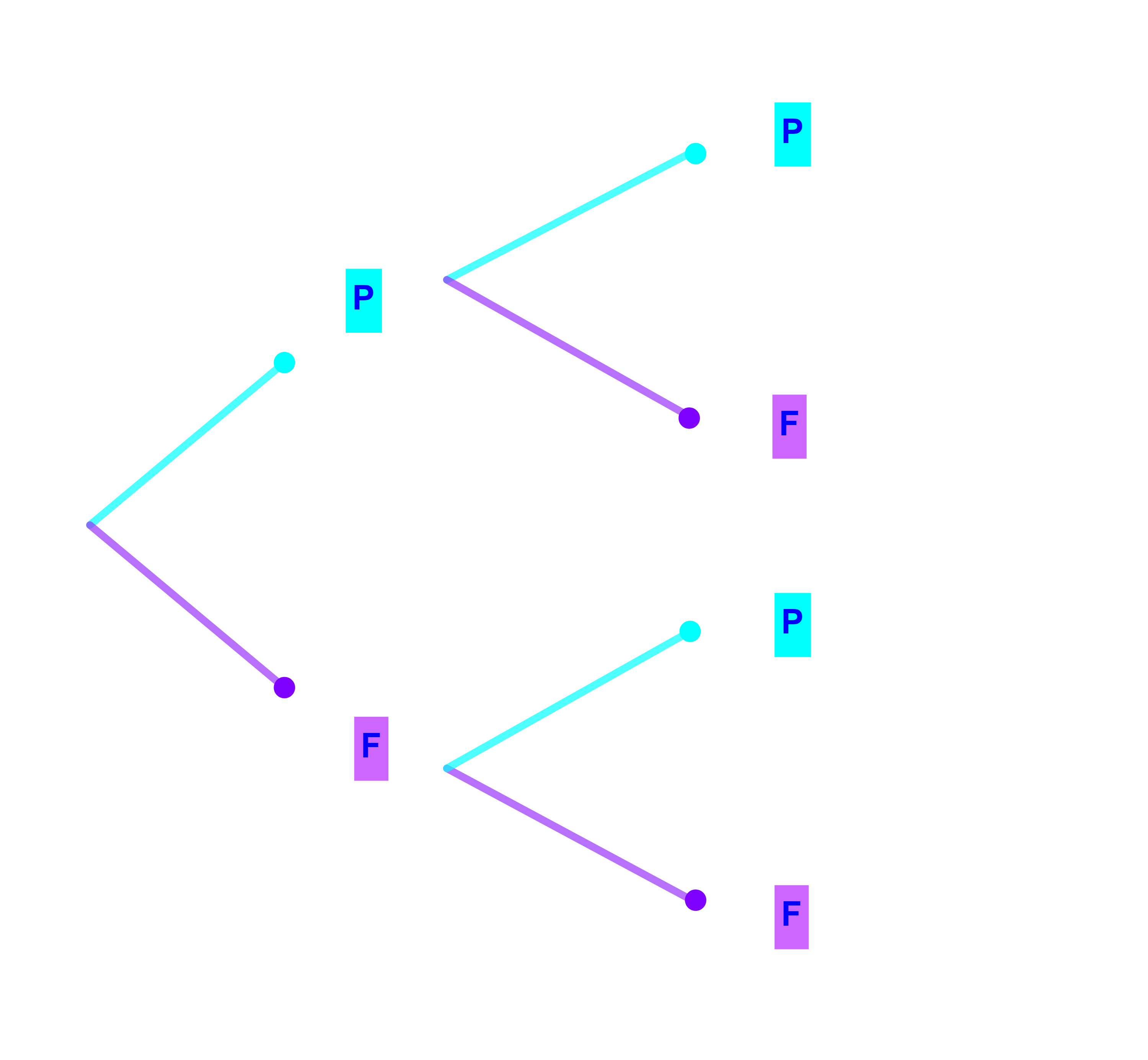
2) Lorsqu'une pièce de monnaie est lancée deux fois consécutives, le nombre de résultats possibles est 2×2=4.
W={FF;FP;PF;PP} et cardW=4.

2.1.2 Exemple 2

Une urne contient 5 jetons numérotés de 1 à 5.
1 2 3 4 5
Lorsqu'un jeton est tiré, l'un des nombres 1 ou 2 ou 3 ou 4 ou 5 apparait
donc il existe 5 possibilités.

Les résultats obtenus constituent un ensemble appelé ensemble d'éventualités
W={1;2;3;4;5} et card(W)=5.