للتذكير
الفروع اللانهائية 1) لتكن f دالة عددية ذات المتغير x و (C) المنحنى الممثل لها في معلم متعامد ممنظم
(O ; i^→ ; j^→)
اذا كان احدى احداتيات نقطة M(x ; y)∈(C) يؤول الى ما لانهاية فان للمنحنى (C) فرعا لانهائيا
يعني عندما ( x→±∞ او f(x)→±∞)

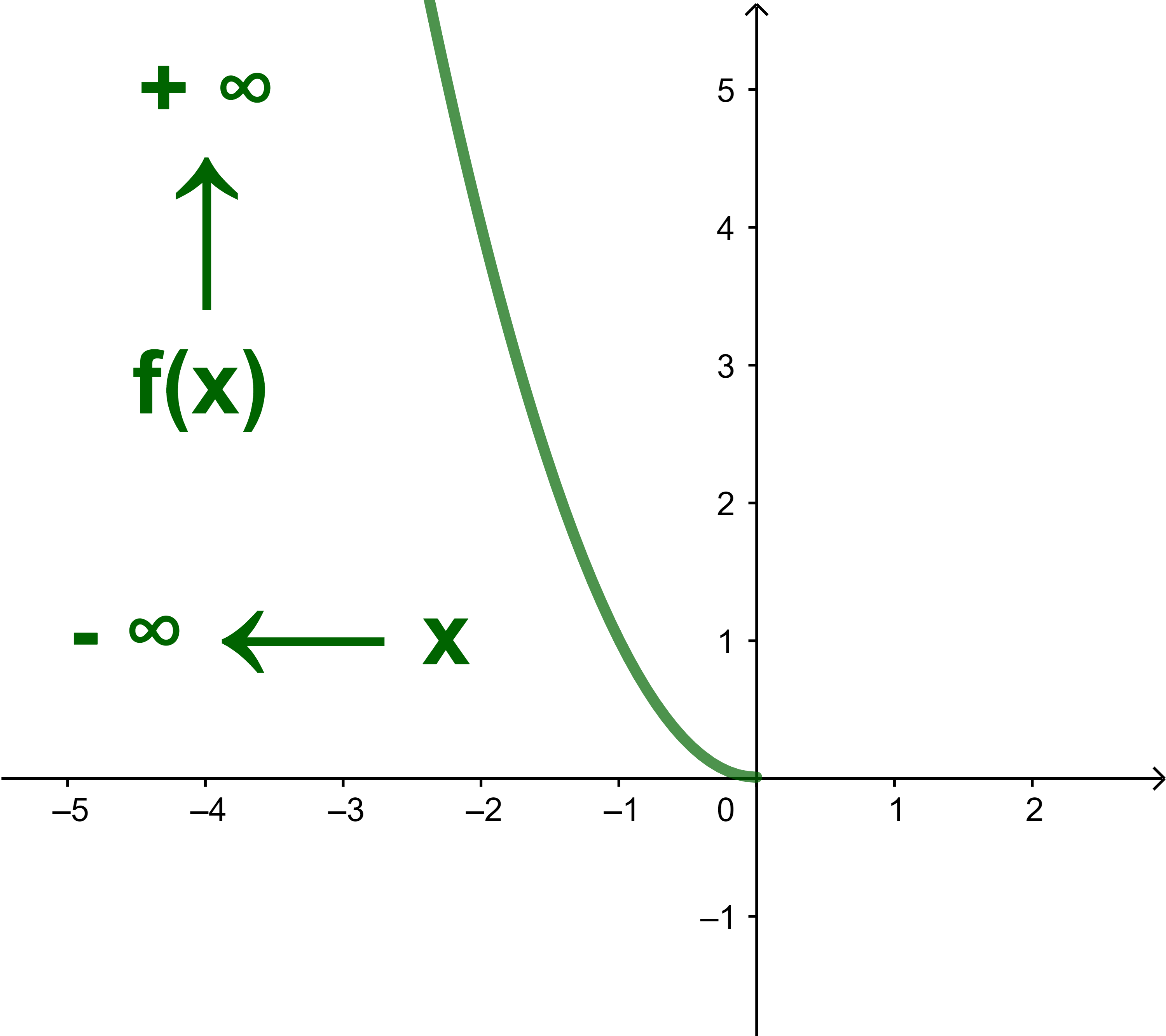
الحالة التي تؤول الاحداثيتان معا الى ما لانهاية
( x→-∞ و f(x)→+∞)

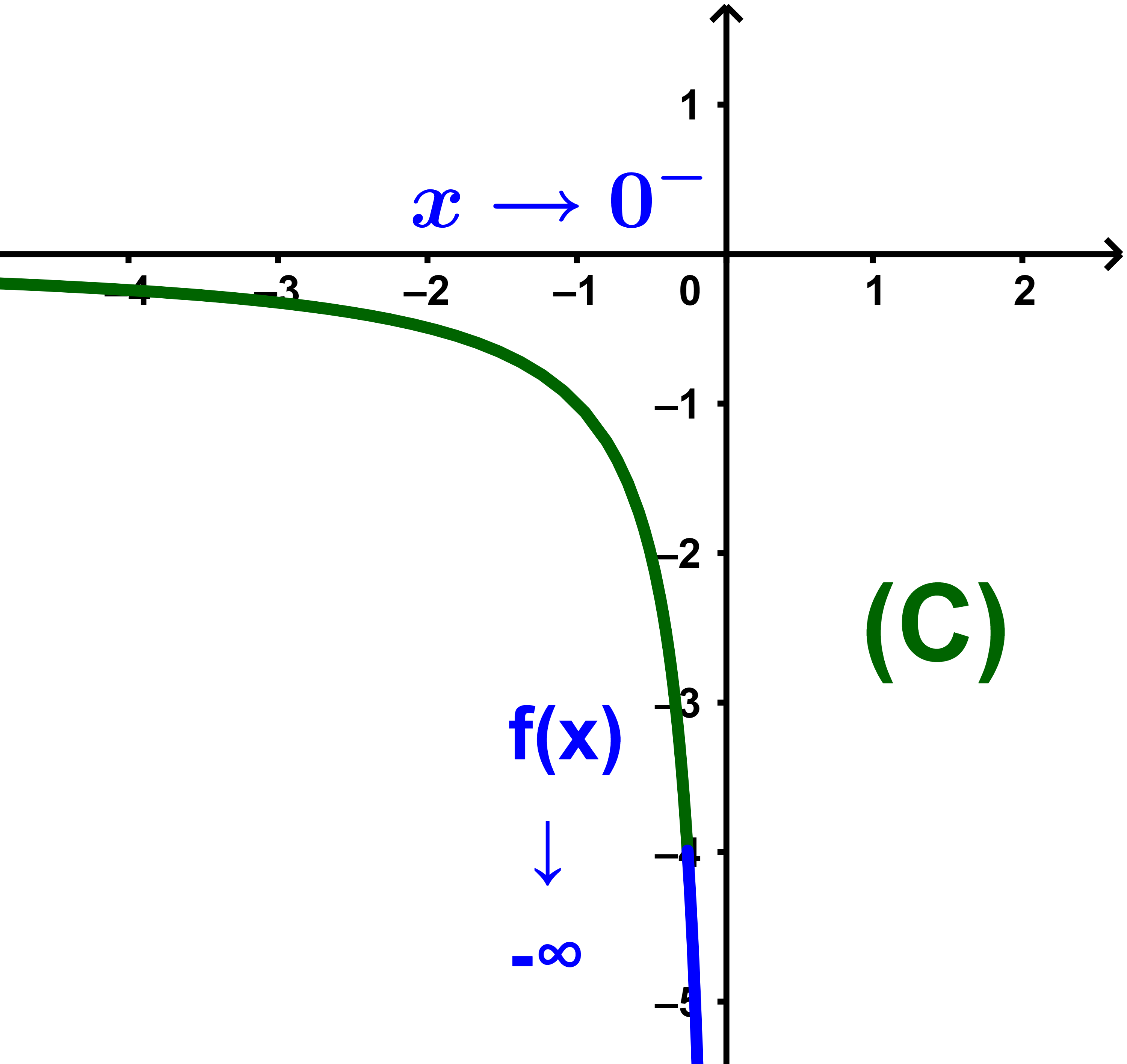
الحالة التي تؤول y=f(x) الى ما لانهاية
(f(x)→ - ∞)

2) لتكن f دالة عددية ذات المتغير x و (C) المنحنى الممثل لها في معلم متعامد ممنظم
(O ; i^→ ; j^→)
اذا كان احد الشروط التالية محققا

lim a-	f(x) = +∞		lim a-	f(x) = -∞
lim a+	f(x) = +∞		lim a+	f(x) = -∞

فان المستقيم ذو المعادلة x = a
مقارب للمنحنى (C)

3) لتكن f دالة عددية ذات المتغير x و (C) المنحنى الممثل لها في معلم متعامد ممنظم
(O ; i^→ ; j^→)
(i) اذا كان

lim -∞

f(x) = b

; b∈IR

فان المستقيم ذو المعادلة y = b مقارب (C) بجوار - ∞
(ii) اذا كان

lim + ∞

f(x) = b

; b∈IR

فان المستقيم ذو المعادلة y=b مقارب (C) بجوار +∞.