تمرين 1 tp

لتكن f دالة عددية معرفة كما يلي

f(x) =	-2x + 1
	x - 1

و (C) المنحنى الممثل لها في معلم متعامد ممنظم
(O ; i^→ ; j^→)
1) حدد D مجموعة تعريف الدالة f
2) احسب النهايات التالية

lim - ∞

f(x)

lim + ∞

f(x)

lim 1-

f(x)

lim 1+

f(x)

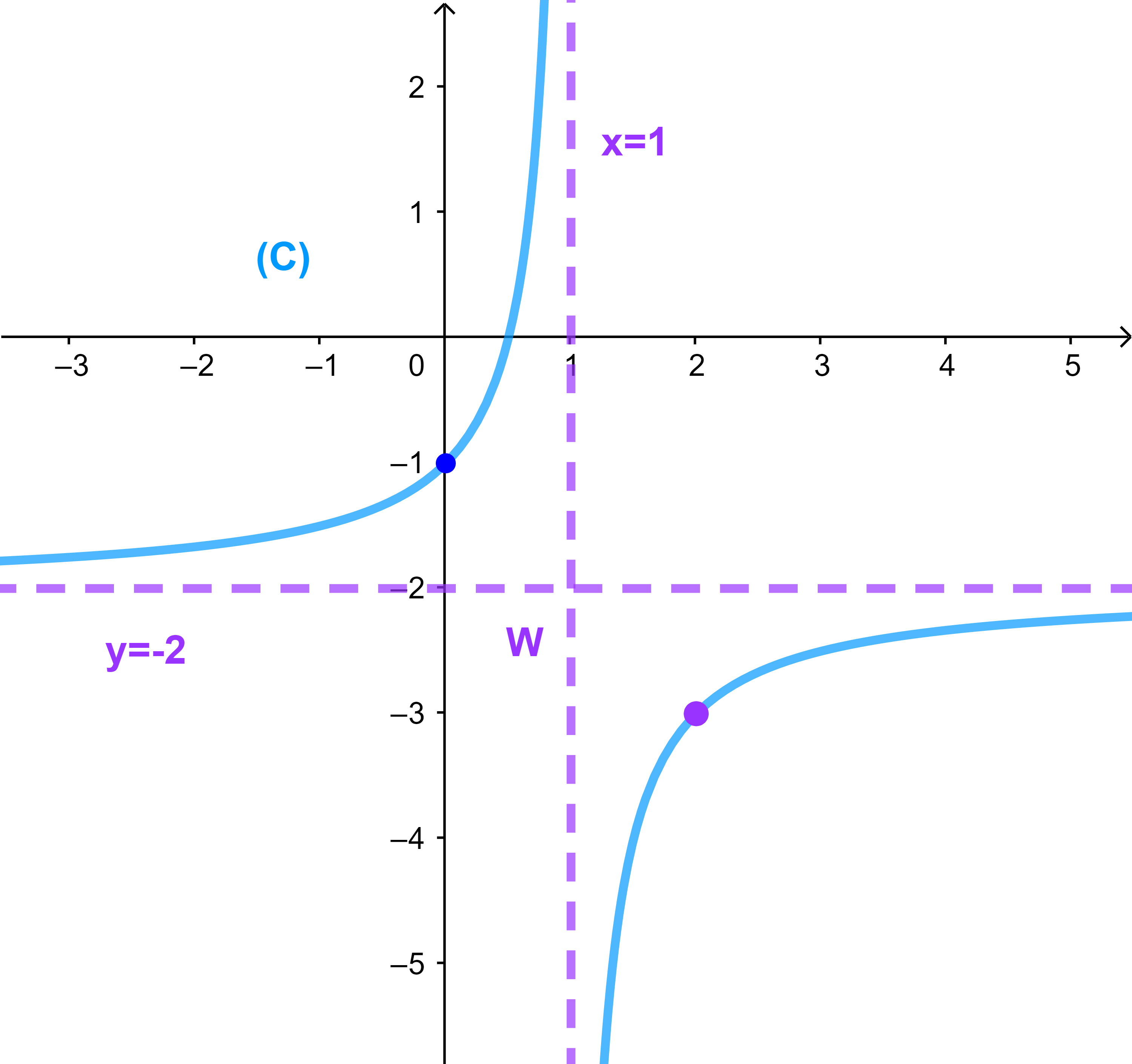
3) استنتج مقاربات المنحنى (C)

تصحيح

1) الدالة f معرفة اذا كان x - 1 ≠ 0 أي x ≠ 1
ومنه فان D = ]-∞ ; 1[ ∪ ]1 ; +∞[
2) النهايات
ندرس حالتين 1^- و 1⁺
نضع p(x) = -2x + 1 و q(x) = x - 1
لدينا p(1) = -2(1) + 1 = -1
ولدينا q(1) = 1 - 1 = 0

لدراسة نهاية الدالة f في 1 ندرس اشارة المقام x - 1

x		-∞		1		+∞
x - 1			-	0	+

عندما x → 1^- فان q(x) → 0^-

lim 1-	f(x) =	lim 1-	-2x + 1
			x - 1

-1	= + ∞	لدينا
0-

lim 1-

f(x) = +∞

اذن

عندما x → 1⁺ فان q(x) → 0⁺

-1	= - ∞	لدينا
0+

lim 1+

f(x) = - ∞

اذن

lim -∞	f(x) =	lim -∞	- 2x	= -2
			x

lim +∞	f(x) =	lim +∞	- 2x	= -2
			x

3) المقاربات
للتذكير لتحديد المقاربات لمنحنى دالة عددية ينبغي معرفة محدات مجموعة تعريف هذه الدالة
توجد أربع محدات

1-		1+
- ∞		+ ∞

lim 1-

f(x) = +∞

لدينا

اذن المستقيم (D): x = 1 مقارب ل (C)

lim 1-

f(x) = +∞

ولدينا كذلك

اذن المستقيم (D): x = 1 مقارب ل (C)

lim -∞

f(x) = -2

لدينا

اذن المستقيم (D'): y = -2 مقارب ل (C) بجوار -∞

lim +∞

f(x) = -2

ولدينا كذلك

اذن المستقيم (D'): y = -2 مقارب ل (C) بجوار +∞