Exercice 1 tp

Soit f une fonction numérique définie par

f(x) =	-2x + 1
	x - 1

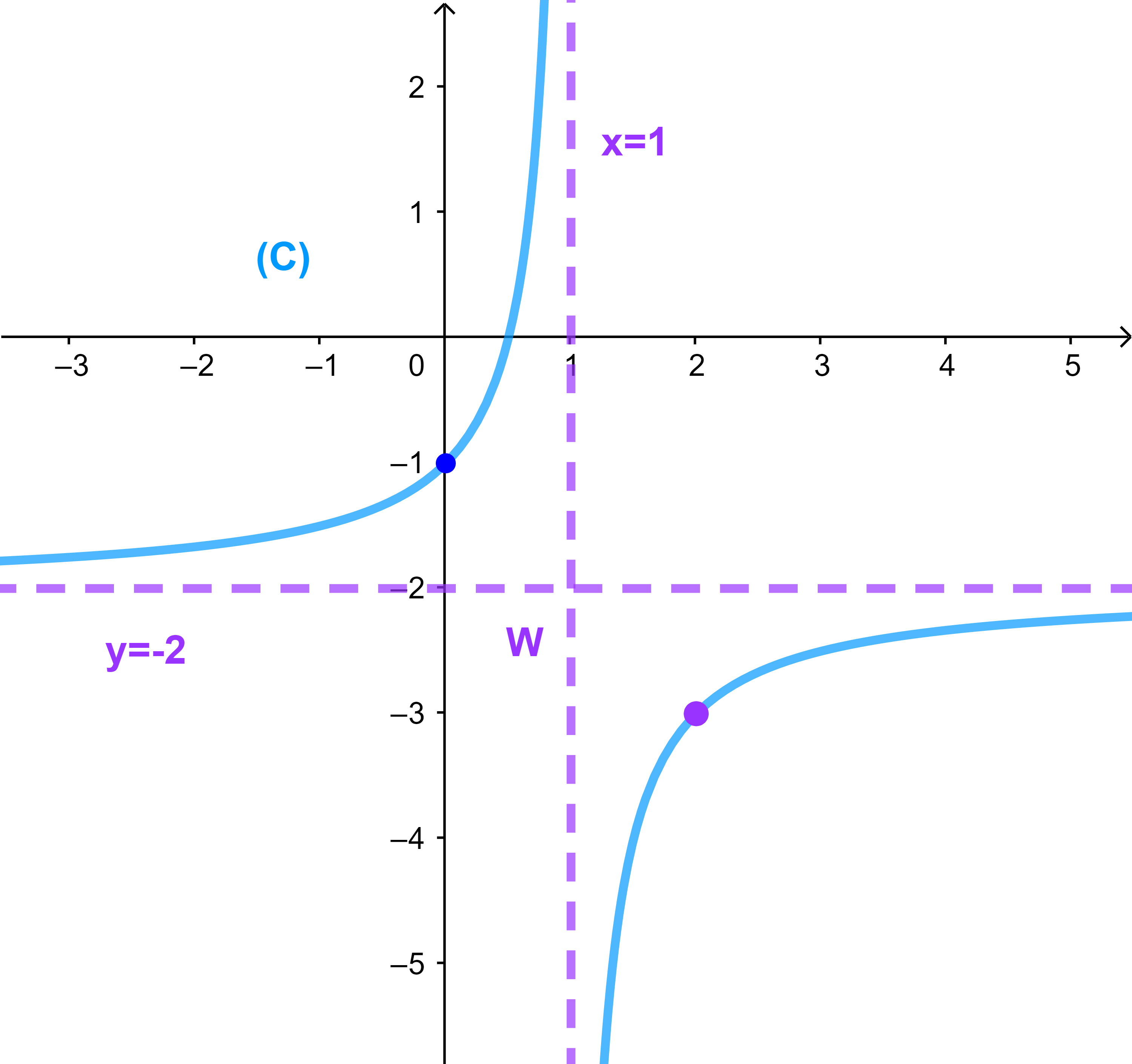
et (C) sa courbe représentative dans un repère orthonormé (O ; i^→ ; j^→)
1) Déterminer D ensemble de définition de f
2) Calculer les limites suivantes

lim 1-

f(x)

lim 1+

f(x)

lim -∞

f(x)

lim +∞

f(x)

3) Déduire les asymptotes de la courbe (C)

Correction

1) f est définie si x-1≠ 0 ou encore si x≠1
donc D = ]-∞ ; 1[∪]1 ; +∞[

2) Limite de f en 1^- et 1⁺

On pose p(x) = -2x + 1 et q(x) = x - 1
p(1) = -2(1) + 1 = -1 et q(1) = 1 - 1 = 0

Pour déterminer la limite au point 1 on étudie d'abord le signe de x - 1

x		-∞		1		+∞
x - 1			-	0	+

1) Si x → 1^- alors q(x) → 0^-

lim 1-	f(x) =	lim 1-	-2x + 1
			x - 1

On a

-1	= + ∞
0-

donc

lim 1-

f(x) = +∞

2) Si x → 1⁺ alors q(x) → 0⁺

-1	= - ∞	Donc	lim 1+	f(x) = - ∞
0+

LImite de f en -∞ et +∞

lim -∞	f(x) =	lim -∞	- 2x	= -2
			x

lim +∞	f(x) =	lim +∞	- 2x	= -2
			x

3) Rappel Pour déterminer les asymptotes de (C) on doit connaitres les bord de D

1-		1+
- ∞		+ ∞

Il y a quatre bords pour D

On a

lim 1-

f(x) = +∞

Donc la droite (D): x = 1 est asymptote à (C) à gauche à 1

Et on a également

lim 1+

f(x) = - ∞

Donc la droite (D): x = 1 est asymptote à (C) à droite à 1

On a

lim -∞

f(x) = -2

Donc la droite (D'): y = -2 est asymptote à (C) au voisinage de -∞

Et on a également

lim +∞

f(x) = -2

Donc la droite (D'): y = -2 est asymptote à (C) au voisinage de +∞