Etude des fonctions (5)
Exercice 1 tp
Soit f une fonction numérique définie par
f(x) = -x² + 4x et
(C) sa courbe dans un repère orthonormé (O;i→;j→)
1) Déterminer D ensemble de définition de f
2) Calculer les deux limites suivantes
lim - ∞ |
f(x) | lim + ∞ |
f(x) |
3) (a) Calculer f '(x) tel que x∈D et étudier la monotonie de f
(b) Tracer le tableau de variations de f et déduire son extremum
4) (a) Tracer (C)
(b) Résoudre graphiquement l'équation f(x) = 0
(c) Résoudre graphiquement
l'inéquation f(x) ≤ 0
(d) Résoudre graphiquement le système
de deux inéquations 3 ≤ f(x) ≤ 4
Correction
1) f est un polynôme donc D = IR
2) Calcul des limites
lim - ∞ |
f(x) | = | lim - ∞ |
-x² = - ∞ |
lim + ∞ |
f(x) | = | lim + ∞ |
-x² = - ∞ |
3) (a) f est un polynôme donc dérivable sur IR
Soit x∈IR
f '(x) = (-x² + 4x)' = -x + 4
Donc pour tout (x∈IR) on a f '(x) = -x + 4
Signe de f '(x)
f'(x) = 0 ⇔ -2x + 4 = 0
⇔ -2x = -4 ⇔ x=2
f '(x) est de la forme ax+b
a = -2 > 0 donc
| x | -∞ | 2 | +∞ | |||
| -2x + 4 | + | 0 | - |
Si x∈]-∞ ; 2[ alors f '(x) > 0
Si x∈]2 ; +∞[ alors f '(x) < 0
Donc f est strictement croissante
sur ]-∞ ; 2] et strictement décroissante
sur [2 ; +∞[
(b) Tableau de variations de f
| x | -∞ | 2 | +∞ | |||
| f '(x) | + | 0 | - | |||
| f | -∞ | ↗ | 4 | ↘ | -∞ |
f ' s'annule en 2 et change de signe de (+) à (-) donc f(2)=4 est une valeur maximale de f
4) (a) La courbe (C
Pour tracer la courbe (C), il suffit de sélectionner quelques images des abscisses convenables
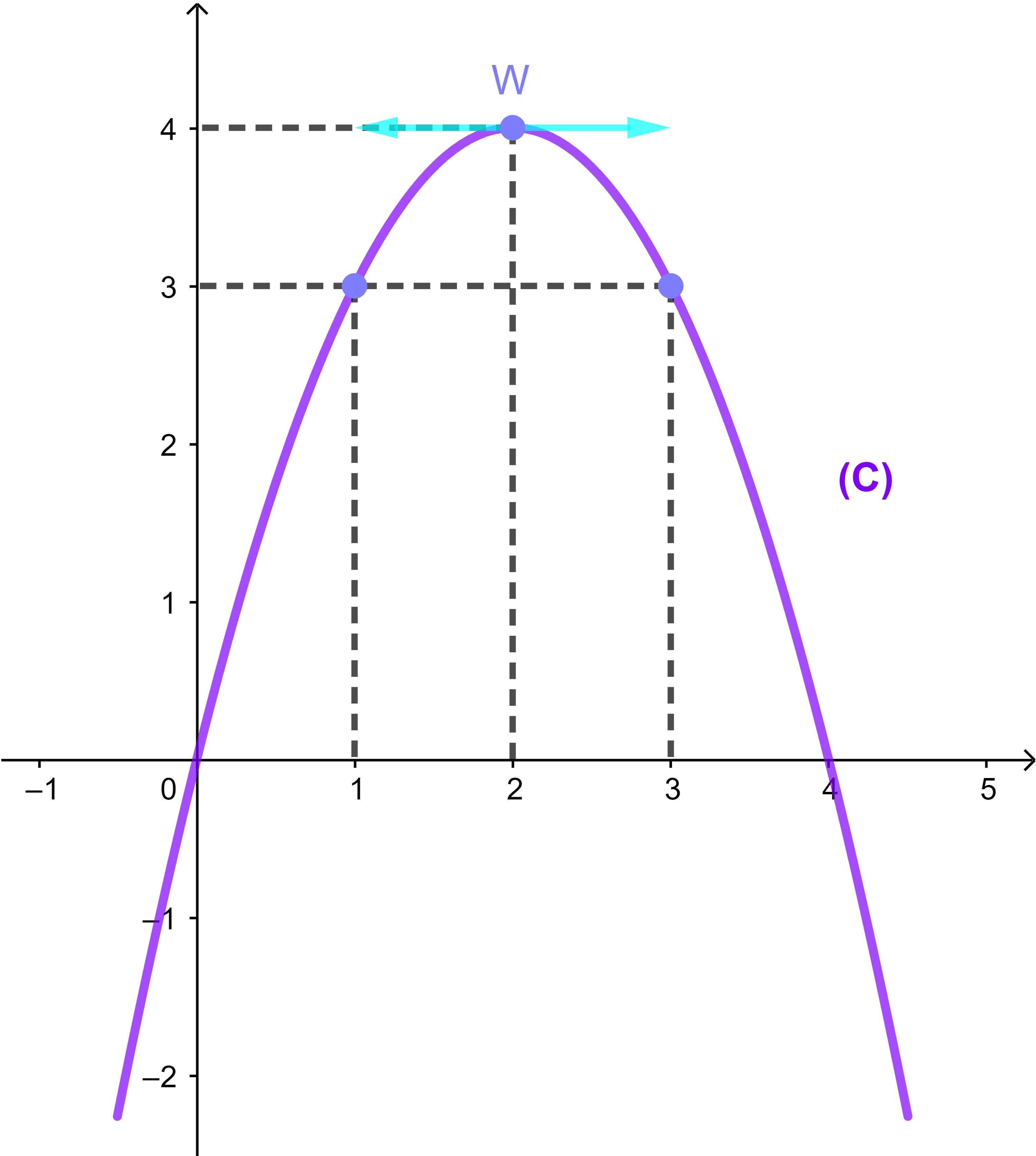
(b) Equation f(x) = 0: il suffit de donner les abscisses des points d'intérsection de la courbe avec l'axe des abscisses (Ox)
La courbe (C) coupe l'axes des abscisses en deux points donc l'équation admet deux solutions a=0 et b=4
(c) Inéquation f(x) ≤ 0
Il suffit de donner les intervalles ou la courbe est au dessous de l'axe des abscisses
Dans les deux intervalles ]-∞ ; 0] et [4 ; +∞[ la courbe (C) est au dessous de l'axe (Ox) donc l'ensemble de solutions de l'inéquation f(x) ≤ 0
S = ]-∞ ; 0] ∪ [4 ; +∞[
(d) Système de deux inéquations
3 ≤ f(x) ≤ 4
Il suffit de donner les intervalles ou la courbe est entre les deux droites
(D): y=3 et (D'): y=4
Remarque f(1)=3 ; f(2)=4 ; f(3)=3
Si on projete le petit moeceau de la parabole entre (D) et (D') on obtient un segment représenté par l'intervalle [1 ; 3]
Ainsi S3 = [1 ; 3]