(6) التمثيل المبياني لدالة
تمرين 1 tp
لتكن f دالة عددية معرفة كما يلي
| f(x) = | 2x - 1 |
| x - 1 |
و (C) المنحنى الممثل لها في معلم متعامد ممنظم
(O ; i→ ; j→)
1) حدد D مجموعة تعربف الدالة f
2) احسب النهايات التالية
lim - ∞ |
f(x) | lim + ∞ |
f(x) | |
lim 1- |
f(x) | lim 1+ |
f(x) |
واستنتج مقاربات المنحنى (C)
3) احسب f'(x) حيث x∈D وادرس رتابة الدالة f وانشئ جدول تغيراتها
4) انشئ المقاربين والمنحنى (C)
تصحيح
1) f معرفة اذا كان x-1 ≠ 0 أي x ≠ 1
اذن
D = IR\{1} = ]-∞ ; 1[ ∪ ]1 ; +∞[
2) حساب النهايات وتحديد المقاربات
lim -∞ | f(x) = | lim -∞ | 2x | = 2 |
| x |
وهذا يعني أن المنحنى (C) يقبل مقاربا
معادلته y = 2 بجوار -∞
lim +∞ | f(x) = | lim +∞ | 2x | = 2 |
| x |
وهذا يعني أن المنحنى (C) يقبل مقاربا
معادلته y = 2 بجوار +∞
2) i3. لتحديد النهاية على اليمين او على اليسار
ندرس اشارة المقام x - 1
باستعمال جدول الاشارة بجوار النقطة 1
نضع p(x) = 2x - 1 و q(x) = x - 1
لدينا p(1) = 2(1) - 1 = 1
| x | -∞ | 1 | +∞ | |||
| x - 1 | - | || | + |
عندما x → 1- فان q(x) → 0-
lim 1- |
f(x) | = | 1 | = - ∞ |
| 0- |
ومنه فان المستقيم (D): x = 1 مقارب ل (C)
عندما x → 1+ فان q(x) → 0+
lim 1+ |
f(x) | = | 1 | = + ∞ |
| 0+ |
ومنه فان المستقيم (D): x = 1 مقارب ل (C)
4) f دالة جذرية اذن قابلة للاشتقاق على D ولدينا لكل x∈D
| f '(x) = | (2x-1)'(x-1) - (2x-1)(x-1)' |
| (x-1)² | |
| = | 2(x-1) - (2x-1)(1) |
| (x-1)² | |
| = | 2x - 2 - 2x + 1 |
| (x-1)² |
| f ' (x) = | -1 |
| (x - 1)² |
اشارة f '(x)
لدينا -1 < 0 و (x-1)² > 0
اذن (∀x∈IR \{1}) f '(x) < 0
وهذا يعني ان الدالة f تناقصية قطعا على ]-∞ ; 1[ وتناقصية قطعا كذلك على ]1 ; +∞[
جدول تغيرات الدالة f
| x | -∞ | 1 | +∞ | |||||
| f '(x) | - | || | - | |||||
| f | 2 | ↘ | -∞ | || | +∞ | ↘ | 2 |
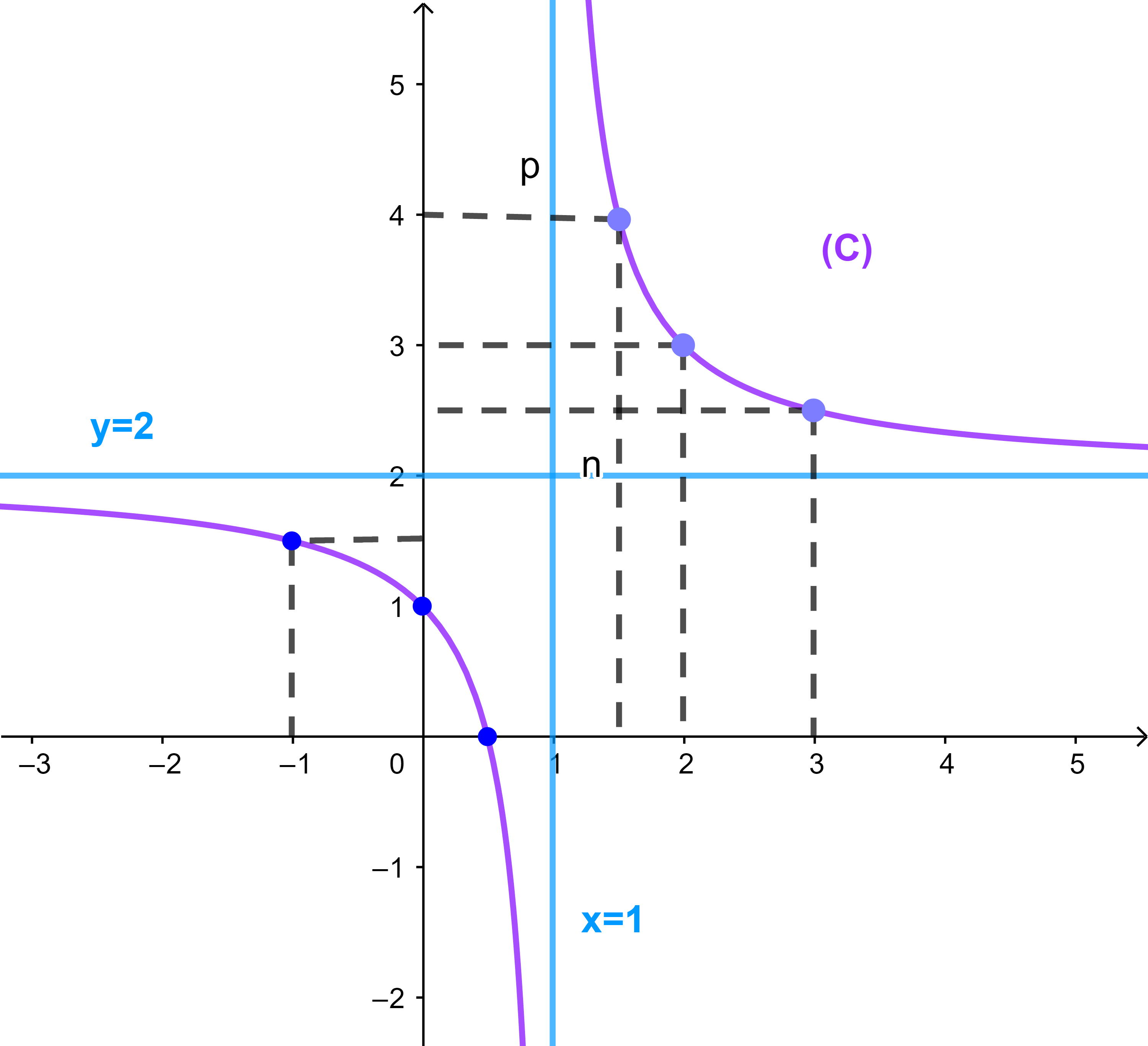
5) منحنى الدالة f
لرسم المنحنى (C) يكفي تعيين قيم افاصيل مناسبة لبعض نقط المنحنى