Exercice 1 tp

Soit f une fonction numérique définie par
f(x)= x³ - 3x + 1
et C) sa courbe dans un repère orthonormé
(O;i^→;j^→)
Déterminer D ensemble de définition de f 2) Calculer les deux limites suivantes

lim - ∞

f(x)

lim + ∞

f(x)

3) Calculer f '(x) tel que x∈D
4) Etudier les variations de f et déduire son extremum

5) (a) Tracer (C)
(b) Résoudre graphiquement l'équation f(x) = 0
(c) Résoudre graphiquement l'équation f(x) = m selon les valeurs de m∈IR

Correction

1) f est un polynôme donc D = IR
2) Limites

lim - ∞	f(x)	=	lim - ∞	x³ = - ∞
lim + ∞	f(x)	=	lim + ∞	x³ = + ∞

3) f est un polynome donc dérivable sur IR
Soit x∈IR
f '(x) = (x³ -3x + 1)' = 3x² - 3
donc pour tout x∈IR on a f '(x) = 3x² - 3
4) Signe de f '(x)
f '(x) = 0 ⇔ 3x²-3 = 0 ⇔ 3(x²-1) = 0
⇔ x²-1 = 0 ⇔ x² = 1 ⇔
( x = -√1 ou x=√1) ⇔ (x=-1 ou x=1)
f'(x) est un trinôme et on a a=3 > 0

x	-∞		-1		1		+∞
f '(x)		+	0	-	0	+

Si x∈]-∞ ; -1[ alors f '(x) > 0
Si x∈]-1 ; 1[ alors f '(x) < 0
Si x∈]1 ; +∞[ alors f '(x) > 0 Donc f est strictement décroissante sur ]-∞ ; -1] et strictement croissante sur [1 ; +∞[
et strictement décroissante sur [-1 ; 1]
Tableau de variations

x	-∞		-1		1		+∞
f'(x)		+	0	-	0	+
f'	-∞	↗	3	↘	-1	↗	+∞

f ' s'annule en -1 et change de sigbe de (+) à (-) donc f(-1) = 3 est une valeur maximale
f ' s'annule en 1 et change de sigbe de (-) à (+) donc f(1) = -1 est une valeur minimale

5) (a) La courbe (C)

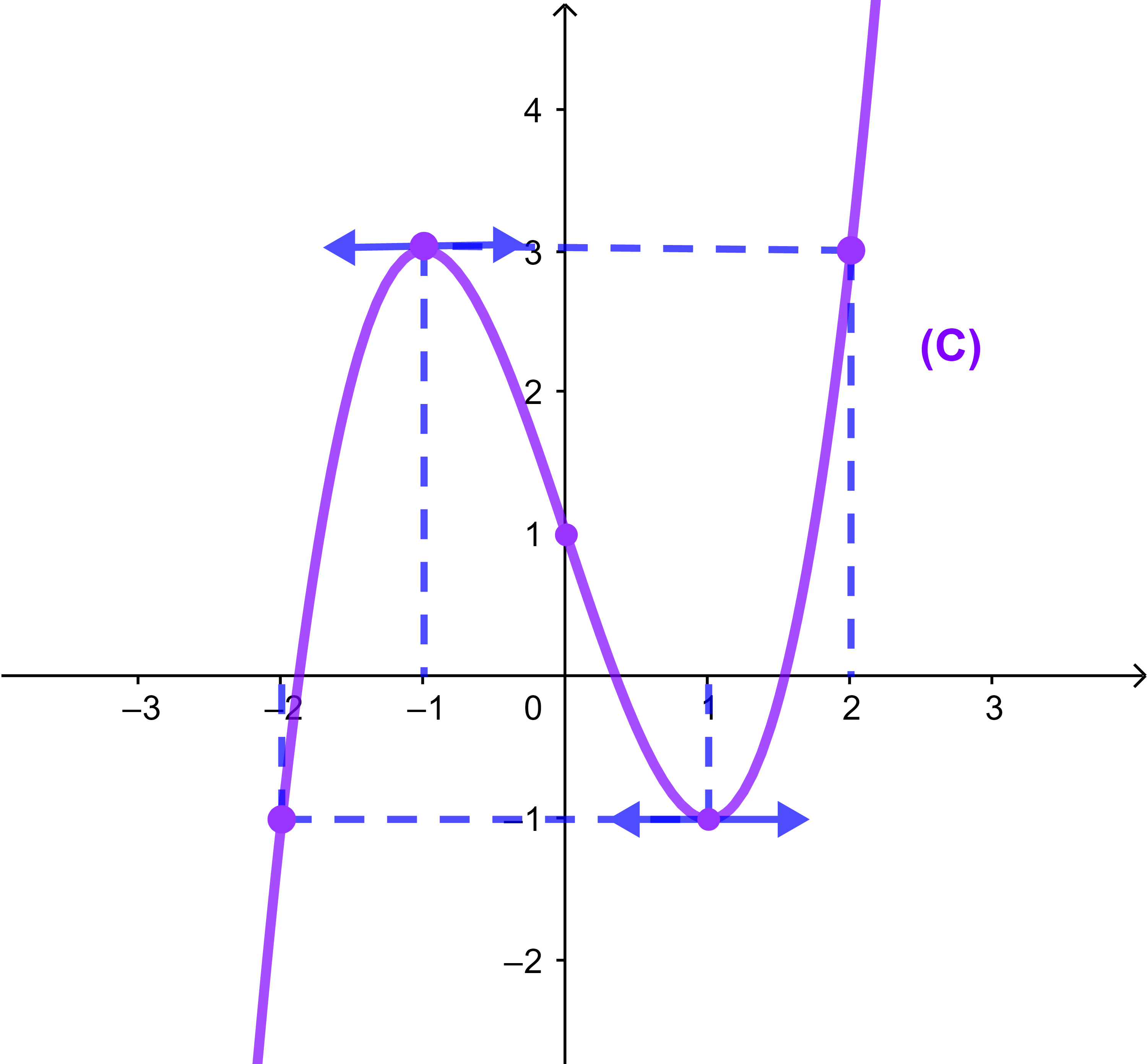
(b) Equation f(x) = 0
Il suffit de donner les abscisses des points d'intérssection de la courbe avec l'axe des abscisses (Ox)
La courbe (C) coupe l'axe des abscisses en trois points d'abscisses réspéctivement a ; b et c
-2 < a < -1 ; < b < 1 ; < c < 2
(c) Equation f(x) = m
On considère les droites (D): y = m ces droites sont parallèles à l'axe des abscisses pour tout m∈IR

Si m < -1 alors (D) coupe (C) en un seul point donc l'équation admet une seul solution
Si m = -1 alors (D) coupe (C) en un deux points donc l'équation admet deux solutions -2 et 1
Si -1 < m < 3 alors (D) coupe (C) en trois points donc l'équation admet trois solutions
Si m = 3 alors (D) coupe (C) en un deux points donc l'équation admet deux solutions -1 et 2
Si m > 3 alors (D) coupe (C) en un seul point donc l'équation admet une seul solution.