(1) عموميات حول الدوال العددية
1- تذكير واضافات
1.1 الدالة العددية والتأويل الهندسي
1.1.1 تعريف دالة عددية
لتكن E و F مجموعتين غير فارغتين من IR.
الدالة العددية
المعرفة من E نحو F هي علاقة نرمز لها بحرف f او (g او h ..) التي تربط كل عنصر x من E بعنصر واحد على الاكثر في F ويسمى ان وجد
صورة x بواسطة الدالة f ونرمز لها ب f(x).
E تسمى مجموعة الانطلاق.
F تسمى مجموعة الوصول.
x يسمى متغير حقيقي ل f.
1.2.2 مجموعة تعريف دالة
لتكن f دالة عددية لمتغير حقيقي x.
مجموعة تعريف الدالة f
هي مجموعة الاعداد الحقيقية التي لها صورة بواسطة f ونرمز لها ب Df أو D.
x∈Df يعني f(x)∈IR.
تمرين 1 tp
لتكن f دالة عددية لمتغير حقيقي x ومعرفة كما يلي
| f(x) = | 1 |
| x-3 |
حدد مجموعة تعريف الدالة f.
تصحيح
1) نلاحظ ان f(x) هي مقلوب ل x-3 وتسمى دالة كسرية واأيضا دالة جذرية
اذن العدد x-3 ليس له مقلوبا اذا كان منعدما اي اذا كان
x-3=0
أي
x=3
ومنه فان العدد
3 ليس له صورة ب f.
وبالتالي
D=IR\{3}.
وأيضا
D=]-∞;3[∪]3;+∞[.
تمرين 2 tp
لتكن f دالة عددية لمتغير حقيقي x ومعرفة كما يلي
| f(x) = | 1 |
| x² - 3x - 10 |
حدد مجموعة تعريف الدالة f.
تصحيح
1) نلاحظ ان f(x) هي مقلوب ل x²-3x-10 وتسمى دالة كسرية وأيضا دالة جذرية.
اذن العدد x²-3x-10 يكون ليس له مقلوبا اذا كان منعدما اي اذا كان x²-3x-10=0 وهذه معادلة من الرتبة 2.
| a = 1 | b = -3 | c = -10 |
Δ=b²-4ac=(-3)²-4.1.(-10)=9+40
Δ=49>0 اذن المعادلة تقبل حلين مختلفين.
| x1 = | -b - √(Δ) | x2 = | - b + √(Δ) | |
| 2a | 2a | |||
| = | -(-3) - √(49) | = | -(-3) + √(49) | |
| 2.1 | 2.1 |
| x1 = | 3-7 | x2 = | 3+7 | |
| 2 | 2 | |||
| = | -2 | = | 5 |
اذن
D=IR\{-2;5}.
وأيضا D=]-∞;-2[∪]-2;5[∪]5;+∞[.
الدالة الحدودية من الدرجة الثانية
الدالة العددية لمتغير حقيقي x التي تكتب على الشكل
f(x)=ax²+bx+c تسمى دالة حدودية من الدرجة الثانية ومجموعة تعريفها IR.
1.1.3 التمثيل المبياني لدالة عددية
المستوى منسوب الى معلم متعامد ممنظم (O ; i→ ; j→).
لتكن f دالة عددية لمتغير حقيقي x.
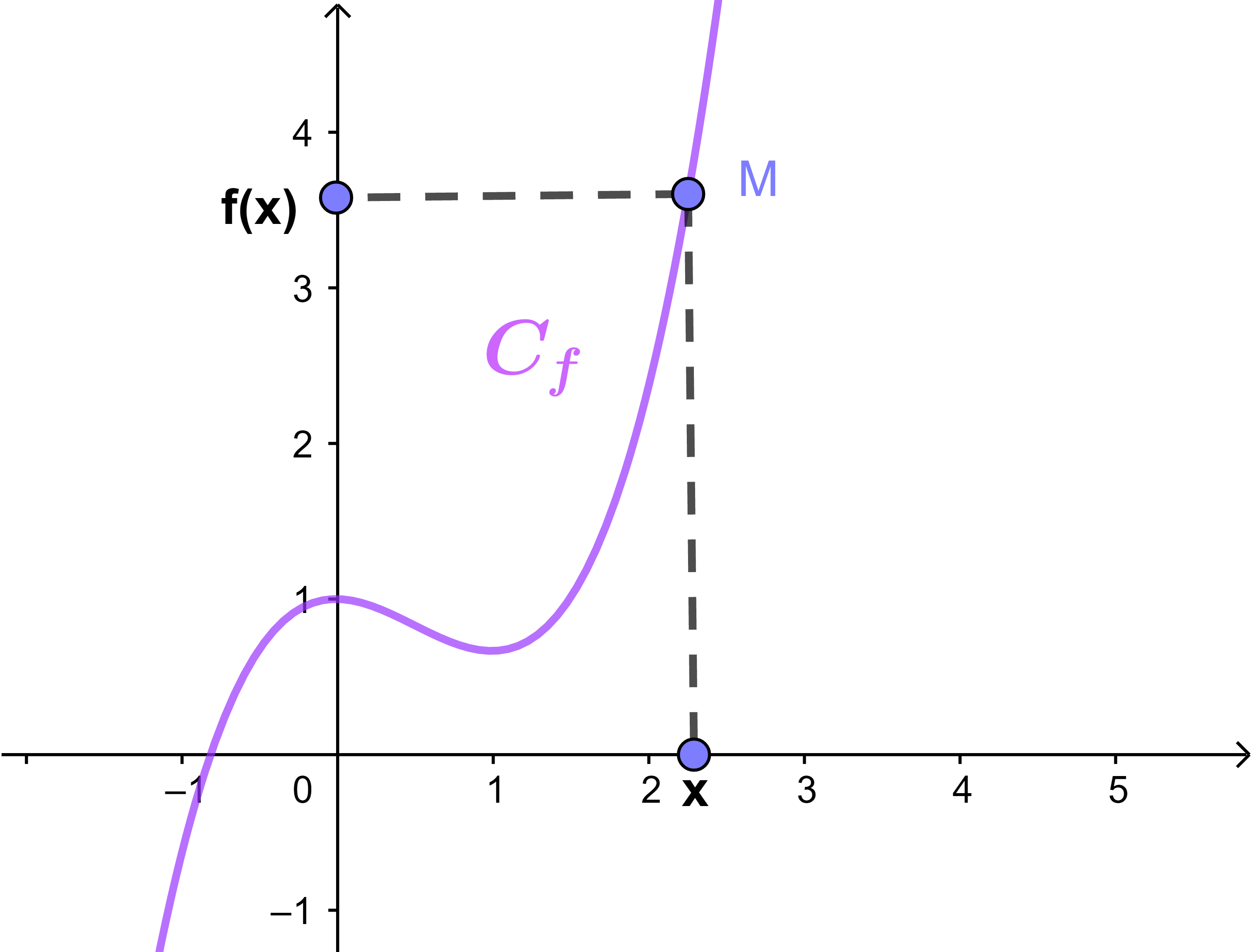
مجموعة النقط M(x;y)
من المستوى بحيث
x∈Df
و y=f(x) تسمى منحنى الدالة f ونرمز له ب Cf أو (C).
M(x;y)∈Cf يعني x∈Df و y=f(x).
للتذكير عند رسم منحنى
1) ننشئ المعلم (غالبا ما يكون متعامدا ممنظما ).
2) نحدد بعض الصور المناسبة في جدول.
3) ربط هذه النقط يعود الى طبيعة الدالة.