1.1.4 تساوي دالتين عدديتين

لتكن f و g دالتين عدديتين و D_f و D_g مجموعتي تعريفهما على التوالي.
نقول ان f و g متساويتان ونكتب f=g
اذا كان D_f=D_g و f(x)=g(x) لكل x∈D
حيث (D=D_f=D_g).

مثال لتكن f و g دالتين عدديتين معرفتين كما يلي

f(x) = x + 1		g(x) =	x² - 2x + 1
			x-1

قارن f و g ?

تصحيح
(a) f دالة تآلفية اذن D_f=IR.
(b) g معرفة اذا كان x-1≠0 أي اذا كان x≠1
اذن D_g=IR\{1}.
بما ان الشرط D_f=D_g لم يتحقق فان f≠g.
(c) ملاحظة اذا كان x≠1 فانه يمكن الاختزال ب x-1.

g(x) =	x²-2x+1	=	(x-1)²	= x - 1
	x-1		x-1

اذن (∀x∈IR\{1})(f(x)=g(x)).

1.2 الدالة الزوجية والدالة الفردية

1.2.1 تعريف

نقول ان مجموعة E مماثلة بالنسبة للصفر اذا كان
لكل x∈E لدينا (-x)∈E

أمثلة

المجموعات التالية مماثلة بالنسبة ل 0
E={-3;-2;0;2;3} و G=[-5;5]
و H=]-7;-4[U]4;7[.

1.2.2 الدالة الزوجية

لتكن f دالة عددية لمتغير حقيقي x و D مجموعة تعريفها.
نقول ان f دالة زوجية اذا تحقق ما يلي
1) لكل x∈D فان -x∈D.
2) لكل x∈D فان f(-x)=f(x).

ملاحظة
نفترض ان f دالة زوجية
اذا كان x∈D فان مقابله ايضا ينتمي الى D
وبالاضافة الى ذلك لهما نفس الصورة بواسطة الدالة f
اي (f(-x)=f(x)).

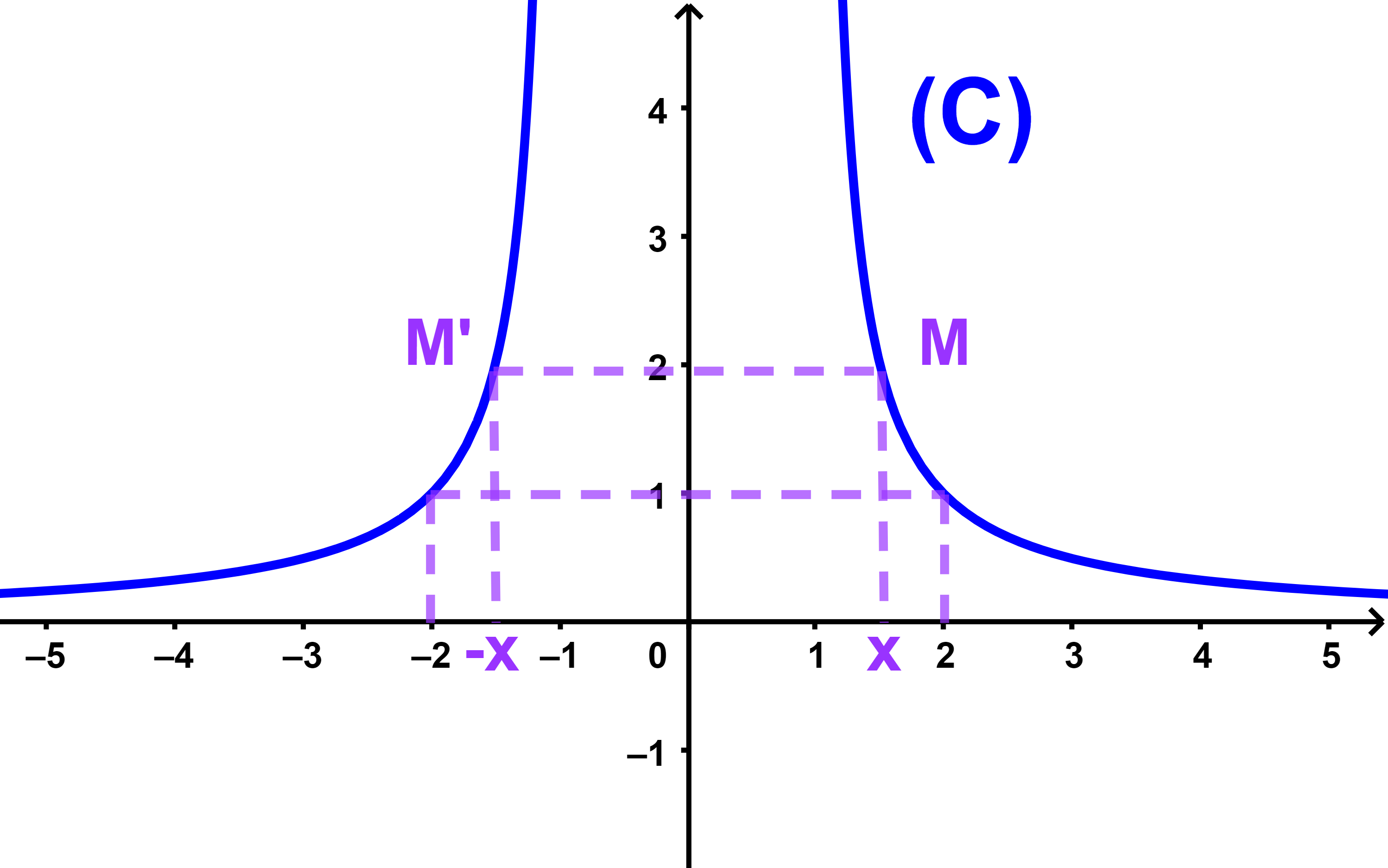
التأويل الهندسي لدالة زوجية
لتكن f دالة زوجية و C_f منحناها الممثل في المعلم
(O;i^→;j^→).
بما ان f(-x)=f(x) حيث x∈IR فان النقطتين M(x;f(x)) و M'(-x;f(x)) مماثلثان بالنسبة لمحور الاراتيب.

نتيجة منحنى دالة زوجية مماثل بالنسبة لمحور الاراتيب.

مثال
نعتبر f دالة عددية لمتغير حقيقي x بحيث
f(x)=x²+5.
بين أن f دالة زوجية.

تصحيح
لكل x∈IR لدينا x²+5∈IR
اذن مجموعة تعريف الدالة f
D_f=IR.

لدينا (∀x∈IR) (-x ∈IR).
ليكن x∈IR.
لدينا f(-x)=(-x)²+5=x²+5=f(x)
اذن f(-x)=f(x) وبالتالي f دالة زوجية.