1- Rappel et compléments

1.1 Fonction numérique et représentation graphique

1.1.1 Définition

Soient E et F deux ensembles non nuls dans IR.
Une fonction numérique f définie de E vers F est une relation qui lie chaque élément x de E par un élément au plus de F, appelé s'il existe image de x par f.

E est appelé ensemble de départ.
F est appelé ensemble d'arrivé.
x est appele variable réel de la fonction f et f(x) son image.

1.1.2 Ensemble de définition d'une fonction

Soit f une fonction numérique de la variable x.
L'ensemble des nombres réels qui admettent une image par f est appelé ensemble de définition de f, noté D_f ou D.

Notons que x∈D ⇔ f(x)∈IR.

Exercice 1 tp

Soit f une fonction numérique définie par

f(x) =	1
	x-3

Déterminer l'ensemble de définition de f.

Correction

f est appelée fonction rationnelle donc elle est définie si son dénominateur est non nul.
x-3=0 ⇔ x=3.

3 n'admet pas d'image par f
ainsi D=IR\{3}=]-∞;3[∪]3;+∞[.

Exercice 2 tp

Soit f une fonction numérique définie par

f(x) =	1
	x² - 3x - 10

Déterminer l'ensemble de définition de f.

Correction

f est une fonction rationnelle donc elle est définie si son dénominateur est non nul.

On résout donc l'équation
x²-3x-10=0.

a = 1

b = -3

c = -10

Δ=b²-4ac=(-3)²-4.1.(-10)=9+40.
Δ=49>0 donc l'équation admet deux solutions différentes

x1 =	-b - √(Δ)		x2 =	- b + √(Δ)
	2a			2a
=	-(-3) - √(49)		=	-(-3) + √(25)
	2.1			2.1

=	3-7		=	3+7
	2			2
=	-2		=	5

donc D=IR\{-2;5}=]-∞;-2[∪]-2;5[∪]5;+∞[.

Fonction polynôme du second ordre
La fonction numérique f de la variable x qui s'écrit sous la forme f(x)=ax²+bx+c tel que a≠0 est appelée fonction polynôme du second ordre et D=IR.

1.1.3 Interprétation graphique d'une fonction

Le plan est rapporté à un repère orthonormé
(O;i^→;j^→).
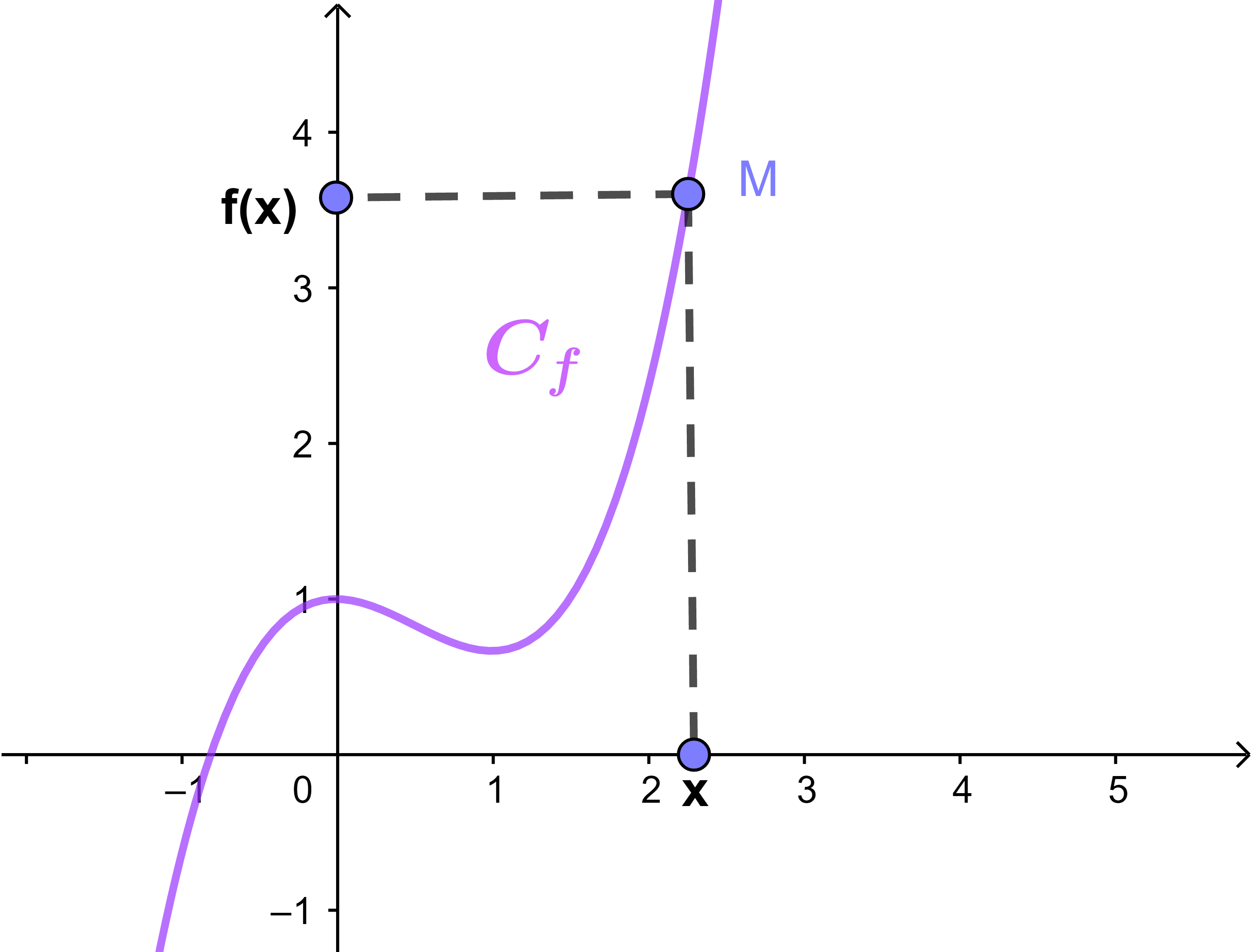
Soit f une fonction numérique et D son ensemble de définition.
L'ensemble des points M(x;f(x)) du plan tels que x∈D et y=f(x) est appelé courbe représentative de la fonction f, notée (C_f) ou (C).