1.1.4 Egalité de deux fonctions

Soient f et g deux fonctions numériques et D_f et D_g respectivement leurs ensembles de définitions.
f et g sont égales et on écrit f=g si les conditions suivantes sont vérifiées
1) D_f=D_g.
2) ∀x∈D on a f(x)=g(x)
tel que (D=D_f=D_g).

Exemple
Soient f et g deux fonctions numériques définies par

f(x) = x + 1		g(x) =	x² - 2x + 1
			x-1

f est une fonction polynôme donc D_f=IR.
g est définie si x-1≠0.
x-1=0 signifie x=1 donc D_g=IR\{1}.
Puisque D_f≠D_g alors f≠g.

Remarque

1.2 Parité d'une fonction

1.2.1 Domaine centré

Soit E une partie de IR.
On dit que E est un domaine symétrique par rapport à 0
si pour tout x∈E on a (-x)∈E.

Exemples
Les ensembles suivants sont symétriques par rapport à zéro
E={-3;-2;0;2;3} ; F=[-5;5]
et G=]-7;-4[U]4;7[.

1.2.2 Fonction paire

Soient f une fonction numérique de la variable réel x et D son domaine de définition.
On dit que f est une fonction paire si les deux conditions suivantes sont vérifiées
1) Pour tout x∈D on a (-x) ∈D.
2) Pour tout x∈D on a f(-x)=f(x).

Remarque
1) Soit f une fonction paire.
Si x∈D alors son opposé appartient à D
et de plus leurs images par f sont égales (f(-x)=f(x)).

2) Si une fonction f est définie sur un domaine n'est pas centré en 0 alors f n'est pas paire.

Interprétation graphique d'une fonction paire
Soit f une fonction paire et C_f sa courbe représentative dans un repère (O;i^→;j^→).

∀x∈IR on a f(-x)=f(x)
donc M(x;f(x)) et M'(-x;f(x)) sont symétriques par rapport à l'axe des ordonnées.

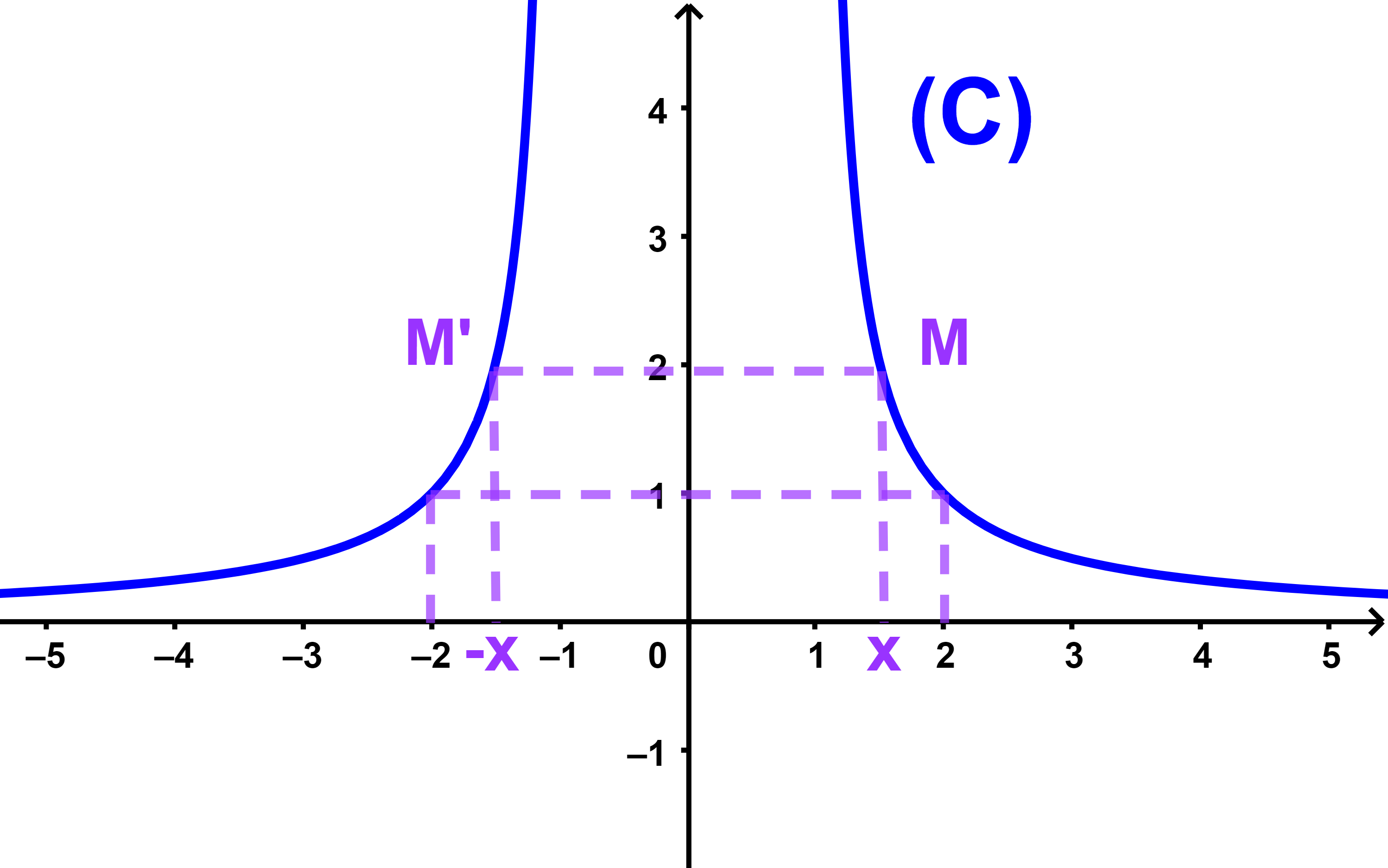
Résultat La courbe représentative d'une fonction paire est symétrique par rapport à l'axe des ordonnées.

Exemple
Soit fune fonction numérique définie par
f(x)=x²+5.
Montrons que f est paire.

1) ∀x∈IR on a x²+5∈IR
donc D_f=IR.
2) IR est centré en 0 donc ∀x∈IR on a (-x) ∈IR.

Soit x∈IR on a f(-x)=(-x)²+5=x²+5
donc f(-x)=f(x) ainsi f est une fonction paire.