Calcul des Limites (1)
Rappel
lim x→+∞ |
x = +∞ | lim x→+∞ |
x³ = +∞ |
lim x→+∞ |
x² = +∞ | lim x→+∞ |
xn = +∞ ; n∈IN* |
Et on a aussi
lim x→0 |
x² = 0 | lim x→0 |
x³ = 0 |
lim x→0 |
xn = 0 | n∈IN* |
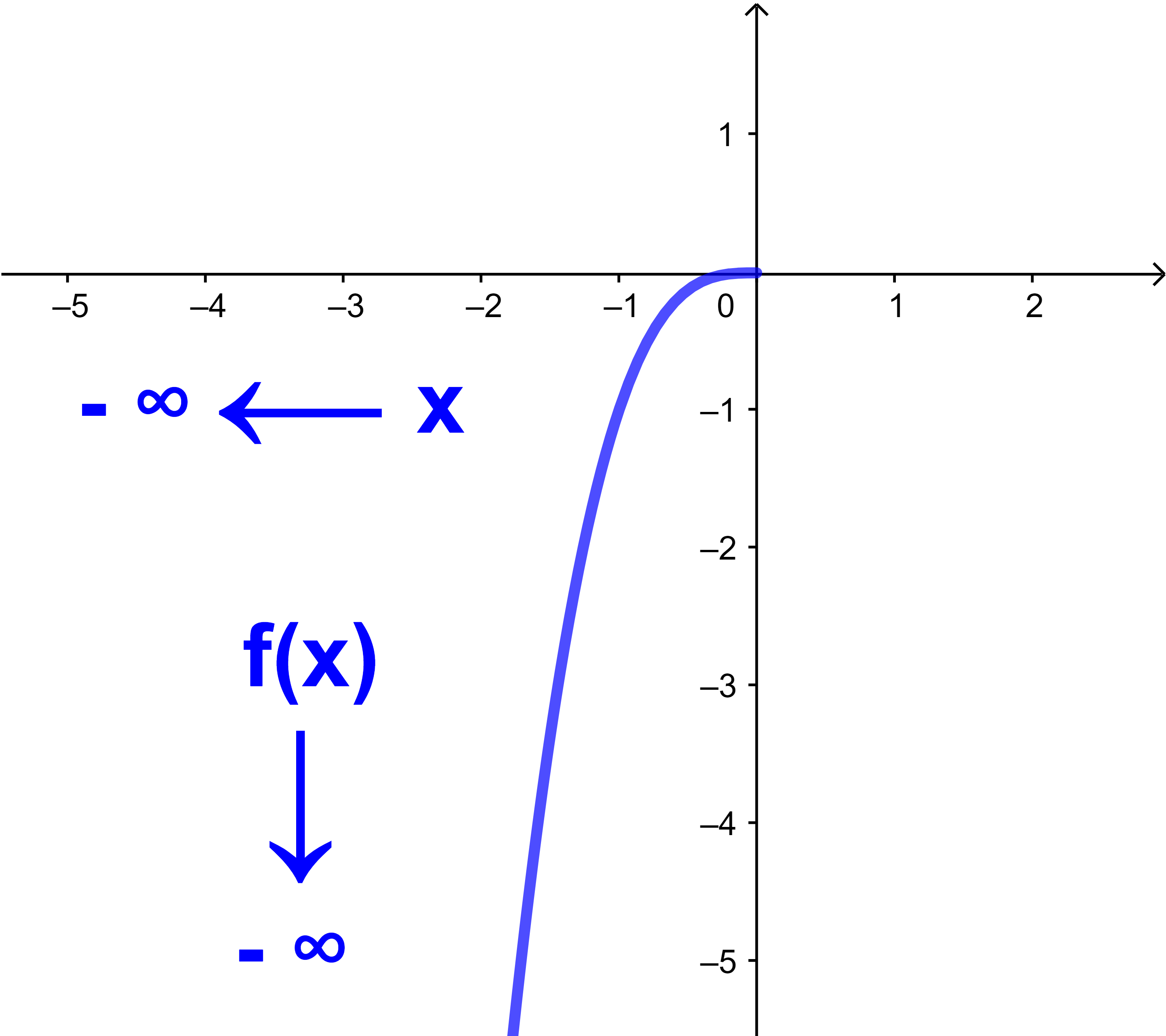
lim x→-∞ |
x³ = -∞ |
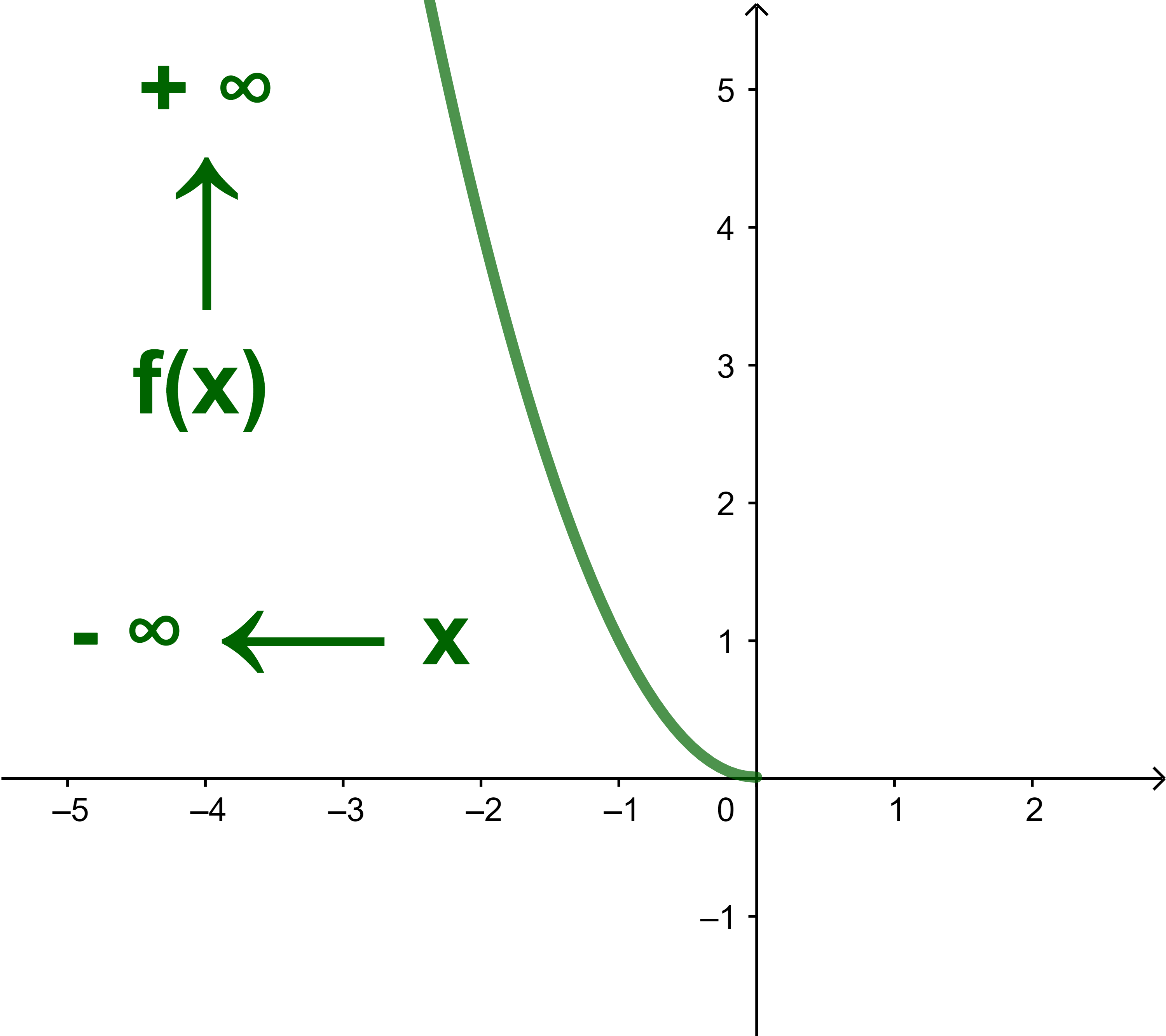
lim x→-∞ |
x² = +∞ |
lim x→-∞ |
x² = +∞ |
lim x→-∞ |
x³ = -∞ |
Si n est pair et non nul
lim x→-∞ |
xn = +∞ |
Si n est impair
lim x→-∞ |
xn = -∞ |
lim +∞ | 1 | = 0 | lim +∞ | 1 | = 0 |
| x | x² |
| n∈IN* | lim +∞ | 1 | = 0 |
| xn |
lim -∞ |
1 | = 0 | et | lim -∞ |
1 | = 0 |
| x | x² |
| n∈IN* | lim -∞ | 1 | = 0 |
| xn |
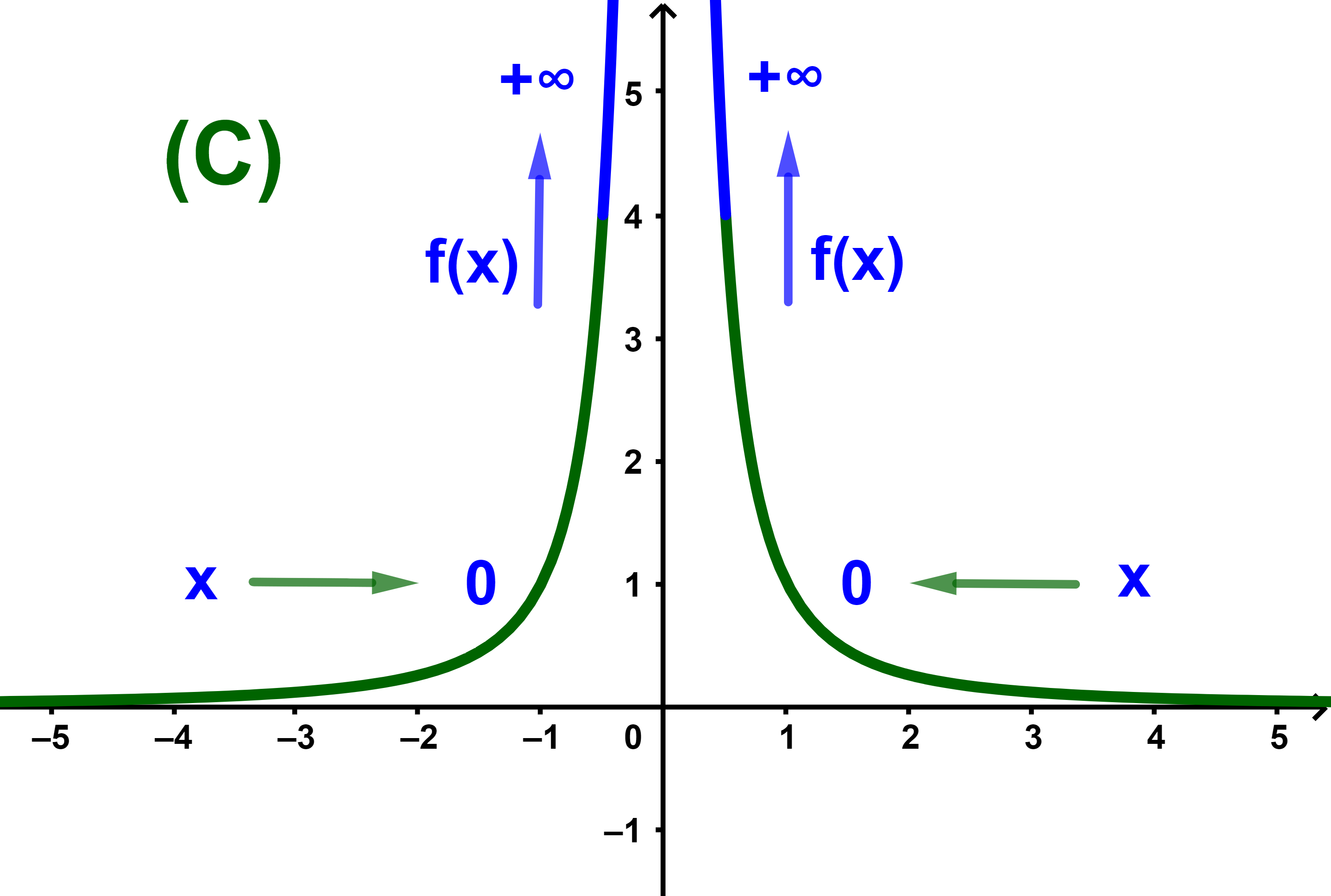
Soit n un entier naturel non nul et pair
lim 0 | 1 | = +∞ | lim 0 | 1 | = +∞ | |
| x² | xn |
p(x) est un polynôme de degré n (axn terme de plus grand degré)
q(x) est un polynôme de degré m (bxm terme de plus grand degré)
lim a | p(x) = p(a) |
lim a | p(x) | = | p(a) | ; q(a)≠0 |
| q(x) | q(a) |
lim +∞ | p(x) = | lim +∞ | (axn) |
lim -∞ | p(x) = | lim -∞ | (axn) |
lim -∞ | p(x) = | lim -∞ | (axn) |
lim +∞ | p(x) | = | lim +∞ | axn |
| q(x) | bxm | |||
lim -∞ | p(x) | = | lim -∞ | axn |
| q(x) | bxm |