(5) مبادئ في المنطق
3- الاستدلالات المنطقية
للتذكير
1) عبارة منطقية تكون اما صحيحة واما خاطئة.
2) عبارة منطقية لا يمكن ان تكون صحيحة وخاطئة في آن واحد.
3) اذا كانت عبارة صحيحة و الاستلزام صحيحا فان العبارة صحيحة ايضا.
عمليا للبرهنة على صحة الاستلزام p⇒q
يكفي ان نفترض ان العبارة p صحيحة ونبين ان العبارة q صحيحية ايضا.
3.1 الاستدلال بالخلف
للبرهنة على صحة عبارة q يكفي اتباع المراحل التالية
1) نفترض ان العبارة q خاطئة
وانطلاقا من هذا الافتراض نصل الى ان العبارة q ونفيها ⌉q صحيحتان معا وهذا غير ممكن.
2) نستنتج اذن ان الافتراض كان خاطئا اي ان العبارة q صحيحة.
مثال
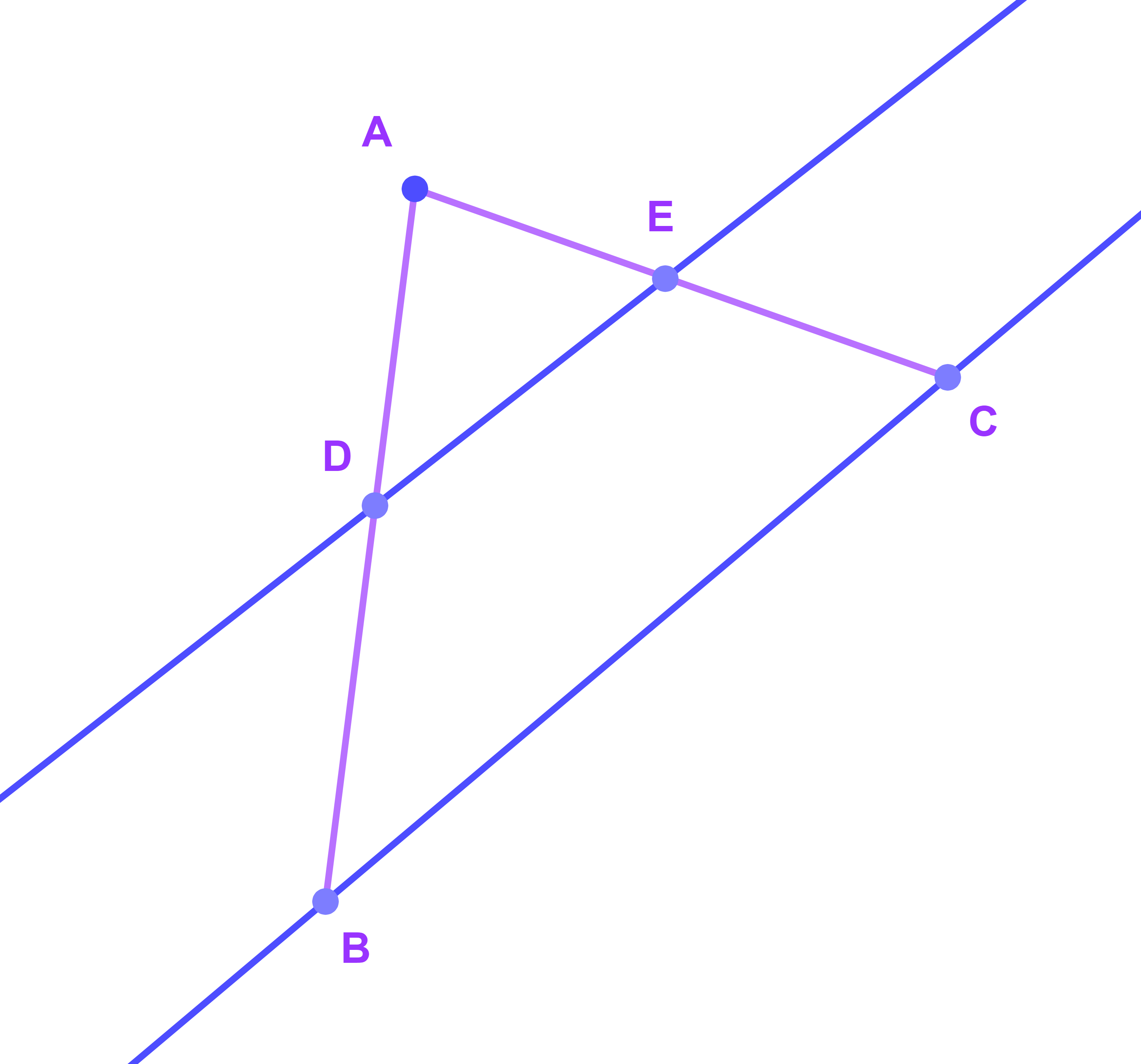
ليكن ABC مثلثا بحيث
AB=5 و BD=3 و CE=2,25 و AC=4,25 و E∈[AC] و D∈[AB].
هل (DE)||(BC) ?
تصحيح
نفترض ان المستقيمين متوازيان
(DE)||(BC)
حسب مبرهنة طاليس
| AB | = | AC | ⇔ | 5,4 | = | 4,25 |
| AD | AE | 3 | 2,25 |
⇔ 5,4×2,25=3×4,25
⇔ 12,15=12,75
وهذا غير ممكن نستنتج اذن ان المستقيمين (DE) و (BC) غير متوازيان.
3.2 الاستدلال بفصل الحالات
لتكن p و q و r عبارات منطقية.
للبرهنة على ان
(p⋁q) ⇒ r
نبين ان
p ⇒ r
صحيحة
وان
q ⇒ r
صحيحة ايضا.
وعمليا تكون
q=⌉p
وللبرهنة على
(p⋁⌉p) ⇒ r
يكفي ان نبين ان
p ⇒ r و ⌉p⇒r.
مثال
حل في
IR
المعادلة
(E): |x-2|=5.
تصحيح
العدد
x-2 يمكن ان يكون سالبا او موجبا
اذن توجد حالتان للمناقشة
اذا كان x-2 موجبا اي x≥2 فان |x-2| = x-2
المعادلة (E) ثصبح x-2=5 اذن x=7.
اذا كان x-2 سالبا اي x≤ 2
فان |x-2|=-(x-2)=-x+2
المعادلة (E) تصبح -x+2=5 اذن x=-3
وبالتالي مجموعة حلول المعادلة (E)
S={-3;7}.