Dérivation et fonctions primitives (14)
2.2 Etude des fonctions de la forme
x→√(ax+b)
2.2.1 La fonction x→ √(x)
Propriétés
1) L'ensemble de définition de la fonction f: x→ √(x) est D=[0;+∞[ et sa limite en +∞ est +∞.
lim +∞ |
f(x) = | lim +∞ |
√(x) = +∞ |
2) f est dérivable sur IR+*=]0;+∞[.
Soit x∈]0;+∞[.
| f'(x) = | 1 |
| 2√(x) |
(∀x∈>0) on a f'(x)>0 donc f est strictement croissante sur ]0;+∞[.
Tableau de variations de f
| x | 0 | +∞ | |
| f'(x) | || | + | |
| f | 0 | ↗ | +∞ |
4) La courbe représentative de f
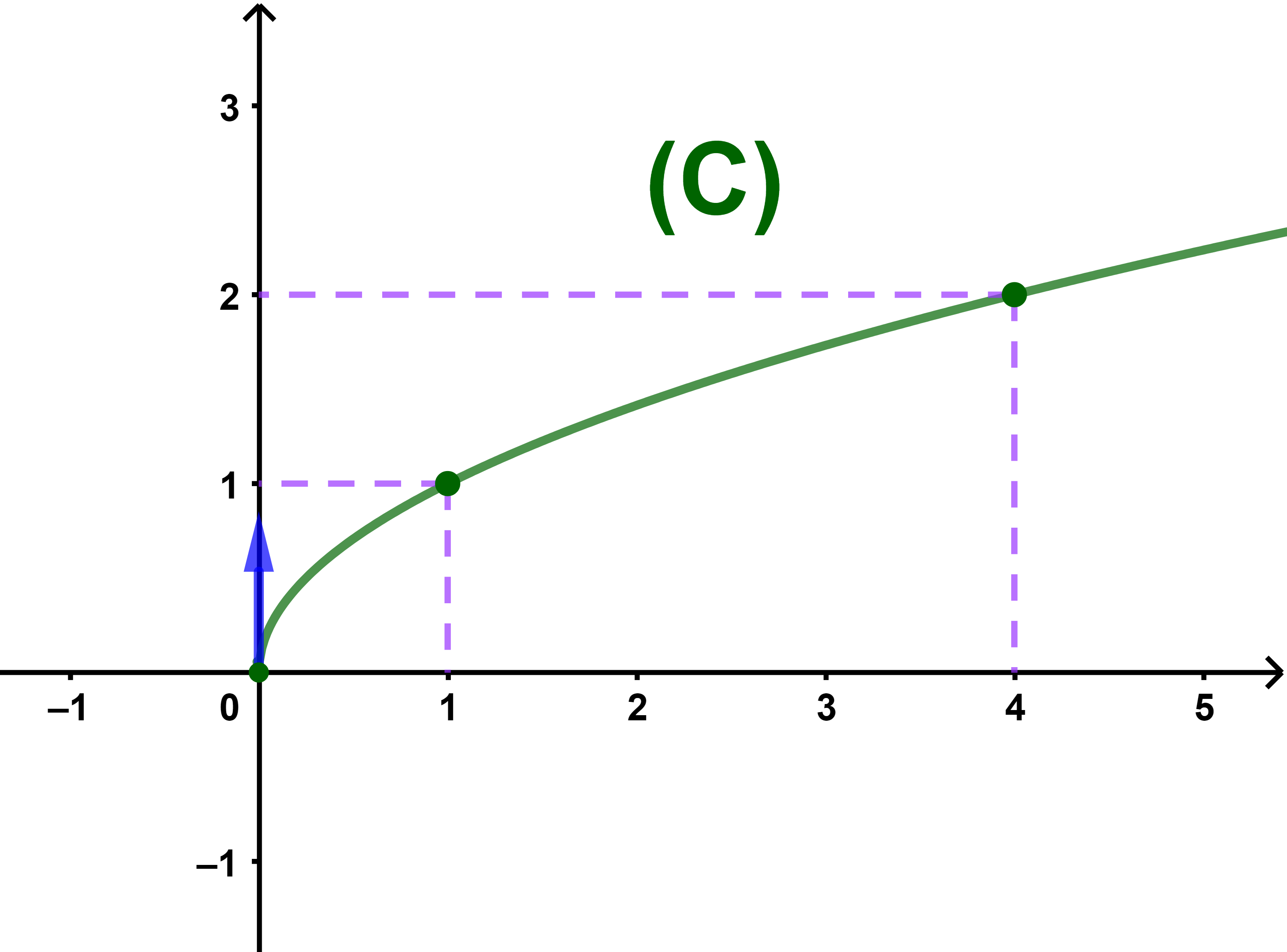
2.2.2 La fonction x→√(ax+b)
Soit f la fonction définie par
f(x)=√(ax+b).
1) a>0
l'ensemble de définition de f
| D = [- | b | ; +∞[ | |
| a |
f est dérivable sur
| I = ]- | b | ; +∞[ | |
| a |
| f'(x) = | (ax + b)' | = | a |
| 2√(ax + b) | 2√(ax + b) |
2) a < 0
| D = ]-∞ ; | b | ] | |
| a |
| f est dérivable sur J = ]-∞ ; | -b | [ |
| a |
| f '(x) = | a |
| 2√(ax + b) |
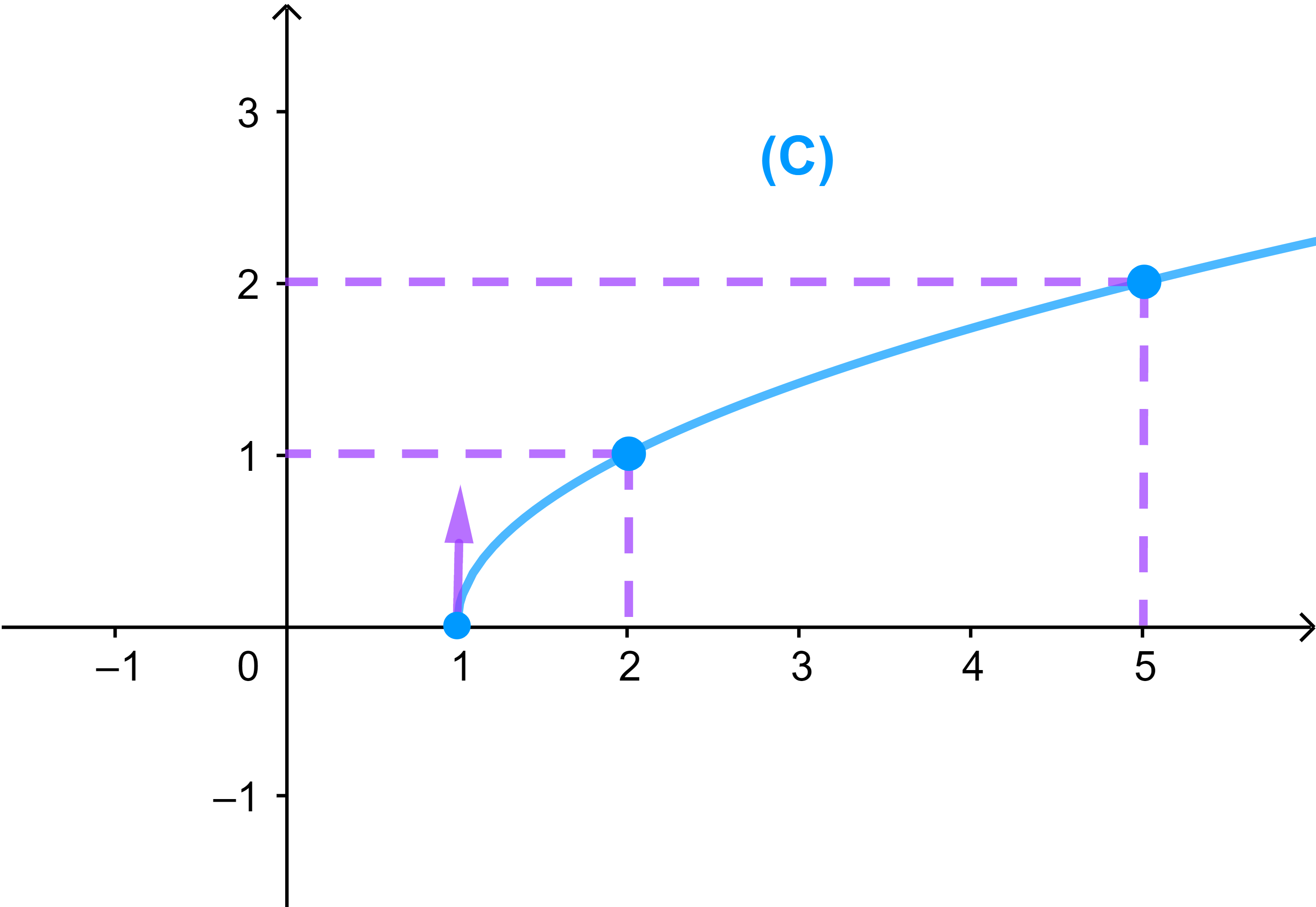
Exemple 1
Soit f une fonction définie par
f(x)=√(x-1)
et (C) sa courbe représentative dans un repère orthonormé.
1) f est définie si x-1≥0
donc D=[1;+∞[.
2) Limite de f en +∞
lim +∞ |
x - 1 = | lim +∞ |
x = +∞ |
| Donc | lim +∞ |
f(x) | = +∞ |
3) f est dérivable si x-1>0 ou encore si x>1
donc f est dérivable sur I=]1;+∞[.
Soit x∈I
| f'(x) = | (x - 1)' | = | 1 |
| 2√(x - 1) | 2√(x - 1) |
Pour tout x∈I on a f'(x)>0 car 1>0
donc f est strictement croissante sur I
4) Tableau de variation de f
| x | 1 | +∞ | |
| f'(x) | || | + | |
| 0 | ↗ | +∞ |
5) La courbe représentative de f