ُExercice 1 tp

Soit f une fonction numérique définie par

f(x) =	x + 1
	x + 2

et C) sa courbe dans un repère orthonormé
(O;i^→;j^→)
1) Déterminer D ensemble de définition de f

2) Calculer les limites suivantes

lim - ∞	f(x)		lim + ∞	f(x)
lim (-2)-	f(x)		lim (-2)+	f(x)

et déduire les asymptotes de (C)
3) (a) Calculer f'(x) tel que x∈D et étudier la monotonie de f
(b) Tracer le tableau de variations de f 4) Tracer les deux asymptotes et la courbe (C)

Correction

1) f est définie si x+2≠0 ou encore si x≠-2
donc D=IR\{-2}=]-∞;-2[∪]-2;+∞[
2) Limites et adymptotes

lim -∞	f(x) =	lim -∞	x	= 1
			x

et cela signifie que (C) admet une asymptote d'équation y=1 au voisinage de -∞

lim +∞	f(x) =	lim +∞	1x	= 1
			x

Et cela signifie que (C) admet une asymptote d'équation y=2 au voisinage de +∞

2) On étudie d'abord le signe de x+2 au voisinage de -2
On pose p(x)=2x-1 et q(x)=x-1
p(-2)=(-2)+1=-1

x		-∞		-2		+∞
x + 2			-	||	+

Si x → (-2)^- alors q(x) → 0^-

lim (-2)-	f(x)	=	-1	= + ∞
			0-

Ainsi (D): x = -2 est une asymptote à (C) à gauche à -2
Si x → (-2)⁺ alors q(x) → 0⁺

lim (-2)+	f(x)	=	-1	= - ∞
			0+

ainsi (D): x=-2 est une asymptote à (C)à droite à -2

4) f est une fonction rationnelle donc dérivable sur D . Soit x∈D

f '(x) =	1(x+2) - (x+1)(1)
	(x+2)²
=	x + 2 - x - 1
	(x+2)²

ainsi pour tout x∈D on a

f ' (x) =	1
	(x + 2)²

Signe de f'(x)
On a 1 > 0 et (x+2)²>0
donc (∀x∈IR \{1}) on a f'(x)>0
et cela signifie que f est strictement croissante sur ]-∞;-2[ et strictement croissante aussi sur ]-2 ; +∞[
Tableau de variations de f

x		-∞			-2			+∞
f '(x)			+		||		+
f		1	↗	+∞	||	-∞	↗	1

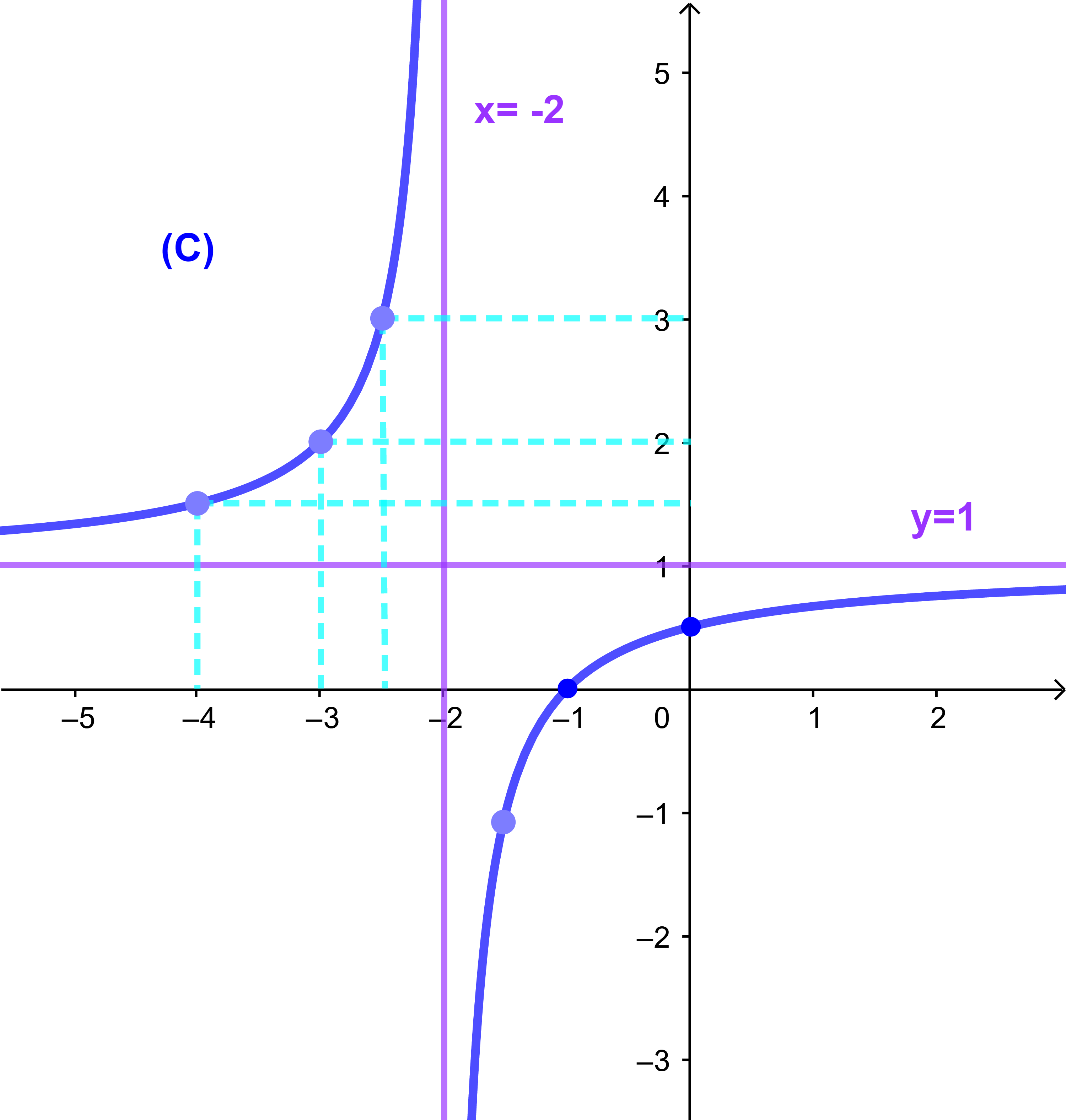
5) La courbe (C)