Rappel
Soient f une fonction numérique de la variable réel x et (C) sa courbe représentative dans un repère orthonormé
(O;i^→;j^→)
1) Si l'une des coordonnées d'un point M(x;y) de la courbe (C) tend vers ∞ alors la courbe admet une branche infinie
(c'est à dire x→±∞ ou f(x)→±∞).

Cas (x→-∞ et f(x)→+∞)

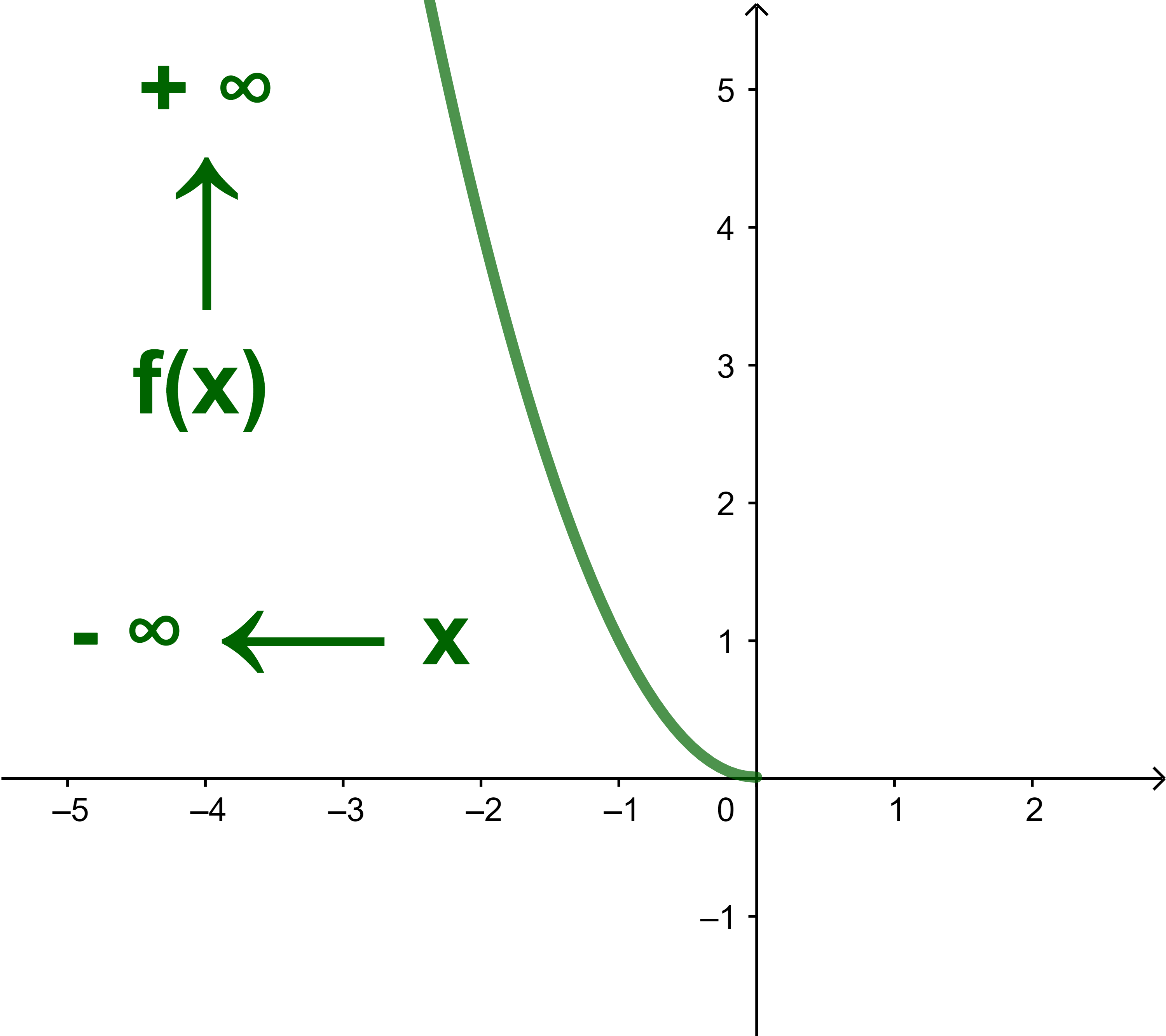
Cas (y→ - ∞ avec y=f(x))

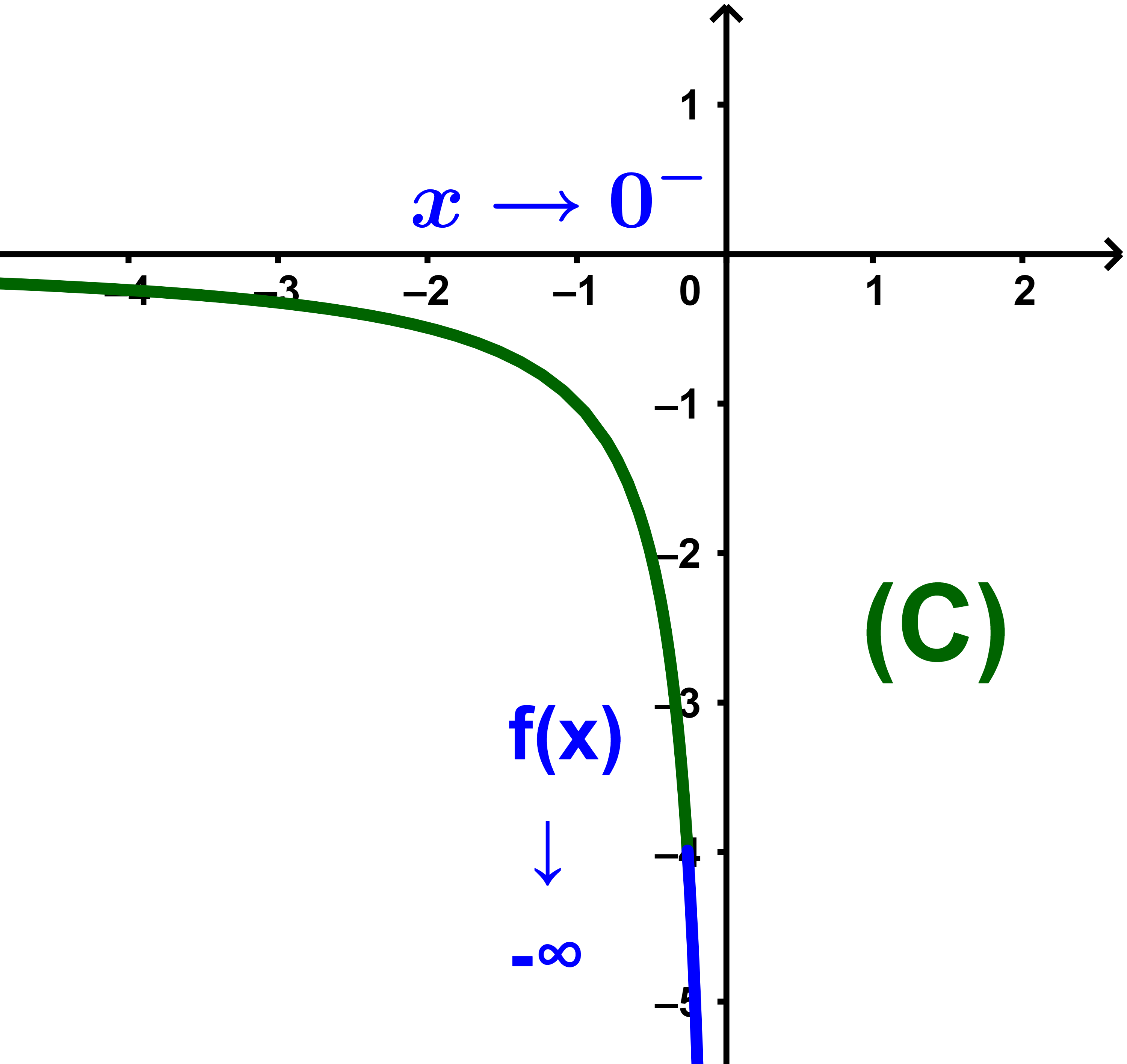
2) La droite d'équation x=a est asymptote à (C) Si l'une des conditions suivantes est vérifiée

lim a-	f(x) = +∞		lim a-	f(x) = -∞
lim a+	f(x) = +∞		lim a+	f(x) = -∞

3) La droite d'équation y=b est asymptote à (C) au voisinage de -∞ ou +∞

Si

lim -∞

f(x) = b

ou

Si

lim + ∞

f(x) = b

Exercice 1 tp

Soit f une fonction numérique définie par

f(x) =	-2x - 1
	x + 1

Déterminer les asymptotes de la courbe de f.

Correction

f est définie si x+1≠0 ou encore si x≠-1
donc D=]-∞;-1[∪]-1;+∞[.

On a D=]-∞;-1[∪]-1;+∞[.
Il y a donc quatre bornes

- ∞

(-1)-

(-1)+

+ ∞

1) On étudie les deux cas (-1)^- et (-1)⁺.
On pose p(x)=-2x-1 et q(x)=x+1.
p(-1)=-2(-1)-1=1 et q(-1)=-1+1=0.

On étudie d'abord le signe de x+1.

x		-∞		-1		+∞
x + 1			-	0	+

(i) Si x → (-1)^- alors q(x) → 0^-

lim (-1)-	f(x)	=	1	= - ∞
			0-

ainsi la droite (D): x=-1 est asymptote à (C) à gauche à -1.
(ii) Si x → (-1)⁺ alors q(x) → 0⁺

lim (-1)+	f(x)	=	1	= + ∞
			0-

donc la droite (D): x=-1 est asymptote à (C) à droite à -1.

2) On étudie les deux cas -∞ et +∞.

lim -∞	f(x) =	lim -∞	-2x	= -2
			x

donc la droite (D): y=-2 est asymptote à (C) au voisinage de -∞.

lim +∞	f(x) =	lim +∞	-2x	= -2
			x

donc la droite (D): y=-2 est asymptote à (C) au voisinage de +∞.