Dérivation (1)
Exercice 1 tp
Soit f une fonction numérique définie par
f(x)=x³+x².
Montrer que f est dérivable en 1
puis déterminer l'équation de la tangente à la courbe de f au point A(1;f(1)).
Correction
D=IR donc 1∈D et pour montrer que f est dérivable en 1 il suffit de montrer que
lim x→1 |
f(x)-f(1) | ∈IR | (un nombre fini) |
| x-1 |
lim x→1 |
f(x)-f(1) | = | lim x→1 |
x³+x²-2 |
| x-1 | x-1 |
p(x)=x³+x²-2 est un polynôme et s'annule en 1 car p(1)=0
donc il est divisible par x-1.
On effectue donc la division euclidienne de p(x) par x-1.
| x³ | +x² | +0x | -2 | x-1 | ||
| -x³ | +x² | x²+2x+2 | ||||
| 0 | +2x² | +0x | -2 | |||
| -2x² | +2x | |||||
| 0 | 2x | -2 | ||||
| -2x | +2 | |||||
| 0 | 0 |
et donc p(x)=(x-1)(x²+2x+2).
lim x→1 |
f(x)-f(1) | = | lim x→1 |
(x-1)(x²+2x+2) |
| x-1 | x-1 |
| = | lim x→1 |
(x²+2x+2) = 5 |
et cela signifie que f est dérivable en 1 et f'(1)=5
ainsi (C) admet une tangente au point A(1;2) d'équation
T: y=f'(1)(x-1)+f(1) ou encore T: y=5x-3.
Notons que f est un polynôme
donc dérivable sur IR et en particulier au point 1.
Exercice 2 tp
Soit f une fonction numérique définie par
f(x)=√(x).
1) Etudier la dérivabilité de f en 0.
2) Est ce que la courbe (C) admet une tangente au point O ?
Correction
1) D=[0;+∞[ donc 0∈D et f(0)=0.
lim x→0+ |
f(x)-f(0) | = | lim x→0+ |
√(x) - 0 |
| x-0 | x |
| = | lim x→0+ |
1 | = +∞ | ∉IR |
| √(x) |
donc f n'est pas dérivable en 0.
2) f n'est pas dérivable en 0 donc la courbe (C) n'a pas de tangente au point O, mais elle admet une demi-tangente verticale vers le haut.
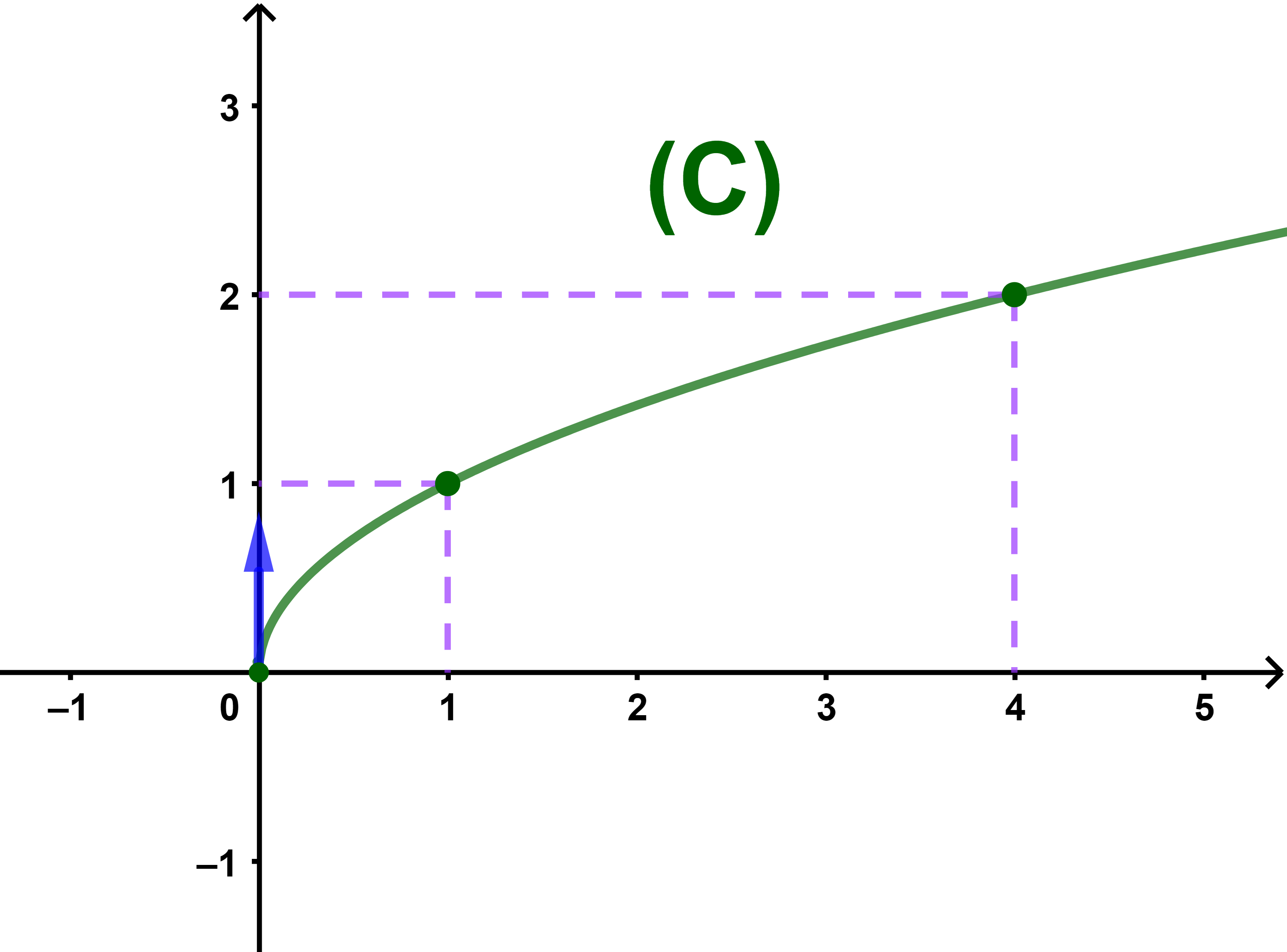
Propriété Soit a∈D.
Si une fonction f n'est pas dérivable au point a
| et | lim x→a |
f(x)-f(a) | = ±∞ |
| x-a |
alors la courbe (C) admet une demi-tangente au point d'abscisse a.