1- المجموعة وجزء مجموعة

1.1 المجموعة

1.1.1 تعريف

المجموعة هي كائن يجمع عناصر اذا كانت موجودة
ونرمز لمجموعة باحد الحروف التالية, E; F; G; ..

1.1.2 ترميز

1) المجموعة التي لا تحتوي على اي عنصر تسمى المجموعة الفارغة ونرمز لها ب ∅
2) اذا كان x عنصرا من مجموعة E, نكتب x∈E ونقرأ x ينتمي الى E
والا نكتب x∉E ونقرأ x لا ينتمي الى E

1.1.3 امثلة

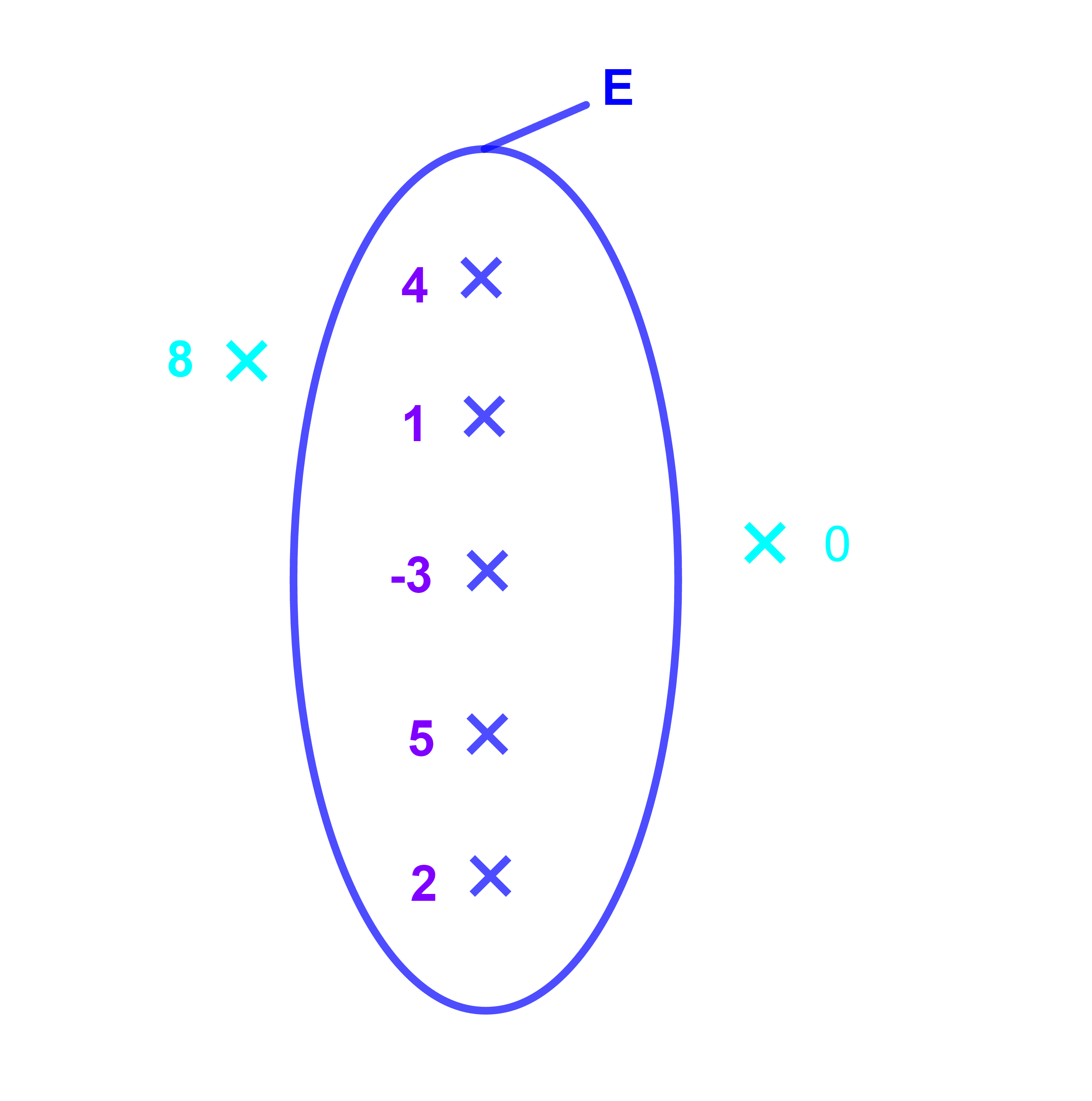
نعتبر المجموعة E={-3;1;2;4;5}
لدينا 2 عنصرا من E اذن 2∈E
5 عنصر من E اذن 5∈E
0 ليس عنصرا من E اذن 0∉E

1.2 المجموعة بتفصيل

1.2.1 تعريف

المجموعة بتفصيل هي قائمة من العناصر

1.2.2 مثال

E={-3;1;2;4;5}

1.3 المجموعة بادراك

1.3.1 تعريف

المجموعة ب بادراك هي مجموعة معرفة بخاصية

1.3.2 امثلة

1) E={x∈IN/ 0< x < 10 ; زوجي x و}
2) F={x∈ℤ/ |x|< 7}

ملاحظة

توجد حالات يمكن كتابة مجموعة بادراك بتفصيل

تمرين 1

اكتب المجموعات التالية بتفصيل
A=IN∩[-2;√(30)]
B={x∈ℤ/ x|20}
C={x∈IN/x+4|x+19}

تمرين 2

اكتب المجموعات التالية بادراك
E={1;3;5;7;9;11;13;15}
F={0;7;14;21;28;25;42;49}
G={1;2;4;5;8;10}

1.4 جزء من مجموعة

1.4.1 امثلة

نعتبر المجموعة ℤ التي تتكون من جميع الاعداد الصحيحة الموجبة ومقابلاتها, تتضمن المجموعة IN
IN هي جزء من ℤ ونكتب IN⊂ℤ ونقرأ IN ضمن ℤ
ℤ⊂ℚ
ℚ⊂ℝ

1.4.2 تعريف

لتكن E و F مجموعتين غير فارغتين F ضمن E ونكتب F⊂E, اذا كان كل عنصر من عناصر F هو عنصر من عناصر E
بعبارة اخري
F⊂E ⇔ (∀x∈ F): x∈E.

1.5 مجموعة اجزاء مجموعة

1.5.1 مثال:

نعتبر المجموعة E={1;2}
حدد جميع الاجزاء الممكنة للمجموعة E

تصحيح

1) المجموعة التي لا تحتوي على اي عنصر, ∅, المجموعة الفارغة هي جزء لكل مجموعة غير فارغة E
2) المجموعة المكونة من عنصر واحد تسمى الاحادية, يوجد جزءان من E, الاحادية {1} والاحادية {2}
3) المجموعة المكونة من عنصرين يوجد جزء واحد من E
وبالتالي يوجد اربعة اجزاء من E التي تحدد مجموعة اجزاء E, ونرمز لها ب P(E)={∅;{1};{2};E}

1.5.3 تعريف

E مجموعة غير فارغة, الاجزاء الممكنة للمجموعة E تكون مجموعة اجزاء E, ونرمز لها ب ℙ(E)

1.5.4 خاصيات

لتكن E مجموعة منتهية
∅⊂P(E) و E⊂P(E)
F⊂ℙ(E) ⇔ F⊂E

تمرين:

لتكن E={e;f;g} حدد ℙ(E)

2- التضمن والتساوي والمتممة

2.1 التضمن

2.1.1 انشطة

نعتبر المجموعات E={1;2;5;7;8;10;13} ; F={2;5;7} ; G={0;4;8;13}

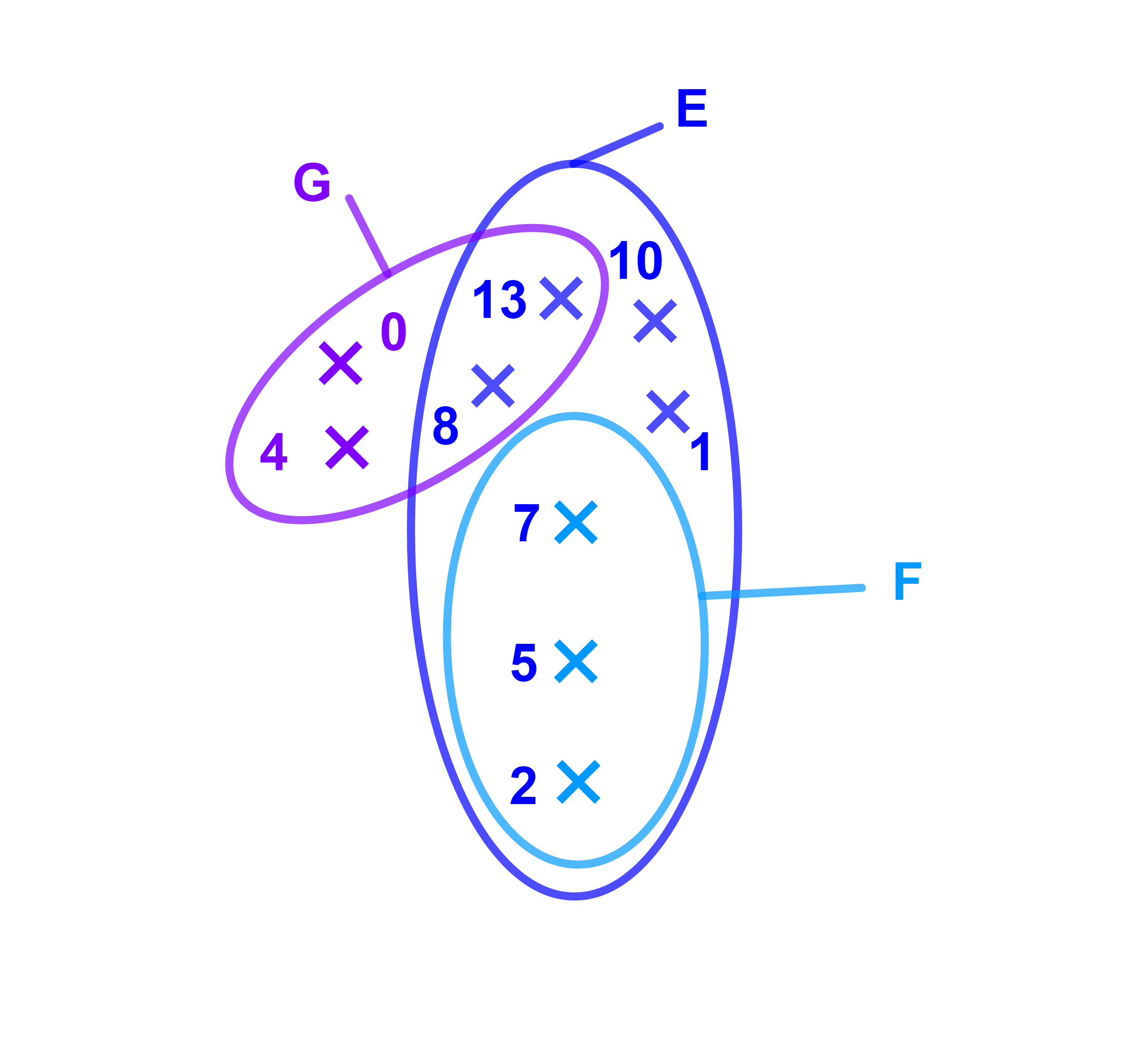
لدينا عناصر F هي 2;5; 7 وكلها من عناصر E
اذن F هي جزء من E, ونكتب F⊂E ونقرأ F ضمن E
0 هو عنصر من G ولكن 0∉E اذن G ليست ضمن E, ونكتب G⊄E

2.1.2 تعريف

لتكن E و F مجموعتين
نقول ان F ضمن E ونكتب F⊂E اذا كان كل عنصر من عناصر F ينتمي الى E
بعبارة اخرى
F⊂E ⇔ (∀x): x∈F ⇒ x∈E

2.2 التساوي

2.2.1 انشطة

نعتبر المجموعات E={x∈ℤ/ -2< x< 3} ; F={-1;0;1;2} ; G={-1;2}
لدينا -1∈G و -1∈F
وايضا 2∈G و 2∈F اذن كل عنصر من G يوجد في F ومنه فان G⊂F

لاحظ ايضا كل عناصر F هي اعداد صحيحة محصورة بين -2 و 3 اذن F⊂E
وايضا اذا كان x∈E فان -2< x< 3 وبما ان x عدد صحيح فان x=-1 او x=0 او x=1 او x=2 , جميع هذه العناصر هي عناصر F ومنه فان E و F مجموعتان مكونتان من نفس العناصر وبالتالي E=F

2.2.2 تعريف

E و F متساويتان ونكتب E=F اذا كانتا مكونتين من نفس العناصر
بعبارة اخرى
E=F ⇔ F ⊂ E و E ⊂ F

2.2.3 خاصيات

E ; F و G ثلاث مجموعات
(G⊂F و F⊂E) ⇒ G⊂E
E=F⇔(∀x): x∈E ⇔ x∈F.