2.3 المتممة

2.3.1 تعريف

A جزء من E
مجموعة عناصر E التي لاتنتمي الى A تسمى متممة A في E ونكتب C^A_E او Ā
Ā={x ∈E / x ∉A}

2.3.2 خاصية

متممة Ā في E هي الجزء A

2.3.3 مثال

متممة الاعداد الطبيعية الزوجية في المجموعة IN هي مجموعى الاعداد الفردية
متممة الاعداد اللاجذرية في IR هي مجموعة الاعداد الجذرية

تمرين

نعتبر المجموعة E={0;5;10;15;20;25;30;35;40;45}
لتكن U={x∈E / x=2k, k∈IN}
1) اكتب F بتفصيل
2) حدد Ū

3- التقاطع والاتحاد والجذاء الديكارتي

3.1 تقاطع مجموعتين

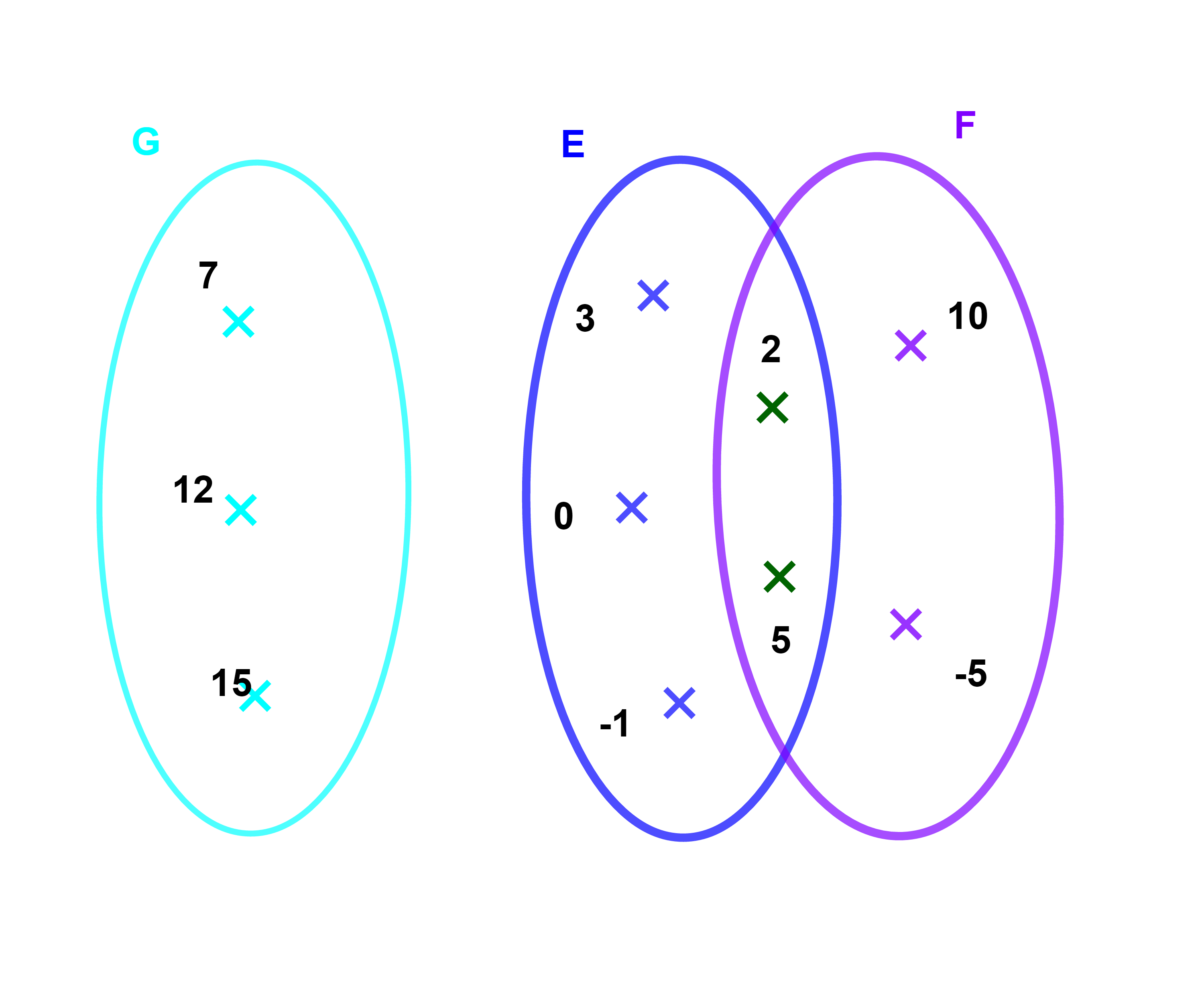
3.1.1 مثال

E={-1;0;2;3;5};
F={-5;2;5;10}
G={7;12;15}, العناصر المشتركة بين E و F هي 2 و 5
المجموعة {2;5} هي تقاطع E و F
ونكتب E∩F={2;5}
اذا لم يوجد اي عنصر بين E و G نقول ان E و G منفصلتان E∩G=∅

3.1.2 تعريف

E و F مجموعتان, تقاطع E و F ونكتب E∩F هو مجموعة العناصر المشتركة بينهما
E∩F={x / x∈E∧x∈F}

3.1.3 خاصيات

1) E∩F =F ⇔ F⊂E
2) (E∩F)⊂E و (E∩F)⊂F
3) G⊂(E∩F)⇒(G⊂E و G⊂F)

3.2 اتحاد مجموعتين

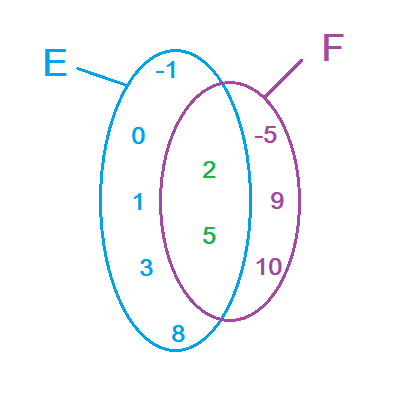
3.2.1 مثال

E={-1;0;1;2;3;5;8}; F={-5;2;5;9;10}
المجموعة المكونة من كل عناصر E وعناصر F هي:
{-5;-1;0;1;2;3;5;8;9;10} وتسمى اتحاد المجموعتين E و F ونكتب E∪F

3.2.2 تعريف

E و F مجموعتان, اتحاد E و F ونكتب E∪F هو المجموعة المكونة من كل عناصر E ومن عناصر F
E∪F={x / x∈E∨x∈F}

3.2.3 خاصيات

1) E∪F=E⇔F⊂E
2) E⊂(E∪F) و F⊂(E∪F)
3) G⊂(E∪F)⇏G⊂E او G⊂F. مثال:
E={2;4;5}; F={1;3} و G={1;4;5}, G⊂E∪F لكن G⊄E و G⊄F.

3.3 فرق مجموعتين

3.3.1 تعريف

E و F مجموعتان
E\F={x∈E/ x∉F}.
EΔF=(E\F)∪(F\E)

3.3.2 مثال

لتكن E={-1 ; 0 ; 1 ; 2 ; 3 ; 5}
F={-4 ; 2 ; 5 ; 9} لدينا
E\F={-1 ; 0 ; 1 ; 3} و F\E={-4 ; 9}.
EΔF={-4 ; -1 ; 0 ; 1 ; 3 ; 9}

3.3.3 ملاحظة

EΔF=(E∪F)\(E∩F)

3.4 قانون مورغان

3.4.1 خاصية

E ; F و K مجموعات
E ∩ (F ∪ G) = (E ∩ F) ∪(E ∩ G)
E ∪ (F ∩ G) = (E ∪ F) ∩ (E ∪ G)

3.4.2 تطبيق

حل في IR×IR النظمة (x²-1=0 و y=2)

تصحيح

(x²-1=0 و y=2)⇔(x-1)(x+1) و y=2
⇔ (x=1 او x=-1) و y=2
للتذكير (او≡∪) ; (و ≡ ∩)
وبتطبيق قانون مورغان
(x²-1=0 و y=2)⇔(x=1 و y=2) او (x=-1 و y=2)
وبالتالي S={(1;2) ; (-1;2)}

3.4.3 خاصيات

E ; F و K اجزاء من H
Ē∩E=∅ ; Ē∪E=H
E∩(F∩G) = (E∩F)∩G
E∪(F∪G) = (E∪F)∪G

3.5 الجذاء الديكارتي

3.5.1 مثال

E×F	1	2	3
a	(a;1)	(a;2)	(a;3)
b	(b;1)	(b;2)	(b;3)
نتيجة:	cardE×F=6=cardE×cardF

3.5.2 تعريف

الجذاء الديكارتي للمجموعتين E و F ونكتب E×F هو مجموعة ازواج (x;y) بحيث x∈E و y∈F.
بعبارة اخرى
E×F={(x;y)/ x∈E و y∈F}
الترتيب مهم !