1.5 Ensemble des parties d’un ensemble

1.5.1 Exemple

Soit E={1;2}
Déterminer toutes les parties possibles de E.

Correction
1) Ensembe qui ne contient aucun élément est l'ensemble vide ∅.
Notons que l'ensemble vide est une partie de tout ensemble donc c'est une partie de E.

2) Ensemble constitué d'un seul élément est nommé singleton.
Il y a deux singletons {1} et {2} qui sont inclus dans E.
3) Ensemble constitué de deux éléments est l'ensemble E.
L'ensemble des parties de E est noté ℙ(E).
ℙ(E)={∅;{1};{2};E}.

1.5.2 Définition

Soit E un ensemble fini.
Les parties possibles de E constituent l'ensemble des parties de E et est noté ℙ(E).

1.5.3 Propriétés

Soit E un ensemble fini
1) ∅⊂ℙ(E) et E⊂ℙ(E).
2) (F⊂ℙ(E)) ⇔ (F⊂E).

Exercice 1 tp

Soit E={e;f;g} un ensemble.
Déterminer ℙ(E).

2- Inclusion - égalité - complémentaire

2.1 Inclusion

2.1.1 Activité

Soient E={1;2;5;7;8;10;13} et F={2;5;7} deux ensembles finis.
Les éléments de F sont tous des éléments de E. F est donc une partie de E.
On écrit F⊂E et on lit F est inclu dans E.

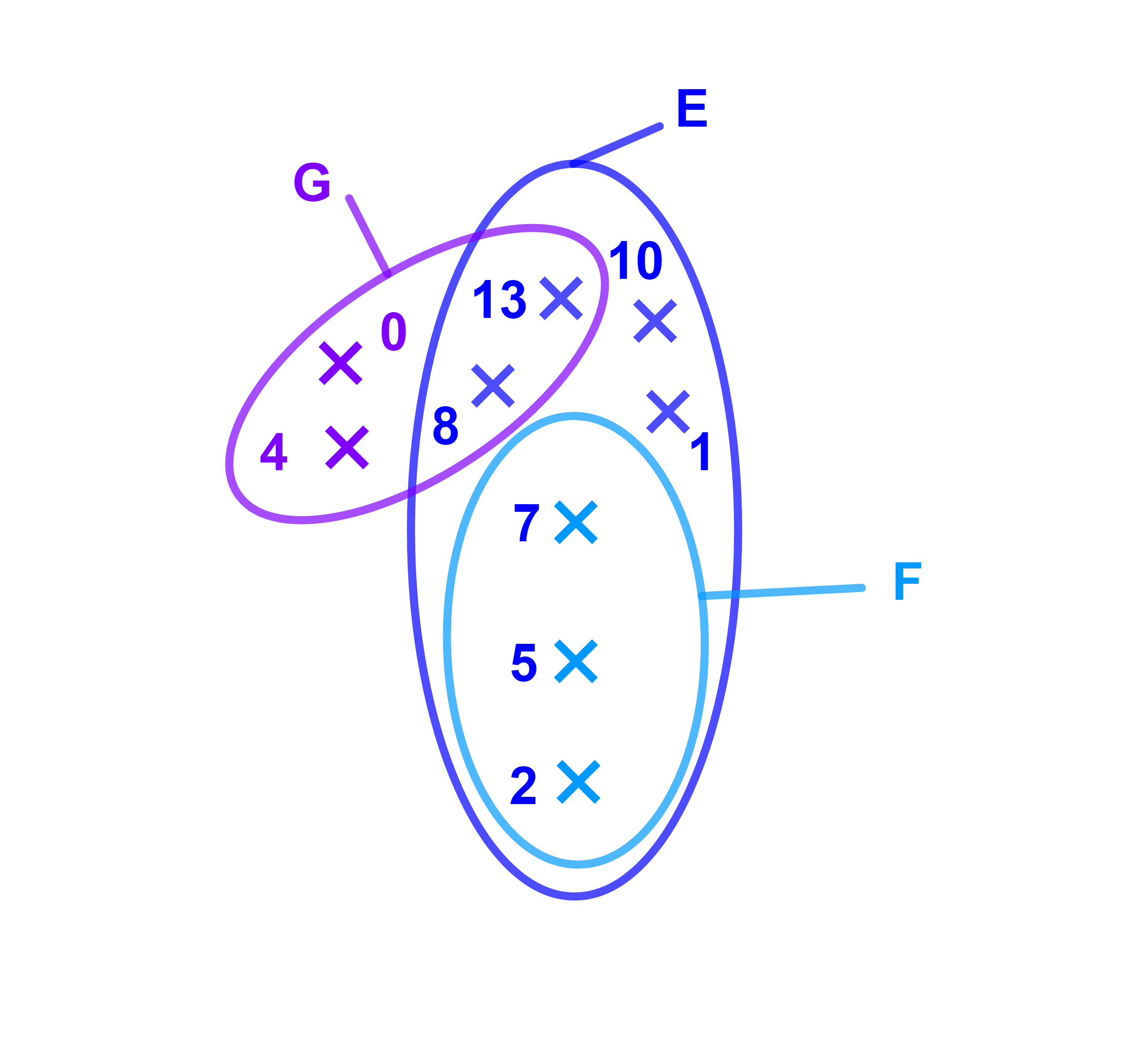
Soit G={0;4;8;13} un ensemble fini.
0 est un élément de G mais 0∉E
donc G n'est pas une partie de E.
On écrit G⊄E et on lit G n'est pas inclu dans E.

2.1.2 Définition

Soient E et F deux ensembles
On dit F est inclu dans E et on écrit F⊂E si tout élément de F appartient à E.
En d'autre terme
F⊂E ⇔ x∈F ⇒ x∈E.

2.2 Egalité

2.2.1 Activité

Soient E={x∈ℤ/ -2<x<3} et F={-1;0;1;2} deux ensembles.
1) Les éléments de F sont des entiers strictement compris entre -2 et 3 donc F⊂E.
2) x∈E ⇔ -2<x<3 et x∈ℤ
⇔ x=-1 ou x=0 ou x=1 ou x=2
⇔ E={-1;0;1;2}.
Les éléments de E sont égalements des éléments de F donc E⊂F.

E et F sont donc égaux et on écrit E=F.

2.2.2 Définition

Soient E et F deux ensembles.
On dit que E et F sont égaux s'ils sont constitués par les mêmes éléments et on écrit E=F.
En d'autre terme
E=F ⇔ F⊂E et E⊂F.

2.2.3 Propriétés

Soient E ; F et G trois ensembles.
1) (G⊂F et F⊂E) ⇒ G⊂E.
2) E=F ⇔ (∀x∈E): x∈F et (∀x∈F): x∈E.