2.3 Le complémentaire

2.3.1 Définition

Soit A une partie d'un ensemble E
L'ensemble des éléments de E qui n'appartiennent pas à A est appelé complémentaire de A dans E.

En d'autre terme
Ā={x∈E / x∉A} est le complémentaire de A dans E.

Exercice 1 tp

Soient E={0;5;10;15;20;25;30;35;40;45}
et U={x∈E / x=2k avec k∈IN} deux ensembles.
1) Ecrire F en extension.
2) Déterminer Ū.

2.3.2 Propriété

Soit A une partie d'un ensemble E et Ā son complémentaire dans E.
Le complémentaire de Ā dans E est la partie A.
En d'autre terme Ā = A.

3- Intersection - Réunion - Produit cartésien

3.1 Intersection de deux ensembles

3.1.1 Exemple

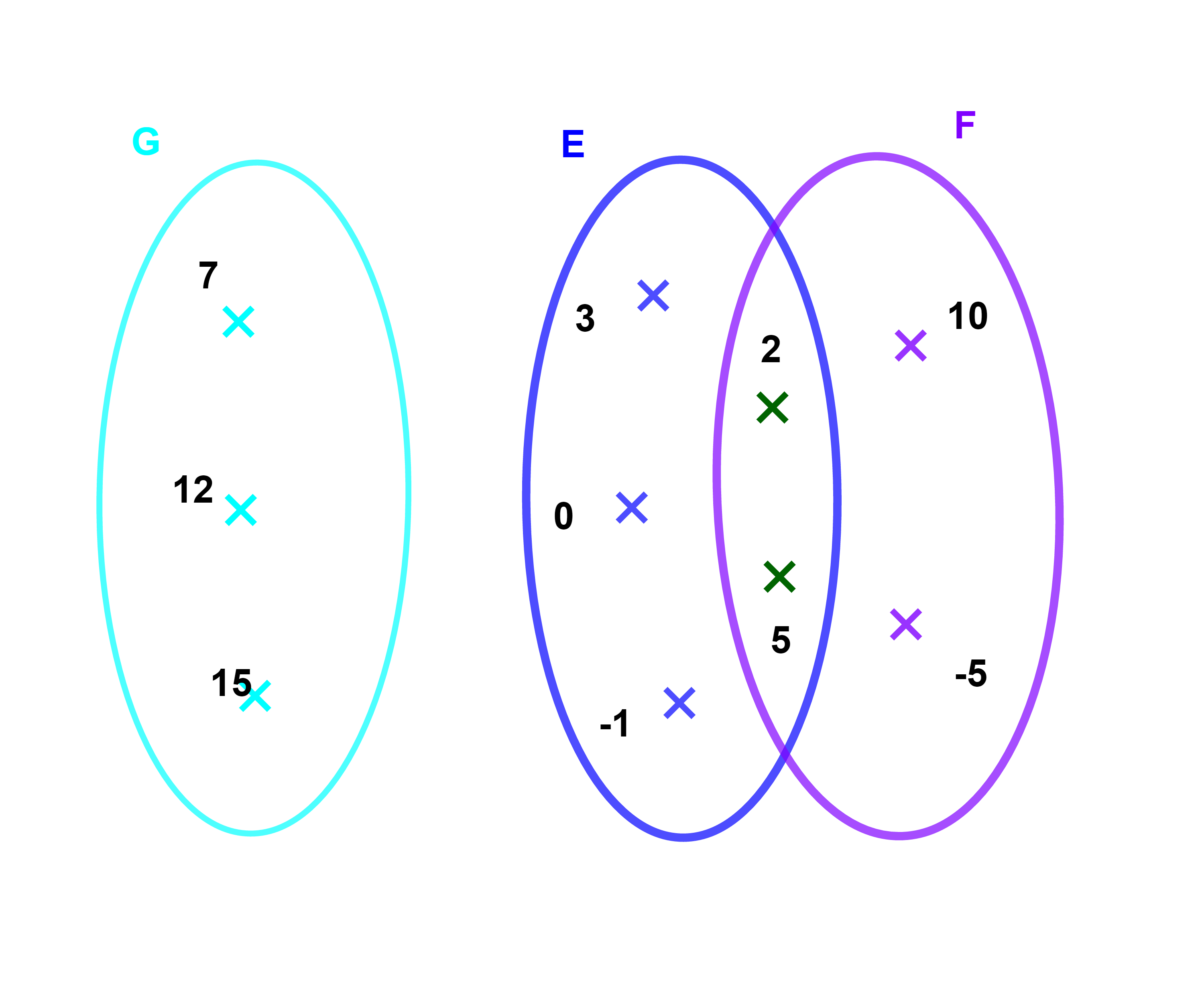
Soient E={-1;0;2;3;5} et F={-5;2;0;10} deux ensembles.
1) Les éléments communs entre E et F constituent l'ensemble {2;5} appelé intérsection de E et F et on écrit E∩F.

2) On considère l'ensemble G={7;12;15}.
il n y'a aucun élément commun entre E et G.
On dit que E et G sont disjoints
et on écrit E∩G=∅.

3.1.2 Définition

Soient E et F deux parties d'un ensemble K.
L'intersection de E et F est l'ensemble des éléments qu'ils ont en commun et on écrit E∩F.
En d'autre terme E∩F={x∈K / x∈E et x∈F}.

3.1.3 Propriétés

Soient E ; F et G trois parties d'un ensemble K.
1) E∩F=F ⇔ F⊂E.
2) (E∩F)⊂E et (E∩F)⊂F.
3) G⊂(E∩F)⇒(G⊂E et G⊂F).

3.2 Réunion de deux ensembles

3.2.1 Exemple

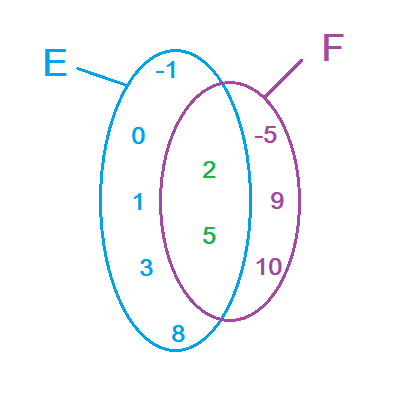
Soient E={-1;0;1;2;3;5;8} et F={-5;2;5;9;10} deux ensembles.
{-5;-1;0;1;2;3;5;8;9} est l'ensemble constitué par tous les éléments de E et F.
On écrit E∪F et on lit E union F.

3.2.2 Définition

Soient E et F deux parties d'un ensemble K.
l'union de E et F est l'ensemble de tous les éléments de E et F et on écrit E∪F.

En d'autre terme E∪F={x∈K / x∈E ou x∈F}.

3.2.3 Propriétés

Soient E ; F et G trois ensembles.
1) E∪F=E ⇔ F⊂E.
2) E⊂(E∪F) et F⊂(E∪F).
3) G⊂(E∪F) ⇏ G⊂E ou G⊂F.
Contre exemple
On considère E={2;4;5} ; F={1;3} et G={1;4;5}.
G⊂E∪F mais G⊄E et G⊄F.