تمرين 1 tp

اكتب المجموعات التالية بتفصيل
A=IN∩[-2;√(30)]
B={x∈ℤ/ x|20}
C={x∈IN/ x+4|x+19}

تمرين 2 tp

اكتب المجموعات التالية بادراك
E={1;3;5;7;9;11;13;15}
F={0;7;14;21;28;25;42;49}
G={1;2;4;5;8;10}

تمرين 3 tp

نعتبر المجموعة
E={0;5;10;15;20;25;30;35;40;45}
لتكن U={x∈E / x=2k, k∈IN}
1) اكتب F بتفصيل
2) حدد Ū

تمرين 4 tp

حل في IR×IR النظمة (x²-1=0 و y=2)

تصحيح

(x²-1=0 و y=2)⇔(x-1)(x+1) و y=2
⇔ (x=1 او x=-1) و y=2
للتذكير (او≡∪) ; (و ≡ ∩)
وبتطبيق قانون مورغان
(x²-1=0 و y=2)⇔(x=1 و y=2) او (x=-1 و y=2)
وبالتالي S={(1;2) ; (-1;2)}

تمرين 5 tp

حل النظمة التالية

{	x(y-1)+y-1=0
	x²+x=y+xy

تمرين 6 tp

حل مبيانيا النظمة التالية

{	(x-y)(x+y-2) >0
	-2 < x < 3

تصحيح

{	(x-y)(x+y-2) >0
	-2 < x < 3

⇔

	((x-y> 0) ∧ (x+y-2>0)) ∨ (((x-y< 0) ∧ (x+y-2< 0))
	-2 < x < 3

⇔

∨	((x-y> 0) ∧ (x+y-2>0)) ∧ -2 < x < 3
	(((x-y< 0) ∧ (x+y-2< 0)) ∧ -2 < x < 3

نعتبر المستقيمين (D1): x-y=0 ; (D2): x+y-2=0 وننشئهما في نفس المعلم
ثم ندرس اشارة كل من العددين x-y ; x+y-2 (تجويه المستوى)

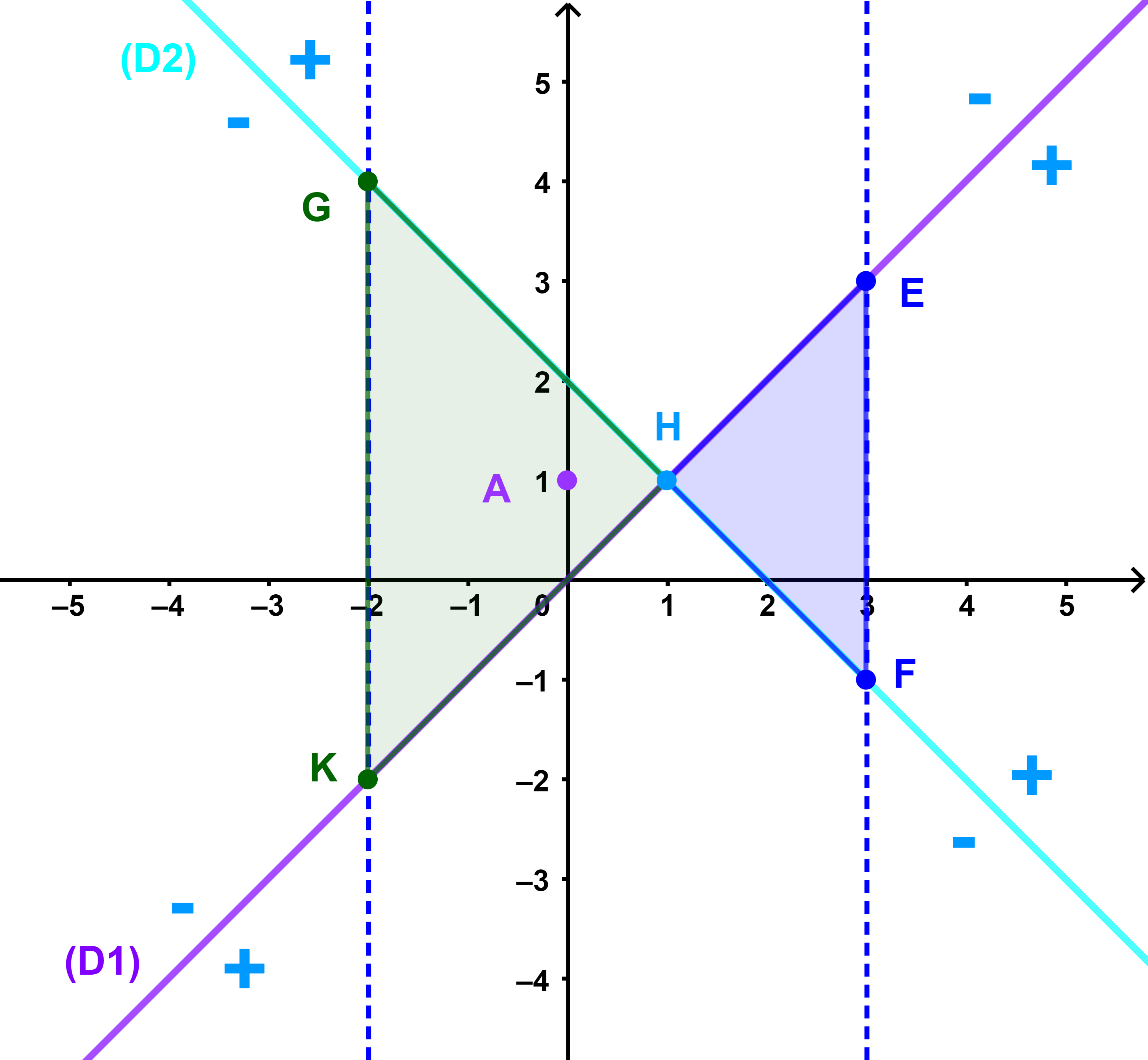
1) اشارة x-y
نعتبر نقطة من المستوى لا تنتمي الى (D1) فلتكن A(0;1)
لدينا 0-1=-1< 0 اذن نصف المستوى الذي حدوده (D1) ويحتوى على النقطة A معرف بالمتراجحة x-y < 0
2) اشارة x+y-2
نعتبر نقطة من المستوى لا تنتمي الى (D1) فلتكن O(0;0)
لدينا 0+0-2=-2< 0 اذن نصف المستوى الذي حدوده (D2) ويحتوى على النقطة O معرف بالمتراجحة
x+y-2 < 0
(1) ومنه فان حلول النظمة

∨	((x-y> 0) ∧ (x+y-2>0))
	-2 < x < 3

هو مجموعة ازواج احداثيات نقط الجزء المفتوح المحدد بالمثلث EFH

(2) وحلول النظمة

∨	((x-y< 0) ∧ (x+y-2< 0))
	-2 < x < 3

هو مجموعة ازواج احداثيات نقط الجزء المفتوح المحدد بالمثلث GHK
وبالتالي حلول النظمة

∨	((x-y> 0) ∧ (x+y-2>0)) ∧ -2 < x < 3
	(((x-y< 0) ∧ (x+y-2< 0)) ∧ -2 < x < 3

هو مجموعة ازواج احداثيات نقط الجزأين المفتوحين المحددين بالمثلثين EFH و GHK

تمرين 7 tp

لتكن f تطبيقا معرفا من ℚ² نحو IR بما يلي f(x;y)=x+y√2
1) بين ان f تبايني
2) هل التطبيق f شمولي ؟

تصحيح

1) ليكن (x;y) ; (z;t) من ℚ² بحيث f(x;y)=f(z;t)
نبين ان (x;y)=(z;t) لدينا
f(x;y)=f(z;t)⇒ x+y√2=z+t√2
⇒ x-z + (y-t)√2=0
⇒x-z=0 و y-t=0 لان x-z; y-t∈ℚ
⇒ x=z و y=t
⇒ (x;y)=(z;t)
ومنه فان f تبايني
2)التطبيق ليس شمولي
مثال مضاد √3∈IR ليس له سابق