تمرين 8 tp

ليكن f تطبيقا معرفا من [-1;+∞[ نحو IR+
بما يلي f(x)=x-2√(x)
1) بين ان التطبيق f ليس تباينيا
2) بين ان التطبيق f شمولي
3) نعتبر g قصور التطبيق f على [1;+∞[
بين ان التطبيق g تقابل

تصحيح

1) لدينا f(0)=f(4)=0 و 0≠4 اذن f ليس تباينيا
2) نبين ان f شمولي
ليكن y∈[-1;+∞[ , ∃x∈IR+ ?: f(x)=y
f(x)=y⇒ x-2√(x)=y
⇒ x-2√(x)-y=0
⇒ (√x)²-2.1.√(x)+1²-1-y=0 , x≥0
⇒ (√(x) -1)²=y+1
⇒ |√(x) -1|=√(y+1) , y≥-1
⇒ √(x)=1+√(y+1) او √(x)=1-√(y+1)

وبما ان 1+√(y+1)> 0 فان x يمكن ان يأخذ القيمة (1+√(y+1))² اي x= 2+y+2√(y+1)
3) نبين ان القصور g تقابل من [1;+∞[ نحو [-1;+∞[
ليكن y∈[-1;+∞[ , ∃!x∈[1; +∞[ ?: f(x)=y
f(x)=y⇒ x-2√(x)=y
حسب ما سبق لدينا
f(x)=y⇒ x-2√(x)=y
⇒ √(x)=1+√(y+1) او √(x)=1-√(y+1)
وبما ان x≥1 فان √x لا يمكن ان يأخذ القيمة 1-√(y+1) الا اذا كان y=-1
والا
√x=1+√(y+1)∈[1;+∞[
x=(1+√(y+1))²
ووحيد
اذن القصور g تقابل من [1;+∞[ نحو [-1;+∞[

تمرين 9 tp

ليكن f تطبيقا معرفا من المجموعة E نحو المجموعة F و A و B جزأين من E
1) (q1) بين ان f(A∩B)⊂f(A)∩f(B)
(q2) نفترض ان f تبايني
هل f(A∩B)=f(A)∩f(B) ?
2) بين ان f(A)∪f(B)=f(A∪B)

تصحيح

1) (q1) نبين ان f(A∩B)⊂f(A)∩f(B)
لدينا (A∩B) ⊂ A ⇒ f(A∩B) ⊂f(A)
و (A∩B) ⊂ B ⇒ f(A∩B) ⊂f(B)
اذن f(A∩B)⊂f(A)∩f(B)
(q2) حسب السؤال السابق f(A∩B)⊂f(A)∩f(B)
نبين اذن اذا كان f(A)∩f(B)⊂f(A∩B)
لدينا y∈f(A)∩f(B)⇒ y∈f(A) ∧ y∈f(B)
⇒ (∃x1∈A: f(x1)=y) ∧ (∃x2∈B: f(x2)=y)
وبما ان f تطبيق تبايني فان
y=f(x1)=f(x2)⇒ x1=x2=x

اذن ∃x∈A∩B / f(x)=y وهذا يعني ان y∈f(A∩B)
وبالتالي اذا كان f تبايني فان f(A∩B)=f(A)∩f(B)
2) نبين ان f(A)∪f(B)=f(A∪B)
للتذكير I=J ⇔((I⊂J) ∧ (J⊂I))
لدينا A⊂A∪B ⇒ f(A)⊂f(A∪B)
و B⊂A∪B ⇒ f(B)⊂f(A∪B)
اذن f(A)∪f(B)⊂f(A∪B)
نبين ان f(A∪B)⊂f(A)∪f(B)
لدينا y∈f(A∪B) ⇔ (∃x∈A∪B/ f(x)=y)
و x∈A∪B ⇔ x∈A ∨ x∈B
اذن ∃x∈A/ f(x)=y ∨ ∃x∈B/ f(x)=y
وهذا يعني ان y∈f(A) ∨ y∈f(B)
اي y∈f(A)∪f(B) اي f(A∪B)⊂f(A)∪f(B)
وبالتالي f(A∪B) = f(A)∪f(B)

تمرين 10 tp

A: B ; E اجزاء من المجموعة L
1) بين ان B∩Ā=B∩Ē ⇔B∩A=B∩E
2) تطبيق
L={x∈IN/ x|1120}
E={x∈IN/ x|32}
; A={x∈IN/ x|20}
B={x∈IN/ x|14}
(q1) تحقق ان E; A; B⊂L
(q1) حدد B∩Āو B∩Ē و B∩A و B∩E

تصحيح

1) نبين ان B∩Ā=B∩Ē ⇔B∩A=B∩E
نفترض B∩Ā=B∩Ē
x∈B∩A ⇔ x∈B ∧ x∈A
⇔ x∈B ∧ x∉Ā
⇔ x∈B ∧ x∉Ē , (x∈Ē ⇔ x∈Ā)
⇔ x∈B ∧ x∈E
⇔ x∈B∩E
اذن B∩Ā=B∩Ē ⇔B∩A=B∩E

2) (q1) x∈E ⇒ x|32
32|1120 ⇒ x|1120
⇒ x∈L ⇒ E⊂L
لدينا
x∈A ⇒ x|20
20|1120 ⇒ x|1120
⇒ x∈L ⇒ A⊂L
ولدينا
x∈B ⇒ x|14
14|1120 ⇒ x|1120
⇒ x∈L ⇒ B⊂L
(q2) B={x∈IN/ x|14}={1;2;7;14}
E={x∈IN/ x|32}={1;2;4;8;16;32}
B∩E= {1;2} ⇒ B∩Ē={7;14}
A={x∈IN/ x|20}={1;2;4;5;10;20}
B∩A={1;2} ⇒ B∩Ā={7;14}

تمرين 11 tp

E ; F مجموعتان معرفتان كما يلي
E={(x;y)∈IR²/ 1≤ x ≤ 3}
F={(x;y)∈IR²/ x-y+1 ≥ 0 ∧ x-y-2 ≤0}
حدد مبيانيا E∩F

تصحيح

المجموعة E هي مجموعة ازواج احداثيات نقط جزأ المستوى المحصور بين المستقيمين (Δ1): x=1 ; (Δ2): x=3
بالنسبة للمجموعة F ينبغي دراسة اشارة كل من العددين
x-y+1 و x-y-2 ولذلك يجب انشاء المستقيمين (Δ2) و (Δ1) في نفس المعلم
O∉(Δ1) , 0-0+1 > 0 يعني نصف المستوى الذي تخمه (Δ1) ويحتوي على O معرف بالمتراجحة x-y+1≥0
O∉(Δ2) , 0-0-2 < 0 يعني نصف المستوى الذي تخمه (Δ2) ويحتوي على O معرف بالمتراجحة x-y-2≤0

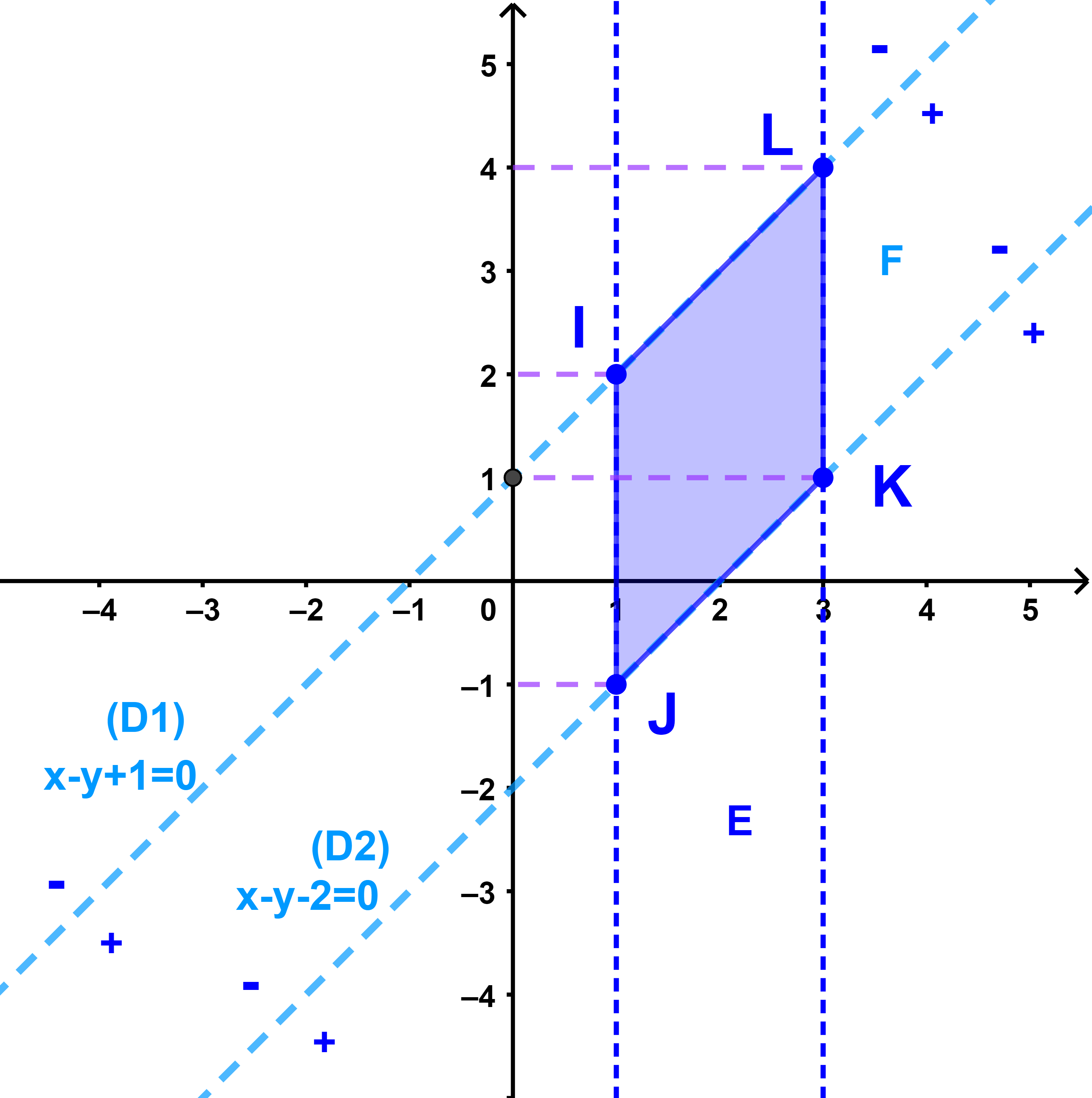
ومنه فان E∩F هي مجموعة ازواج احداثيات نقط جزأ المستوى المحاط بالمتوازي الاضلاع IJKL

تمرين 12 tp

E ; F مجموعتان معرفتان كما يلي
E={(x;y)∈IR²/ x+y+1 > 0}
F={(x;y)∈IR²/ x-y+1 < 0}
حدد مبيانيا E∩F