Exercice 1 tp

Résoudre le système suivant

{	x(y-1)+y-1=0
	x²+x=y+xy

Exercice 2

Soit a∈IR.
On considère le polynome suivant
p(x) = 7ax² + (3-a²)x - 10
on donne p(1)=3 et p(-1)=5.
Déterminer a.

Exercice 3 tp

Soit n∈ℤ
tel que (n²-2n=0) ∧ (n²-4=0)
Déterminer la valeur de n.

Correction

{	n²-2n = 0	⇔ {	n(n-2)=0
	n²-4=0		(n-2)(n+2)=0

⇔ {	n=0 ou n-2 = 0
	n-2=0 ou n+2=0

⇔		n=0 et n=2
	ou	n=0 et n=-2
	ou	n=2 et n=2
	ou	n=2 et n=-2

donc n = 2 ainsi S={2}.

Exercice 4 tp

Résoudre graphiquement le système suivant

(S) {	(x-y)(x+y-2)>0
	-2<x<3

Correction

(S) {	(x-y)(x+y-2)>0
	-2<x<3

(x-y)(x+y-2) >0 ⇔
(x-y>0 et x+y-2>0) ou (x-y<0 et x+y-2<0)
donc (S) ⇔

ou	(x-y> 0) et (x+y-2>0) et (-2<x<3)
	(x-y<0) et (x+y-2<0) et (-2<x<3)

On traçe les deux droites (D1): x-y=0
et (D2): x+y-2=0 dans le même repère.

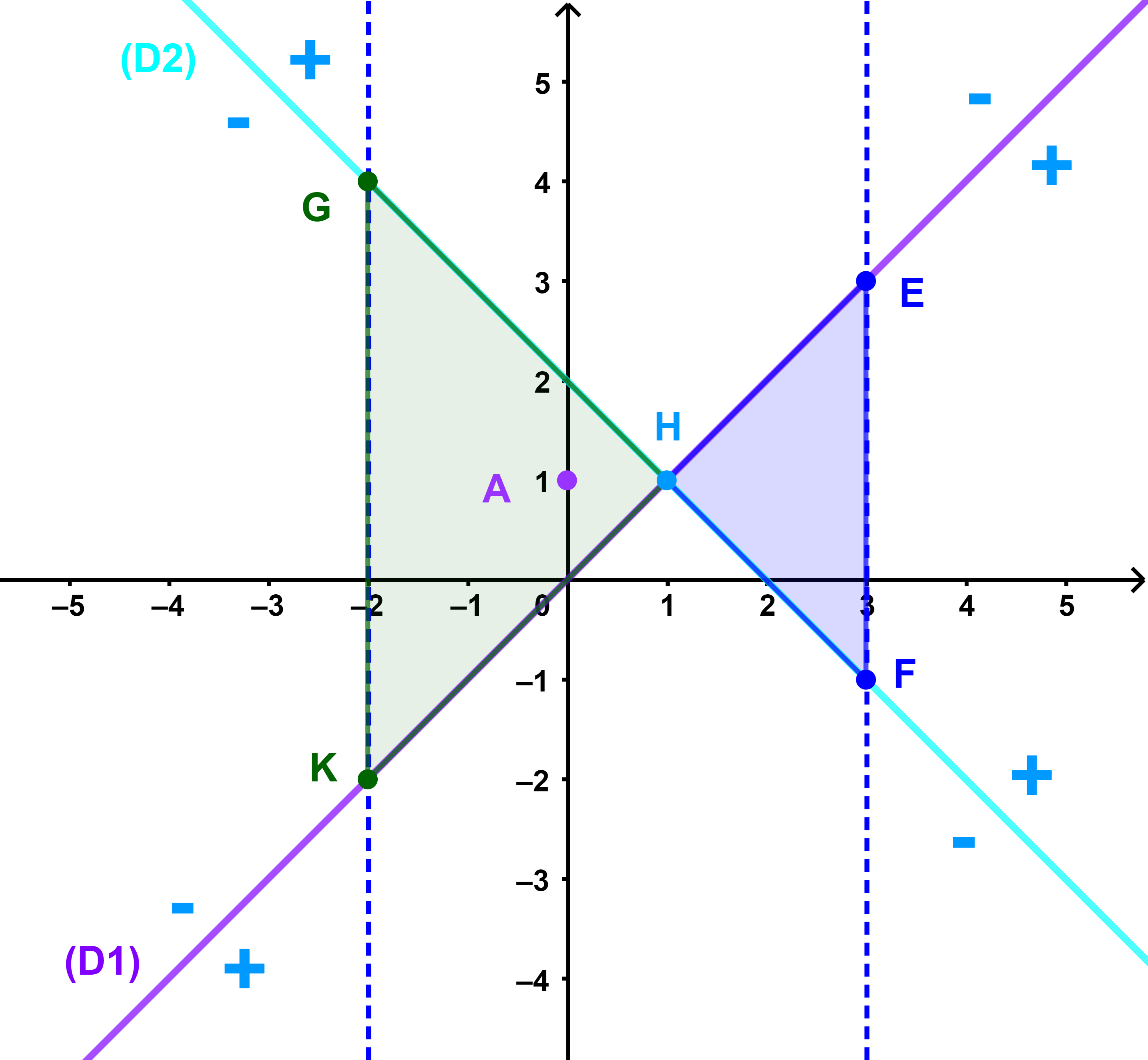
Puis on étudie le signe des nombres
x-y et x+y-2 (régionnement d'un plan).

1) Signe de x-y
on considère un point qui n'appartient pas à (D1) soit A(0;1)
on a 0-1=-1< 0 donc le demi plan dont le bord (D1) contenant le point A est défini par l'inéquation x-y<0.
2) Signe de x+y-2
on considère un point qui n'appartient pas à (D2) soit O(0;0)
On a 0+0-2=-2< 0 donc le demi-plan dont le bord (D2) contenant le point O est défini par l'inéquation x+y-2<0.

Ainsi l'ensemble des solutions du système (1)

{	((x-y>0) ∧ (x+y-2>0))
	-2<x<3

est l'ensemble des couples des coordonnées des points d'une partie ouverte du plan délimitée par le triangle EFH.

L'ensemble des solutions du système (2)

{	((x-y<0) ∧ (x+y-2<0))
	-2<x<3

est l'ensemble des couples des coordonnées de points d'une partie ouverte du plan délimitée par le triangle GHK.

Et donc l'ensemble des solutions du système

∨	((x-y>0) ∧ (x+y-2>0)) ∧ -2<x<3
	(((x-y<0) ∧ (x+y-2< 0)) ∧ -2<x<3

est l'ensemble des couples de coordonnées des points de deux parties ouvertes du plan déterminées par les deux triangles EFH et GHK.