Exercice 1 tp

Soient A: B et E des parties d'un ensemble L.
1) Montrer que B∩Ā=B∩Ē ⇔B∩A=B∩E.
2) Application
L={x∈IN/ x|1120}
E={x∈IN/ x|32}
A={x∈IN/ x|20}
B={x∈IN/ x|14}
(a) Vérifier que E; A; B⊂L.
(b) Déterminer B∩Āet B∩Ē et B∩A et B∩E.

Correction

1) On montre B∩Ā=B∩Ē ⇔B∩A=B∩E
on suppose que B∩Ā=B∩Ē
x∈B∩A ⇔ x∈B ∧ x∈A
⇔ x∈B ∧ x∉Ā
⇔ x∈B ∧ x∉Ē , (x∈Ē ⇔ x∈Ā)
⇔ x∈B ∧ x∈E
⇔ x∈B∩E
donc B∩Ā=B∩Ē ⇔B∩A=B∩E.

2) (a) x∈E ⇒ x|32
32|1120 ⇒ x|1120
⇒ x∈L ⇒ E⊂L
x∈A ⇒ x|20
20|1120 ⇒ x|1120
⇒ x∈L ⇒ A⊂L
x∈B ⇒ x|14
14|1120 ⇒ x|1120
⇒ x∈L ⇒ B⊂L.

(b) B={x∈IN/ x|14}={1;2;7;14}
E={x∈IN/ x|32}={1;2;4;8;16;32}
B∩E= {1;2} ⇒ B∩Ē={7;14}
A={x∈IN/ x|20}={1;2;4;5;10;20}
B∩A={1;2} ⇒ B∩Ā={7;14}.

Exercice 2 tp

Soient E et F deux ensembles définies par
E={(x;y)∈IR²/ x+y+1 > 0}
F={(x;y)∈IR²/ x-y+1 < 0}
Déterminer graphiquement E∩F.

Exercice 3 tp

Soient E et F deux parties de IR² définies par
E={(x;y)∈IR²/ 1≤x≤3}
F={(x;y)∈IR²/ x-y+1≥0 ∧ x-y-2≤0}.
Déterminer graphiquement E∩F.

Correction

E est l'ensemble des couples des coordonnées des points d'une partie du plan délimitée par les droites (Δ₁): x=1 ; (Δ₂): x=3.

Pour l'ensemble F on doit étudier le signe de x-y+1 et x-y-2
et donc les droites (Δ₂) et (Δ₁) doivent êtres tracées sur le même repère.
O∉(Δ₁) 0-0+1>0 signifie que le demi-plan dont le bord est la droite (Δ₁) contenant O est définie par l'inéquation
x-y+1≥0.
O∉(Δ₂) 0-0-2<0 signifie que le demi-plan dont le bord est la droite (Δ₂) contenant O est définie par l'inéquation
x-y-2≤0.

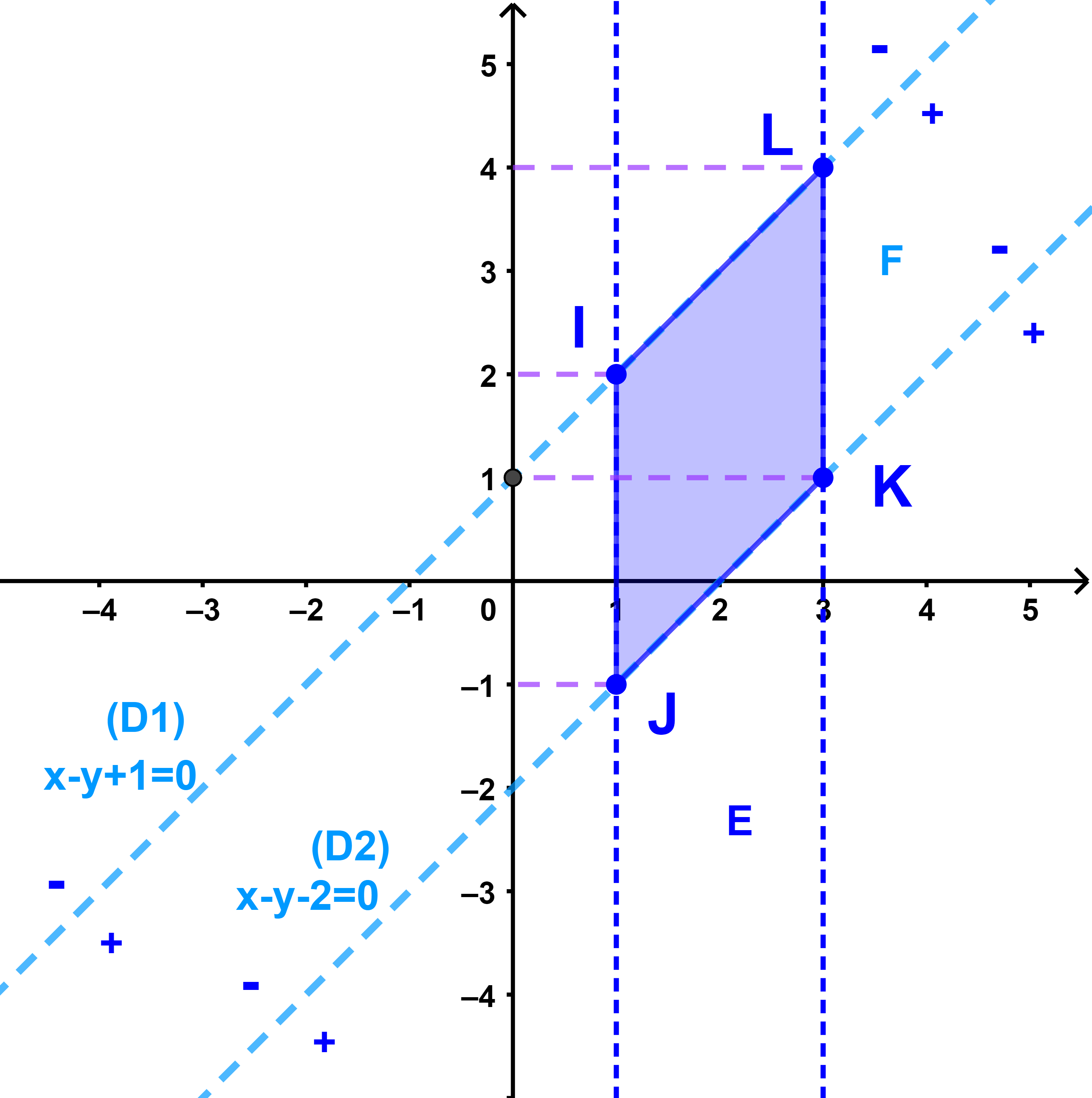
Ainsi E∩F est l'ensemble des couples des coordonnées d'une partie du plan délimitée par le parallélogramme IJKL.

Exercice 4 tp

Soient E et F deux ensembles définis par
E={x∈IR/ 2sin(x)-√(3)=0}
F={x∈IR/ 2cos(x)-1=0}0
Déterminer E∩F et E∪F.