تمرين 13 tp

لتكن E مجموعة قواسم الموجبة للعدد 20
و F مجموعة قواسم الموجبة للعدد 45
1) حدد بادراك كل من المجموعتين E و F
2) حدد بتفصيل E∩F

تصحيح

1) E={x∈IN / x|20}
F={x∈IN / x|45}
2) E∩F={x∈IN / x|20 ∧ x|45}
={x∈IN / x | 20∧45}

20		2			45		3
10		2			15		3
5		5			5		5
1					1		1

20 = 2².5 ; 45 = 3².5
⇒ 20∧45 = 5
اذن E∩F={1;5}

تمرين 14 tp

E ; F مجموعتان معرفتان كما يلي
E={x∈IR/ 2sin(x)- √(3)= 0}
F={x∈IR/ 2cos(x)-1 = 0}
حدد E∩F و E∪F ومثلهما على الدائرة المثلثية

تمرين 15 tp

ليكن f تطبيقا معرفا من المجموعة E نحو المجموعة F
1) بين ان اذا كان f رتيب قطعا على E فانه تبايني
2) بين بمثال مضاد ان العكس خاطئ

تصحيح

1) نفترض ان f رتيب قطعا على E E اي تزايدي قطعا واما تناقصي قطعا على
فليكن تناقصي قطعا على E ونبين انه تبايني E , (نفس العمل في حالة f تزايدي
اي نبين ان ∀(x;y)∈E²: f(x)=f(y) ⇒ x=y
او نبين ان باستعمال الاستدلال المضاد للعكس ∀(x;y)∈E²: x≠y ⇒ f(x)≠f(y)
x≠y ⇒x < y ∨ x > y
فليكن x < y ,(نفس العمل في حالة x > y)
x < y ⇒ f(x) > f(y) ,( f تناقصي قطعا)
f(x) > f(y) ⇒ f(x)≠f(y)
اذن ∀(x;y)∈E²: x≠y ⇒ f(x)≠f(y)
وهذا يعني ان f تبايني

2) العكس خاطئ نأخذ مثالا مضادا
E={-2;-1;5} ; F={1;4;10;25}

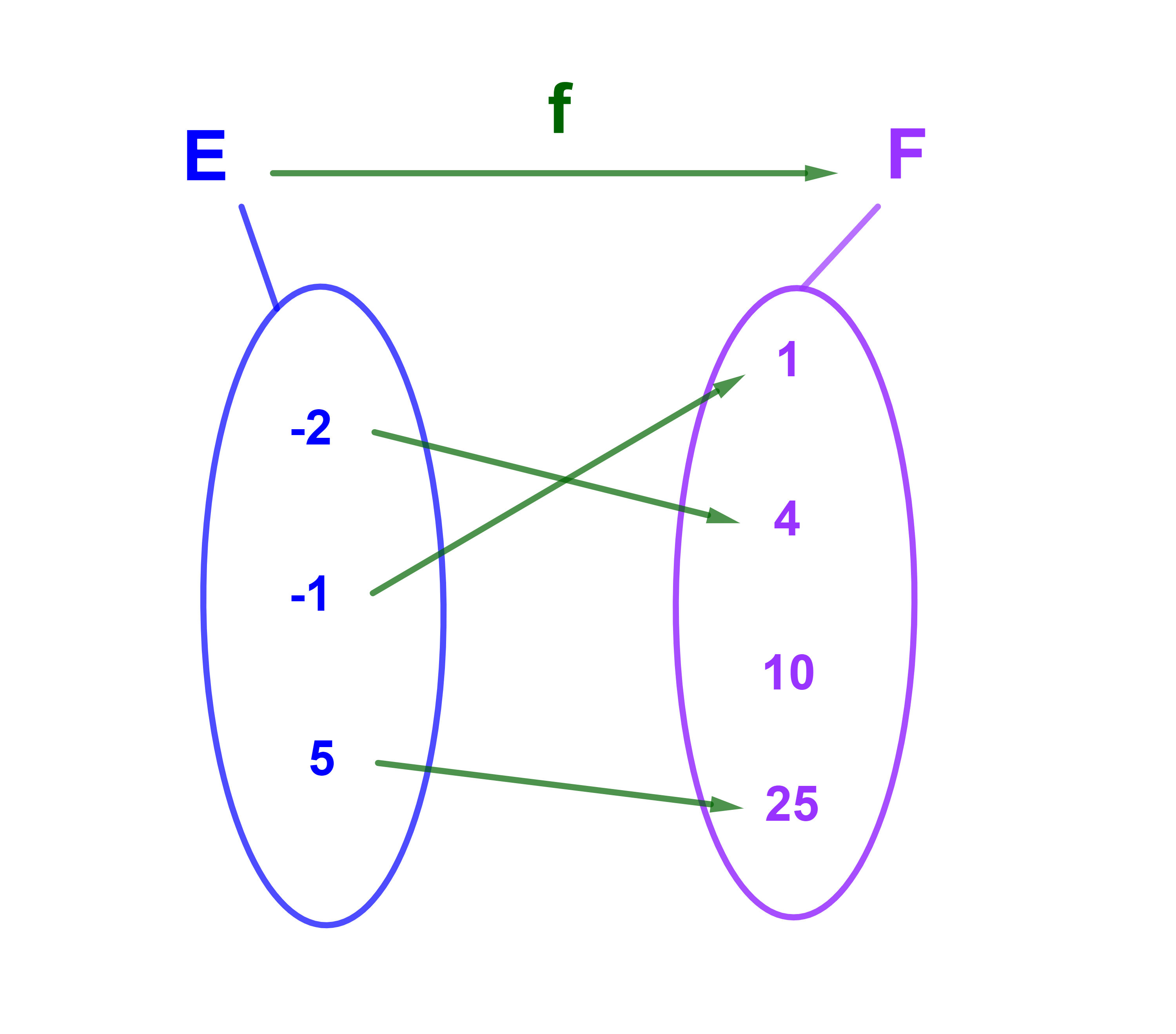
f تطبيق تبايني
لدينا
-2 < -1 و f(-2) > f(-1)
ولدينا
-1 < 5 و f(-1) < f(5)
اذن f ليست رتيبة على E

تمرين 16 tp

ليكن f تطبيقا معرفا من E=]-1;+∞[ نحو F=]-∞;2[ ومعرفا كما يلي

f(x) =	2x
	x+1

بين ان f تطبيق تقابلي من E نحو F

تصحيح

(∀y∈F) (∃!x∈E)/ f(x)=y ?
لدينا
y∈F ⇒ y < 2 ⇒ y≠2

y=	2x	⇔ 2x = y(x+1) ⇔ x(2-y)=y
	x+1
⇒ x =	y	, y ≠ 2
	2-y

العنصر x وحيد يبقى التأكد اذا كان ينتمي الى المجموعة E
ندرس اشارة العدد x

y	-∞		0		2
x		-	0	+		||

اذا كان 0 ≤ y < 2 فان x≥0 ومنه فان x∈E
واذا كان y < 0 فان x < 0 , (2-y > 0)
نفترض ان x∉E
وهذا يعني ان

x =	y	< -1 ⇒ y < -(2-y) ⇒ 0 < -2
	2-y

وهذا غير ممكن ومنه فان
(∀y∈F) (∃!x∈E)/ f(x)=y
وبالتالي f تقابل من E نحو F

ملاحظة التطبيق التالي

F →	E
x →	x
	2-x

المعرف من F نحو E يسمى التقابل العكسي للتقابل f

تمرين 17 tp

ليكن f تطبيق معرف من E=[1;+∞[ نحو E بما يلي
f(x)=2√(x-1) +x
بين ان f تقابل من E نحو E

تصحيح

لدينا
D={x∈IR / x-1≥0}=E
(∀y∈E) (∃!x∈E)/ f(x)=y ?
لدينا
f(x)=y ⇔ 2√(x-1) +x = y

⇔ (x-1)+2√(x-1)+1 = y
⇔ (√(x-1) + 1)² = y
⇔ |√(x-1) + 1| = √(y) , (y≥1 > 0)
⇔ √(x-1) = √(y)-1 ≥ 0 , (y≥1)
⇔ x-1 = (√(y)-1)²
⇔ x = (√(y)-1)² + 1
اذن العنصر x موجود وينتمي الى المجموعة E لان (√(y)-1)² + 1 ≥ 1
ملاحظة التطبيق التالي x→ (√(x) - 1)² + 1
المعرف من E نحو E يسمى التقابل العكسي للتقابل f