Etude des fonctions numériques (17)
Exercice 1 tp
Soit f une fonction définie par
| f(x) = | 2cosx - 1 |
| cosx - 2 |
et (C) sa courbe dans un repère (O;i→;j→).
1) Déterminer D, le domaine de définition de f.
2) Montrer que f est périodique et paire puis
déterminer J le domaine réduit d'étude de f.
2) Montrer que ∀x∈J
| f '(x) = | 3sinx |
| (cosx - 2)² |
3) Etudier la monotonie de f et tracer son tableau de variations sur [-π;π].
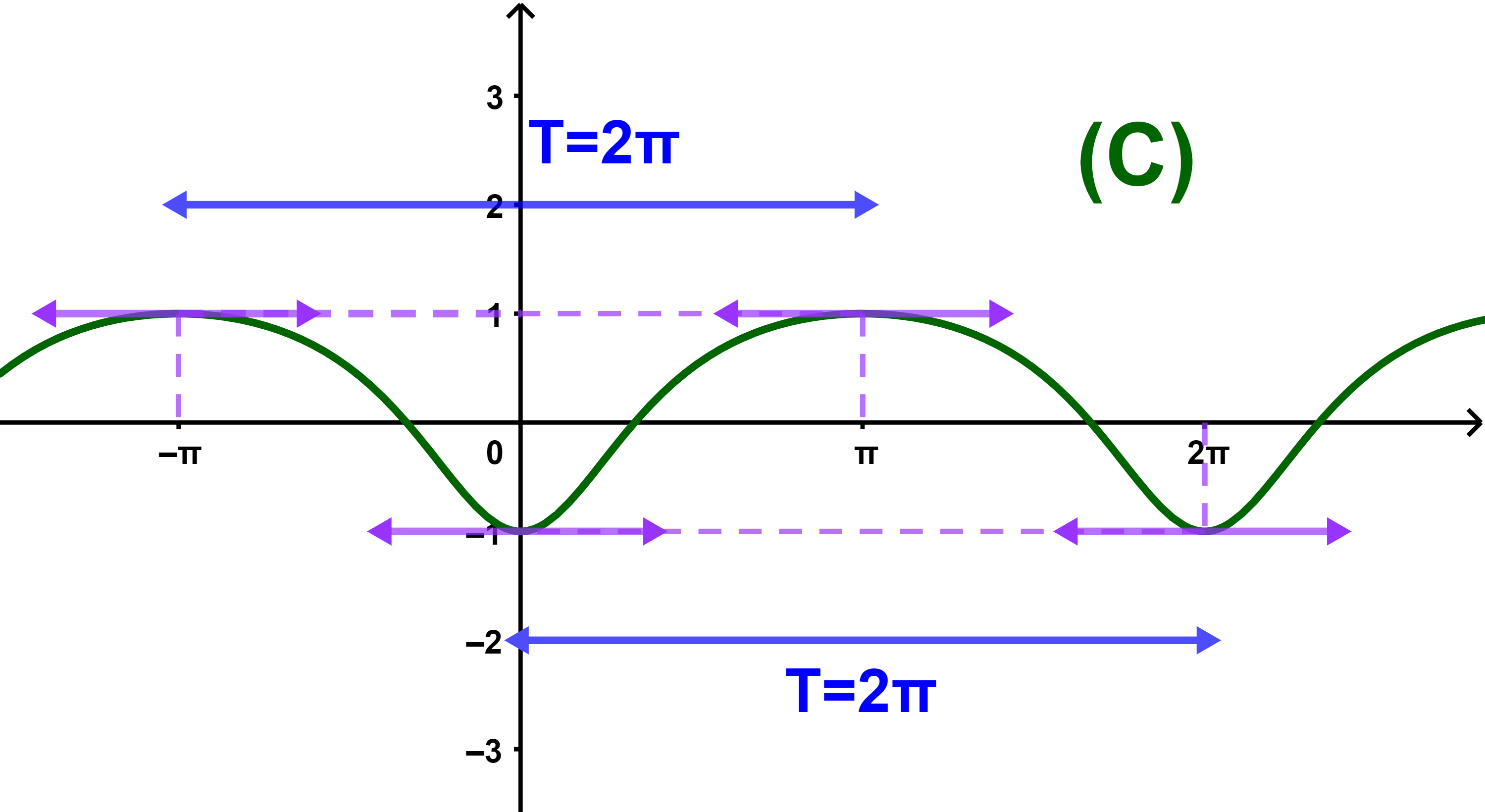
4) Tracer la courbe de f sur [-π;2π].
Correction
1) D={x∈IR / cosx - 2 ≠0}.
On a (∀x∈IR) -1≤cosx ≤1 donc cosx≠2
ainsi D=IR.
On a (∀x∈IR): x+2π;x-2π∈IR.
| f(x+2π) = | 2cos(x+2π)-1 |
| cos(x+2π) - 2 | |
| = | 2cos(x) - 1 |
| cos(x) - 2 |
donc f(x+2π)=f(x) et cela signifie que f est périodique de période 2π ey il suffit donc de l'étudier sur un intervalle d'amplitude 2π.
Soit I=[-π;π] ou [0;2π]
et puisque l'étude de la parité de f dans ce qui suit, il est nécessaire de choisir un intervalle centré.
Nous choisissons donc l'intervalle
I=[-π;π].
I est centré en 0
donc (∀x∈I) on a (-x)∈I.
| f(-x) = | 2cos(-x) - 1 |
| cos(-x) - 2 | |
| = | 2cos(x) - 1 |
| cos(x) - 2 |
Donc f(-x)=f(x)
alors f est paire et J=[0;π] son domaine réduit d'étude.
2) cos est dérivable sur IR en particulier sur J
x→(2cosx -1) est dérivable sur J
et x→(cosx - 2) est dérivable sur J et ne s'annule pas donc f est dérivable sur J. Soit x∈J
| f '(x) = | -2sinx(2cosx - 2)- (-sinx)(2coxx - 1) |
| (cosx - 2)² |
| = | 4sinx + sinx |
| (cosx - 2)² |
ainsi
| f '(x) = | 3sinx |
| (cosx - 2)² |
f'(x)=0 ⇔ sinx=0
⇔ x=kπ tel que k∈ℤ
puisque x∈J alors x=0 ou x=π
(∀x∈J) on a sinx ≥ 0.
Donc (∀x∈J\{0;π}): f'(x)>0
ainsi f est strictement croissante sur J
et puisque f est paire alors elle est strictement décroissante sur [-π;0].
| x | -π | 0 | π | |||
| f '(x) | 0 | + | 0 | + | 0 | |
| f | 1 | ↘ |
-1 |
↗ |
1 |
4) On trace (C) sur J et on la compléte sur I en utilisant la symétrie axiale d'axe l'axe des abscisses puis la translation T2πi→.