Etude des fonctions numériques (18)
Exercice 1 tp
Soit f une fonction définie par
f(x)=sin(2x)+2cos(x)
et (C) sa courbe dans un repère (O;i→;j→).
1) Montrer que f est périodique et déterminer J le domaine réduit d'étude de f .
2) Etudier la monotonie de f et tracer son tableau de variations sur [0;2π].
3) Résoudre algébriquement et graphiquement l'équation f(x)=0 sur[0;;3π].
Voila la courbe de la fonction f.

Exercice 2 tp
Soit f une fonction définie par
f(x) = 2x-2 +√(x-1).
et (C) sa courbe dans un repère orthonormé
1) Calculer la limite de f en +∞ puis déterminer une direction asymptotique de (C).
2) Etudier la dérivabilité de f au point 1.
3) Etudier la monotonie de f et tracer son tableau de variations.
4) Tracer la courbe (C).
Exercice 3 tp
On considère une fonction f définie par
| f(x) = x + | | x²+1 | | |
| x²-1 |
et (C) sa courbe dans un repère orthonormé.
1) Calculer les limites suivantes
lim (-1) |
f(x) | lim 1 |
f(x) |
lim -∞ |
f(x) | lim +∞ |
f(x) |
2) Déterminer les asymptotes de (C).
3) Calculer f'(x) quand x∈]-∞;-1[∪]1;+∞[
et f'(x) quand x∈]-1;1[.
4) Utiliser la courbe (C) ci-jointe
pour étudier la monotonie de f et tracer son tableau de variations.
5) Soit (C) la courbe ci dessous.
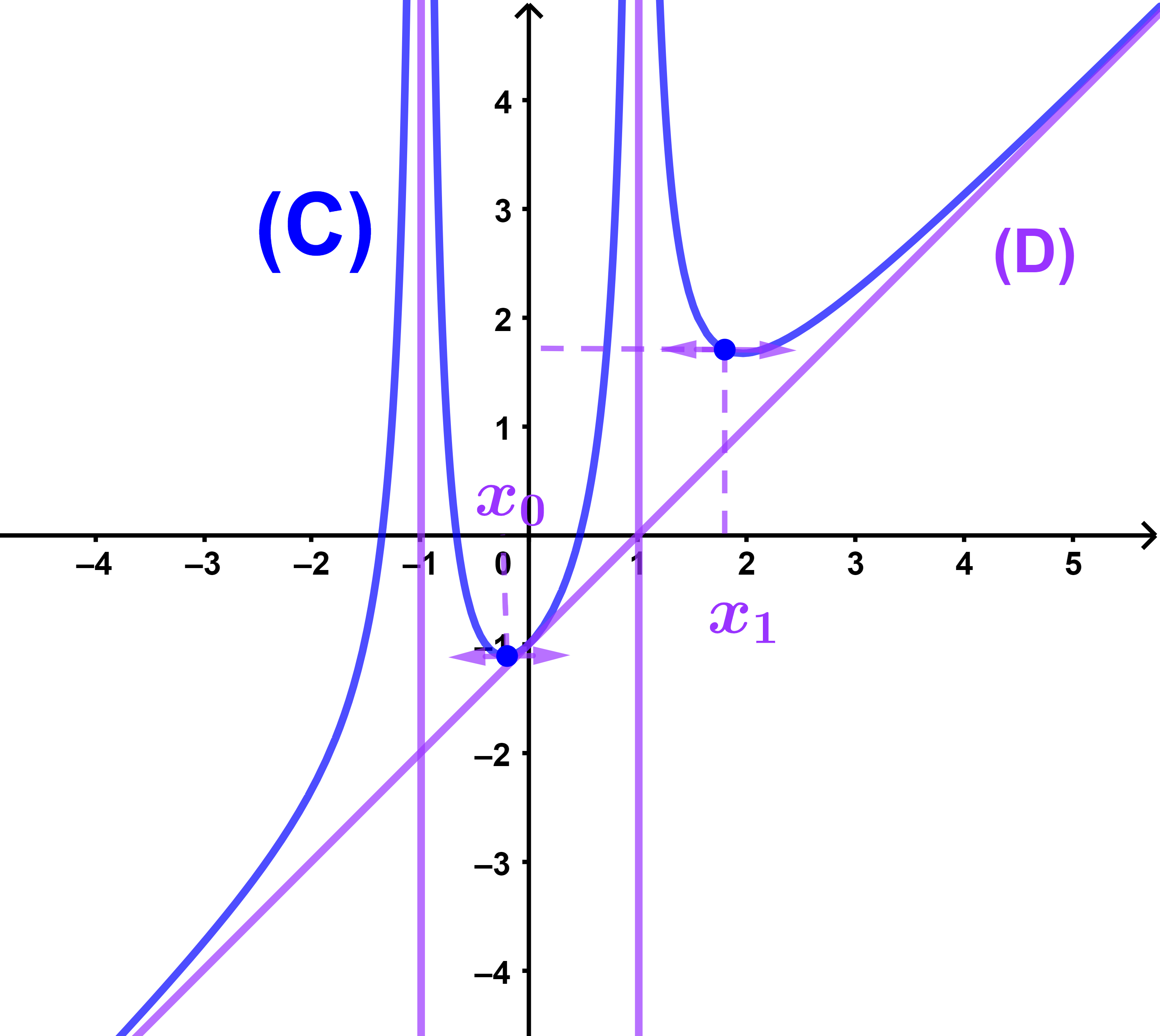
(a) Résoudre graphiquement et selon la paramètre m l'équation f(x)=m.
(b) Etudier graphiquement le signe de la fonction f.