تمرين 1 tp

لتكن f دالة عددية معرفة كالتالي f(x)=x³-3x
1) حدد مركز تماثل منحنى الدالة f
2) حدد مجال الدراسة المختصر للدالة f
3) ادرس رتابة الدالة f وانشئ جدول تغيراتها
4) انشئ منخنى الدالة f في معلم متعامد ممنظم

تمرين 2 tp

لتكن f دالة عددية معرفة كالتالي

f(x)=	1	x³-2x²+3x-2
	3

1) احسب النهايات عند محدات مجموعة تعريف الدالة f

2) حدد الفرعين اللانهائيين للدالة f
3) (q1) ادرس رتابة الدالة f وانشئ جدول التغيرات
(q2) استنتج مطارف الدالة f
4) انشئ منحنى الدالة f في معلم متعامد ممنظم
5) (q1) حل مبيانيا المعادلة f(x)=0
(q2) (q1) حل مبيانيا المتراجحة f(x) < 0

تصحيح

1) D=IR

lim -∞	f(x)=	lim -∞	1	x³= - ∞
			3
lim +∞	f(x)=	lim +∞	1	x³= + ∞
			3

2) لدينا lim_-∞f(x)= - ∞

lim -∞	f(x)	=	lim -∞	x³	=	lim -∞	x²	= + ∞
	x			3x			3

اذن المنحنى (C) يقبل فرعا شلجميا في اتجاه محور الاراتيب بجوار -∞
ولدينا lim_+∞f(x)=+∞

lim +∞	f(x)	=	lim +∞	x³	=	lim +∞	x²	= + ∞
	x			3x			3

اذن المنحنى (C) يقبل فرعا شلجميا في اتجاه محور الاراتيب بجوار +∞
3) (q1) الدالة f حدودية اذن قابلة للاشتقاق على IR
f '(x)=x²-4x+3 f '(x)=0⇔(x-1)(x-3)=0
⇔x=1 ∨ x=3
وبما ان a=1>0 فان الدالة f تزايدية قطعا على ]-∞;1] و [3;+∞[ وتناقصية قطعا على [1;3]

x	-∞		1		3		+∞
f'(x)		+	0	-	0	+
f	-∞	↗	-2/3	↘	-2	↗	+∞

(q2) لدينا f تزايدية قطعا على ]-∞;1] وتناقصية قطعا على [1;3] اذن -2/3 قيمة قصوى للدالة f عند1
لدينا f تناقصية قطعا على [1;3] وتزايدية قطعا على [3;+∞[ اذن -2 قيمة دنيا للدالة f عند3
4) المنحنى

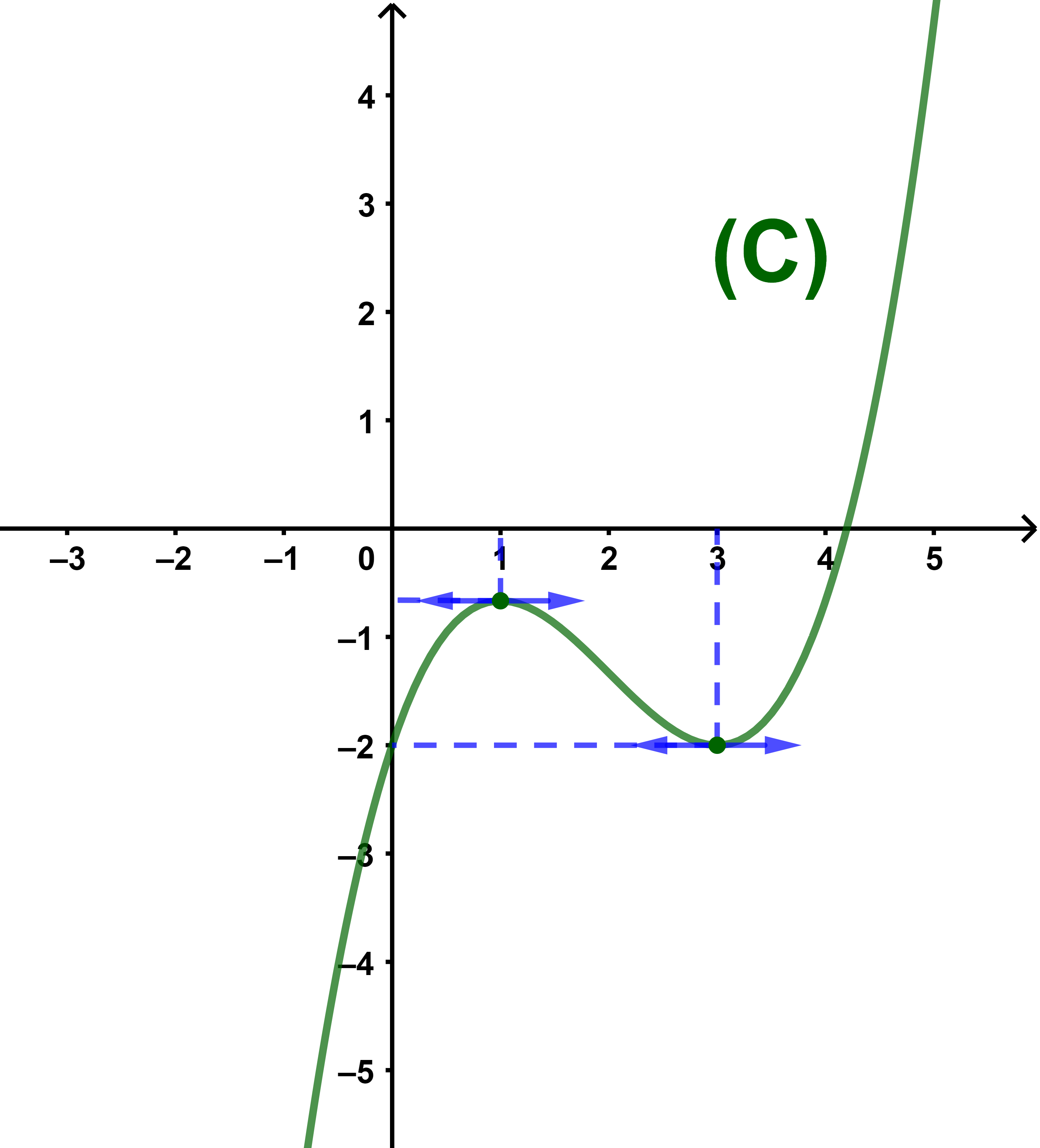
5) (q1) المنحنى يقطع محور الافاصيل في نقطة واحدة اذن المعادلة تقبل حلا واحدا نرمز له ب α ومن الشكل 4< α < 5
(q2) الحل المبياني للمتراجحة f(x)< 0 هو مجموعة افاصيل نقط المنحنى الموجودة تحت محور الافاصيل وبذلك S=]-∞;α[

تمرين 3 tp

لتكن f دالة عددية معرفة كالتالي

f(x)=x+1+	1
	x

1) احسب النهايات عند محدات مجموعة تعريف الدالة f
2) حدد مقاربات الدالة f
3) ادرس رتابة الدالة f وانشئ جدول التغيرات
4) انشئ منحنى الدالة f في معلم متعامد ممنظم

تمرين 4 tp

لتكن f دالة عددية معرفة كالتالي

f(x)=	x4+1
	x4-1

1) احسب النهايات عند محدات مجموعة تعريف الدالة f
2) حدد مقاربات الدالة f
3) ادرس رتابة الدالة f وانشئ جدول التغيرات
4) انشئ منحنى الدالة f في معلم متعامد ممنظم