Etude des fonctions numériques (1)
Exercice 1 tp
Soit f une fonction définie par
| f(x) = | 1 | x³-2x²+3x-2 |
| 3 |
et (C) sa courbe dans un repère orthonormé (O;i→;j→).
1) Calculer les limites suivantes
lim -∞ |
f(x) | lim +∞ | f(x) |
2) Déterminer les branches infinies de (C).
3) (a) Etudier la monotonie de f et tracer son tableau de variations.
(b) Déduire les extremums de f.
4) Tracer la courbe (C) et résoudre graphiquement l'inéquation f(x)≤0.
Correction
1) f est un polynôme donc D=IR.
lim -∞ |
f(x) = | lim -∞ |
1 | x³= - ∞ |
| 3 | ||||
lim +∞ |
f(x) = | lim +∞ |
1 | x³= + ∞ |
| 3 |
2) Branches infinies. On a
lim -∞ |
f(x) = -∞ |
lim -∞ |
f(x) | = | lim -∞ |
x³ | = | lim -∞ |
x² |
| x | 3x | 3 |
donc
lim -∞ |
f(x) | = +∞ |
| x |
ainsi (C) admet une branche parabolique de direction l'axe des ordonnées au voisinage de -∞.
On a
lim +∞ |
f(x) = +∞ |
lim +∞ |
f(x) | = | lim +∞ |
x³ | = | lim +∞ |
x² |
| x | 3x | 3 |
donc
lim +∞ |
f(x) | = + ∞ |
| x |
ainsi (C) admet une branche parabolique de direction l'axe des ordonnées au voisinage de +∞.
3) (a) f est un polynôme donc dérivable sur IR. Soit x∈IR
f'(x)=x²-4x+3.
f'(x)=0 ⇔ (x-1)(x-3)=0
⇔ (x=1 ou x=3)
et puisque a=1>0 alors f est strictement croissante sur ]-∞;1]
strictement croissante sur [3;+∞[ et strictement décroissante sur [1;3].
| x | -∞ | 1 | 3 | +∞ | |||
| f'(x) | + | 0 | - | 0 | + | ||
| f | -∞ |
↗ |
-2/3 | ↘ |
-2 |
↗ |
+∞ |
(b) f est strictement croissante sur ]-∞;1]
et strictement décroissante sur[1;3]
donc (-2/3) est une valeur maximale de f en 1.
f est strictement décroissante sur [1;3]
et strictement croissante sur [3;+∞[
donc -2 est une valeur minimale de f en 3.
4) la courbe
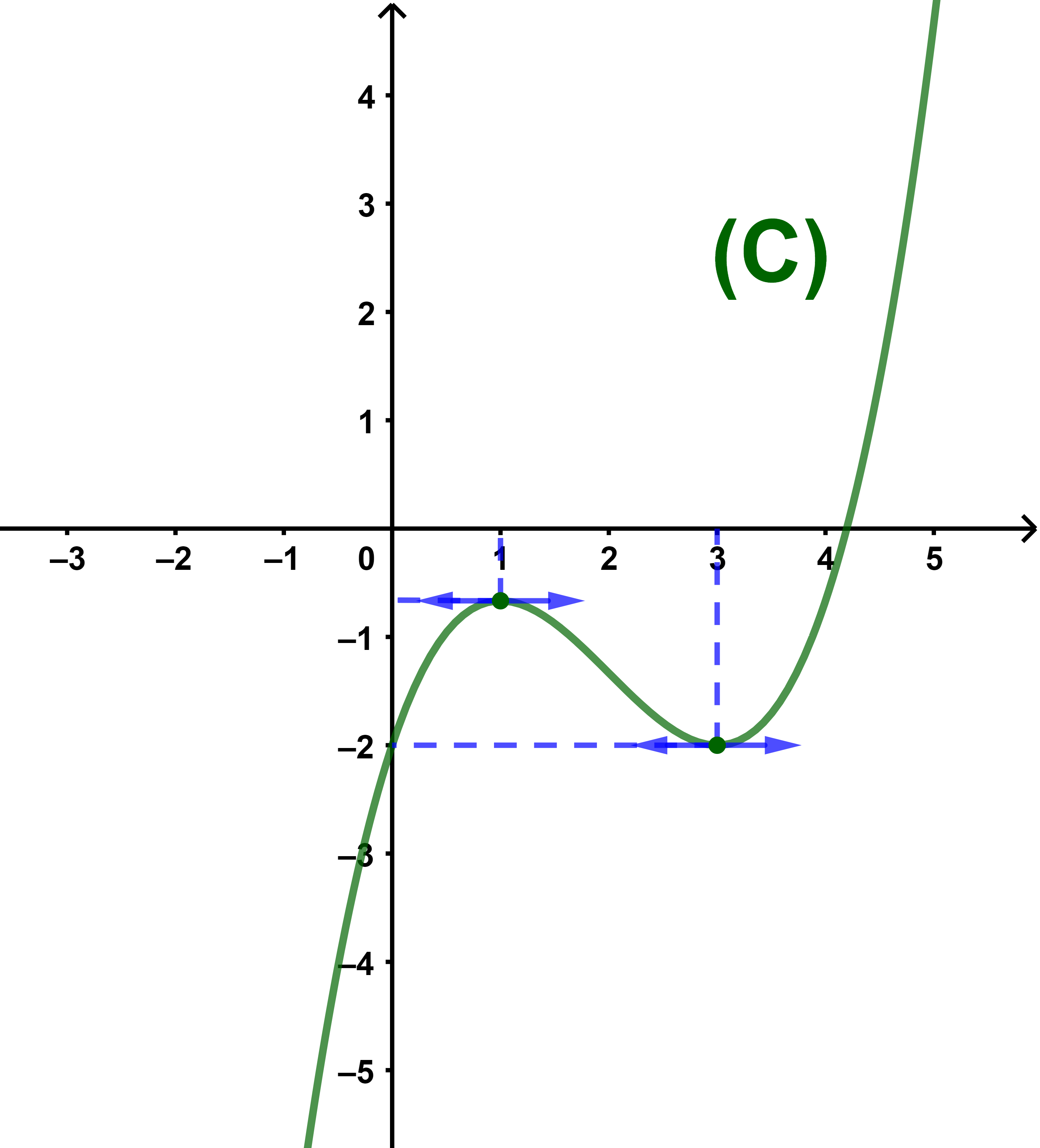
La courbe (C) coupe l'axe des abscisses en un seul point donc l'équation admet une seule solution α tel que
4<α<5.
(b) L'ensemble des solutions de l'inéquation f(x)<0 est l'ensemble des abscisses des points de la courbe qui sont au dessous de l'axe des abscisses.
ainsi S=]-∞;α[.