تمرين 8 tp

لتكن f دالة عددية معرفة كالتالي

1) احسب النهايات عند محدات مجموعة تعريف الدالة f
2) حدد مقاربات منحنى الدالة f
3) ادرس رتابة الدالة f وانشئ جدول التغيرات
4) انشئ منحنى الدالة f في معلم متعامد ممنظم
5) حل مبيانيا المتراجحة f(x) < 0

تصحيح

D={x∈IR / x-1≠0} =]-∞;1[∪]1;+∞[

اولا نكتب f(x) بدون استعمال القيمة المطلقة

{	f(x)= x-1+	1	; x< 1
		x-1
	f(x)= -x+1+	1	; x> 1
		x-1

1) لدينا

اذن	lim ±∞	1	= 0
		x-1

lim -∞	f(x)=	lim -∞	x-1= - ∞
lim +∞	f(x)=	lim +∞	-x+1= - ∞

نحدد النهاية عند 1 بما ان f غير معرفة في 1 ندرس اشارة x-1 بجوار العدد 1

x	-∞		1		+∞
f(x)		-	||	+

lim 1+	1	= +∞ لدينا
	x-1

lim 1+	f(x) =	lim 1+	-x+1 +	1	= 0+∞=+∞
				x-1

lim 1-	1	= - ∞ لدينا
	x-1

lim 1-	f(x) =	lim 1-	x-1 +	1	= 0-∞=-∞
				x-1

2) نحدد مقاربات الدالة f
لدينا

lim 1-

f(x)= -∞

اذن منحنى الدالة f يقبل مقارب معادلته x=1 على يسار 1
لدينا

lim 1+

f(x)= +∞

اذن منحنى الدالة يقبل مقارب معادلته x=1 على يمين 1
لدينا

lim +∞	f(x)-(-x+1)	lim +∞	1	= 0
			x-1

اذن منحنى الدالة f يقبل مقاربا مائلا معادلته y=-x+1 بجوار +∞
لدينا

lim -∞	f(x)-(x-1)	lim -∞	1	= 0
			x-1

اذن منحنى الدالة f يقبل مقاربا مائلا معادلته y=x-1 بجوار -∞
3) ندرس رتابة الدالة f على المجال ]-∞ ; 1[

f(x)= x-1+	1	; x< 1
	x-1
f'(x)= 1-	1	=	x(x-2)
	(x-1)²		(x-1)²

f'(x)=0⇔x(x-2)=0⇔x=0 ∨ x=2
2∉]-∞; 1[ اذن x=0
f تزايدية قطعا على ]-∞;0[ وتناقصية قطعا على [0; 1[; (بين الجذرين)
ندرس رتابة الدالة f على المجال ]1;+∞[

f(x)= -x+1+	1	; x> 1
	x-1
f'(x)= -1-	1
	(x-1)²

∀x∈]1;+∞[; f'(x)< 0 اذن f تناقصية قطعا على ]1;+∞[

x	-∞		0		1			+∞
f'(x)		+	0	-			-
f	-∞	↗	-2	↘	-∞	+∞	↘	-∞

4) المنحنى

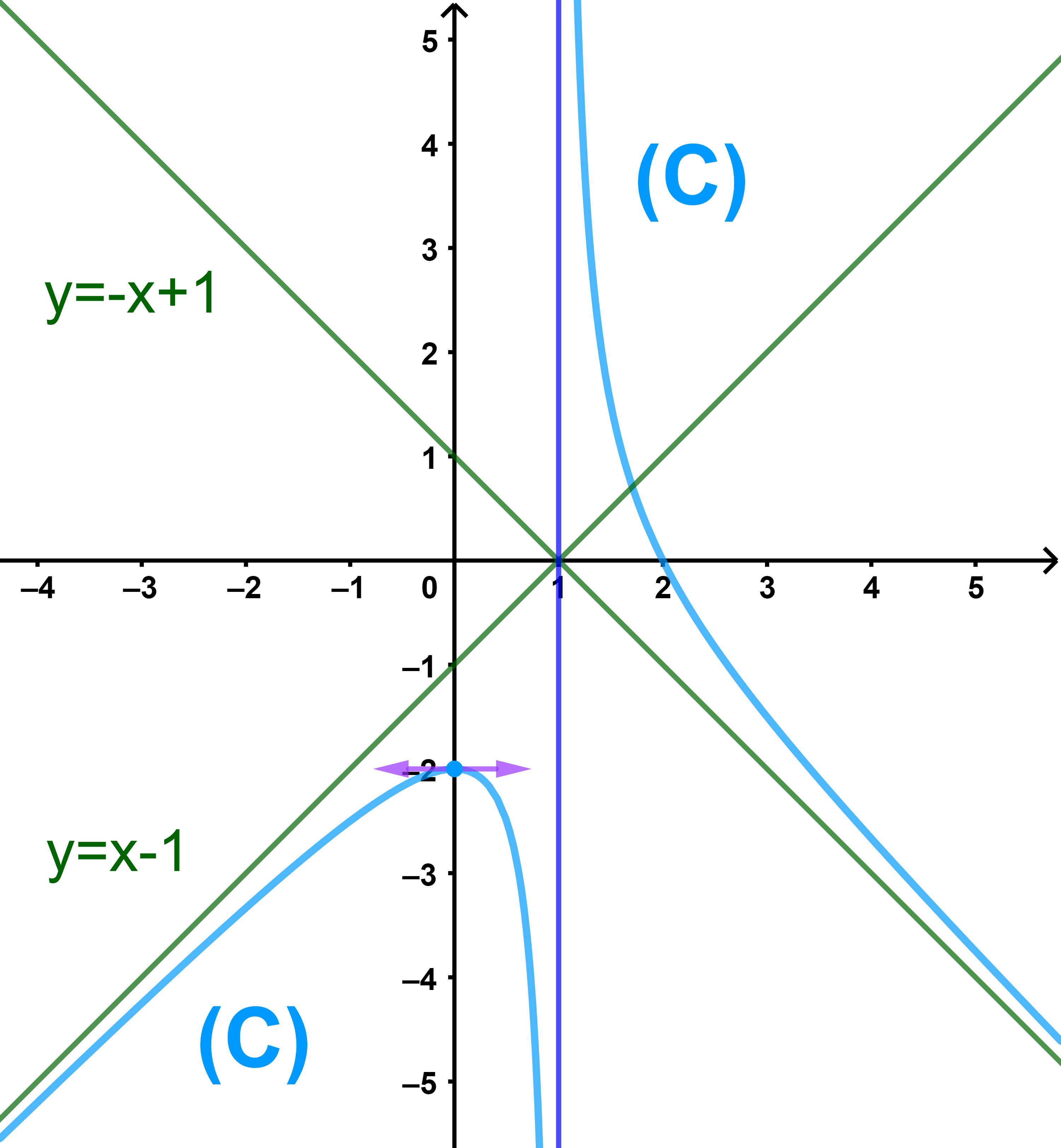
5) المنحنى يقطع محور الافاصيل في نقطة واحدة اذن المعادلة تقبل حلا واحدا نرمز له ب α=2 ومن الشكل
الحل المبياني للمتراجحة f(x)< 0 هو مجموعة افاصيل نقط المنحنى الموجودة تحت محور الافاصيل وبذلك
S=]-∞;1[∪]2;+∞[