تمرين 12 tp

نعتبر الدالة f المعرفة ب

f(x)=	x
	√(|x+1|)

1) احسب نهايات الدالة f عند محدات مجموعة تعريفها ثم حدد مقاربا للمنحنى (C)
2) احسب f'(x) ثم ادرس اشارتها على مجموعة تعريفها وانشئ جدول تغيراتها
3) انشئ منحنى الدالة f في معلم متعامد ممنظم
4) حل مبيانيا وحسب قيم العدد m المعادلة f(x)=m

تصحيح

1) D={x∈IR/ |x+1|> 0} ={x∈IR/ x+1≠0}
=]-∞;-1[∪]-1;+∞[
اولا نكتب f(x) بدون استعمال القيمة المطلقة

{	f(x)=	x	; x< -1
		√(-x-1)
	f(x)=	x	; x> -1
		√(x+1)

lim -∞	x	=	lim -∞	x√(-x-1)
	√(-x-1)			-x-1
=	lim -∞	x	lim -∞	√(-x-1)
		-x-1
=	lim -∞	x	lim -∞	√(-x-1)
		-x

lim -∞

f(x)=

=-1.(+∞)= - ∞

lim +∞	x	=	lim +∞	x√(x+1)
	√(x+1)			x+1

=	lim +∞	x	lim +∞	√(x+1)
		x+1

=	lim +∞	x	lim +∞	√(x+1)
		x

lim +∞

f(x)=

=1.(+∞)= + ∞

|x+1|≥0 اذن lim|x+1|≥0 ومنه فان lim√(|x+1|)≥0

lim -1	x	=	-1	- ∞
	√(|x+1|)		0+

lim -1

f(x)=

= - ∞ اذن

وهذا يعني ان منحنى الدالة f يقبل مقاربا معادلته x=-1
ملاحظة: يمكن تحديد نهاية f عند -1⁺ وعند -1^-

lim -∞

f(x)= - ∞ لدينا

lim -∞	f(x)	=	lim -∞	x
	x			x√(-x-1)
=	lim -∞	1	=	0
		√(-x-1)

وهذا يعني ان منحنى الدالة f يقبل فرعا شلجميا في اتجاه محور الافاصيل بجوار - ∞

lim +∞

f(x)= + ∞ لدينا

lim +∞	f(x)	=	lim +∞	x
	x			x√(x+1)
=	lim +∞	1	=	0
		√(x+1)

وهذا يعني ان منحنى الدالة f يقبل فرعا شلجميا في اتجاه محور الافاصيل بجوار + ∞
2) ندرس رتابة الدالة f على المجال ]-∞;-1[

f(x)=	x	; x< -1
	√(-x-1)

x→(-x-1) موجبة قطعا على المجال I1 وقابلة للاشتقاق على IR وبالخصوص على I1 وكذلك الدالة x→x قابلة للاشتقاق على I1 وبالتالي f قابلة للاشتقاق على I1

f '(x)=	√(-x-1) - x(√(-x-1))'
	(√(-x-1))²
=	2(√(-x-1))² + x
	2(-x-1)√(-x-1)

اذن

f '(x) =	-x-2
	2(-x-1)√(-x-1)

لدينا اشارة f'(x) هي اشارة -x-2
f'(x)=0⇔ -x-2=0⇔x=-2
f تزايدية قطعا على ]-∞;-2] وتناقصية قطعا على [-2;-1[
ندرس رتابة الدالة f على المجال ]-1;+∞[

f(x)=	x	; x> -1
	√(x+1)

لدينا x→(x+1) موجبة قطعا على المجال I2 وقابلة للاشتقاق على IR وبالخصوص على I2 وكذلك الدالة x→x قابلة للاشتقاق على I2 وبالتالي f قابلة للاشتقاق على I2

f '(x)=	√(x+1) - x(√(x+1))'
	(√(x+1))²

=	2(√(x+1))² - x
	2(x+1)√(x+1)
=	x+2
	2(x+1)√(x+1)

لدينا اشارة f'(x) هي اشارة x+2
f'(x)=0⇔ x+2=0⇔x=-2
-2∉I2 و x+2>0 وبالتالي f تزايدية قطعا على ]-1;+∞[

x	-∞		-2		-1				+∞
f'(x)		+	0	-				+
f	-∞	↗	-2	↘	-∞		-∞	↗	+∞

3) المنحنى

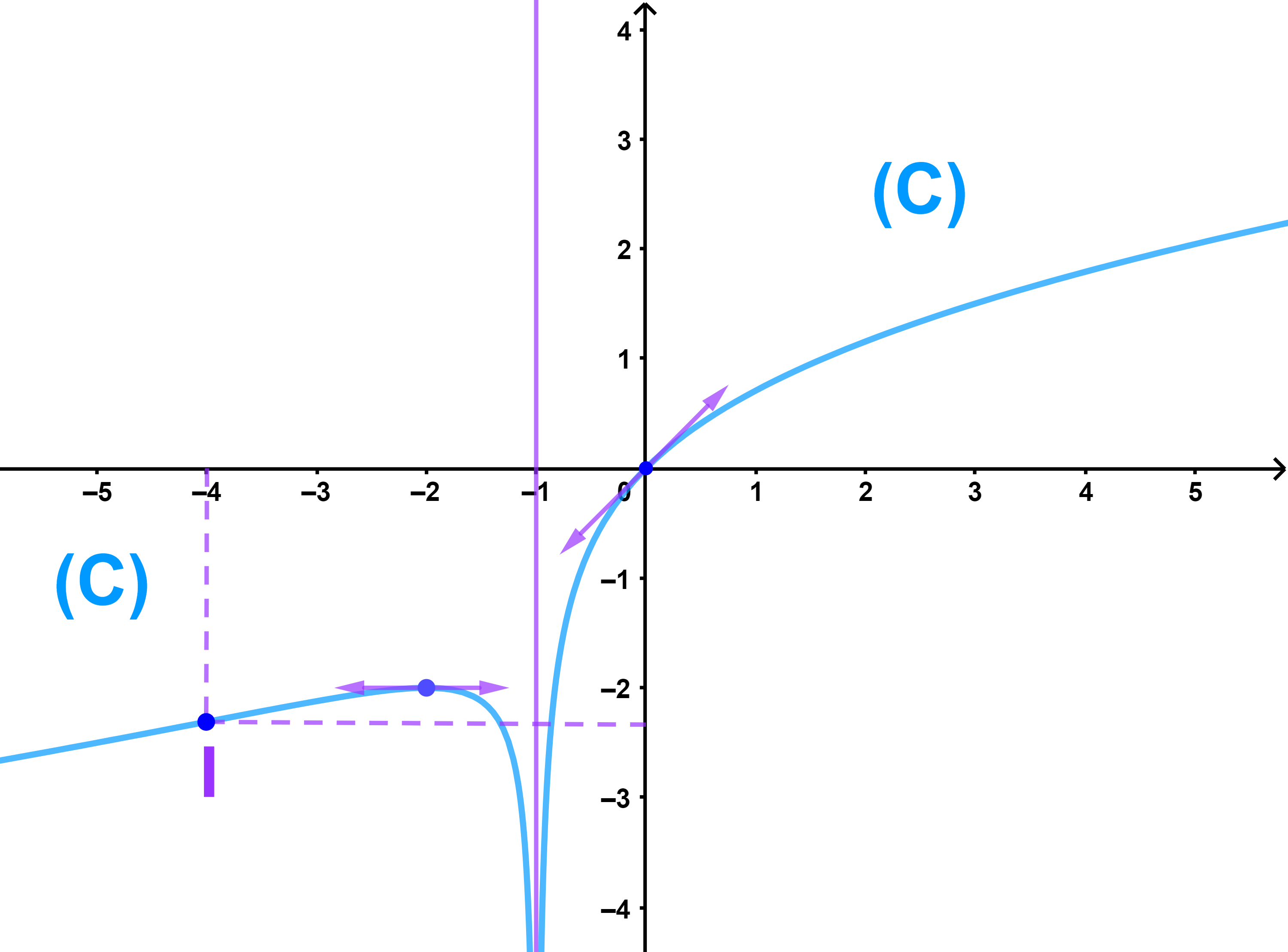
4) نحل مبيانيا وحسب قيم العدد m المعادلة (E): f(x)=m
لذلك نعتبر المستقيم المتغير والموازية لمحور الاراتيب ونرمز له ب (Dm)
اذا كان m<-2 فان (Dm) يقطع المنحنى في ثلاث نقط ومنه فان المعادلة (E) تقبل ثلاث حلول
اذا كان m=-2 فان (Dm) يقطع المنحنى في نقطتين ومنه فان المعادلة (E) تقبل حلين
اذا كان m>-2 فان (Dm) يقطع المنحنى في نقط واحدة ومنه فان المعادلة (E) تقبل حلا واحدا