Généralités sur les fonctions (10)
3.2 La fonction: x→ax³
3.2.1 Propriété
Soit f une fonction définie par f(x)=ax³ avec a≠0 et (C) sa courbe représentative dans un repère (O;i→;j→). f est impaire et de plus
si a>0 alors f est strictement croissante sur IR.
si a<0 alors f est strictement décroissante sur IR.
la courbe (C) est symétrique par rapport à l'origine.
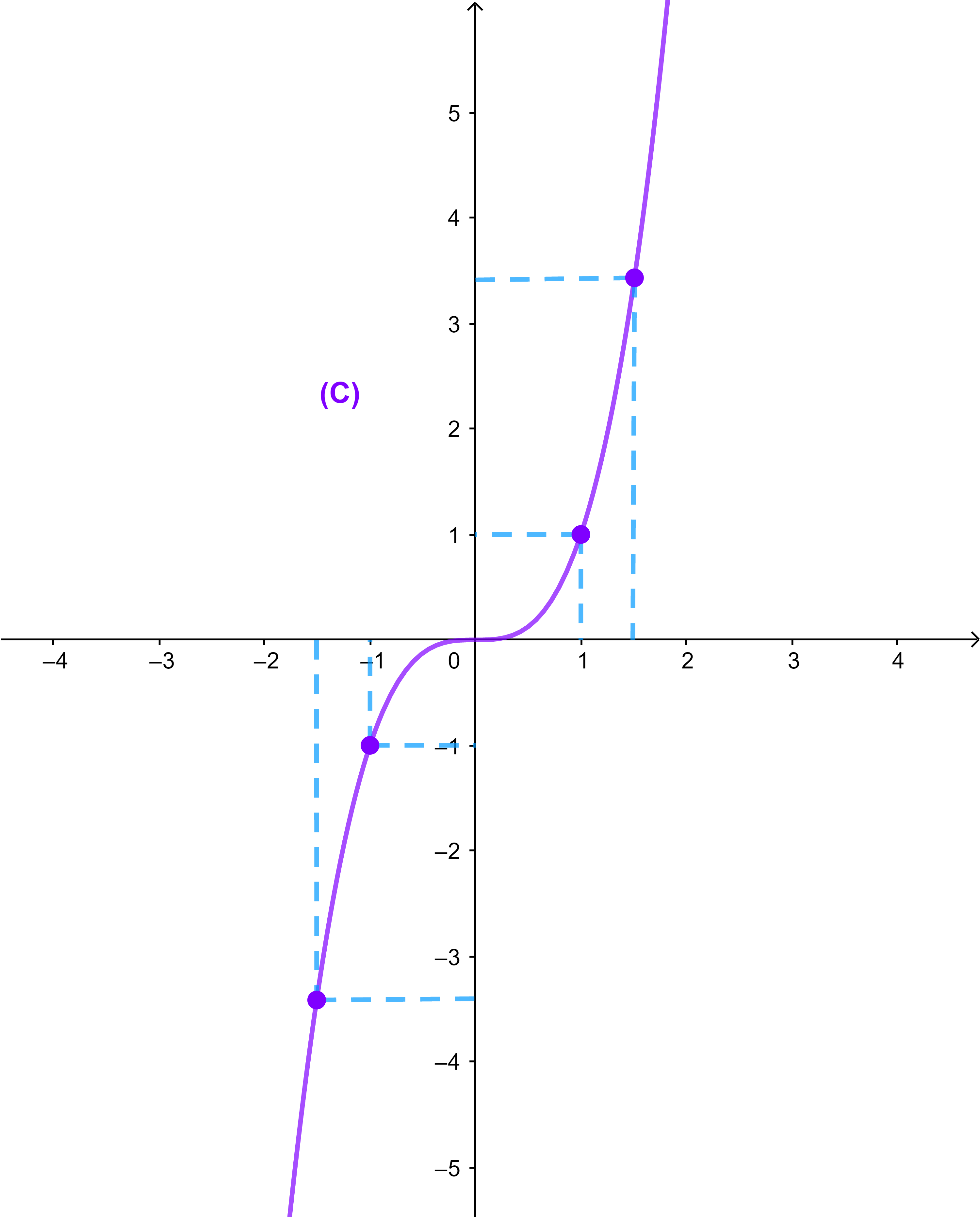
3.2.2 Exemple 1
Soit f une fonction définie par f(x)=x³ et (C) sa courbe représentative dans un repère orthonormé (O;i→;j→).
On a D=IR et a=1>0 donc f est strictement croissante sur IR.
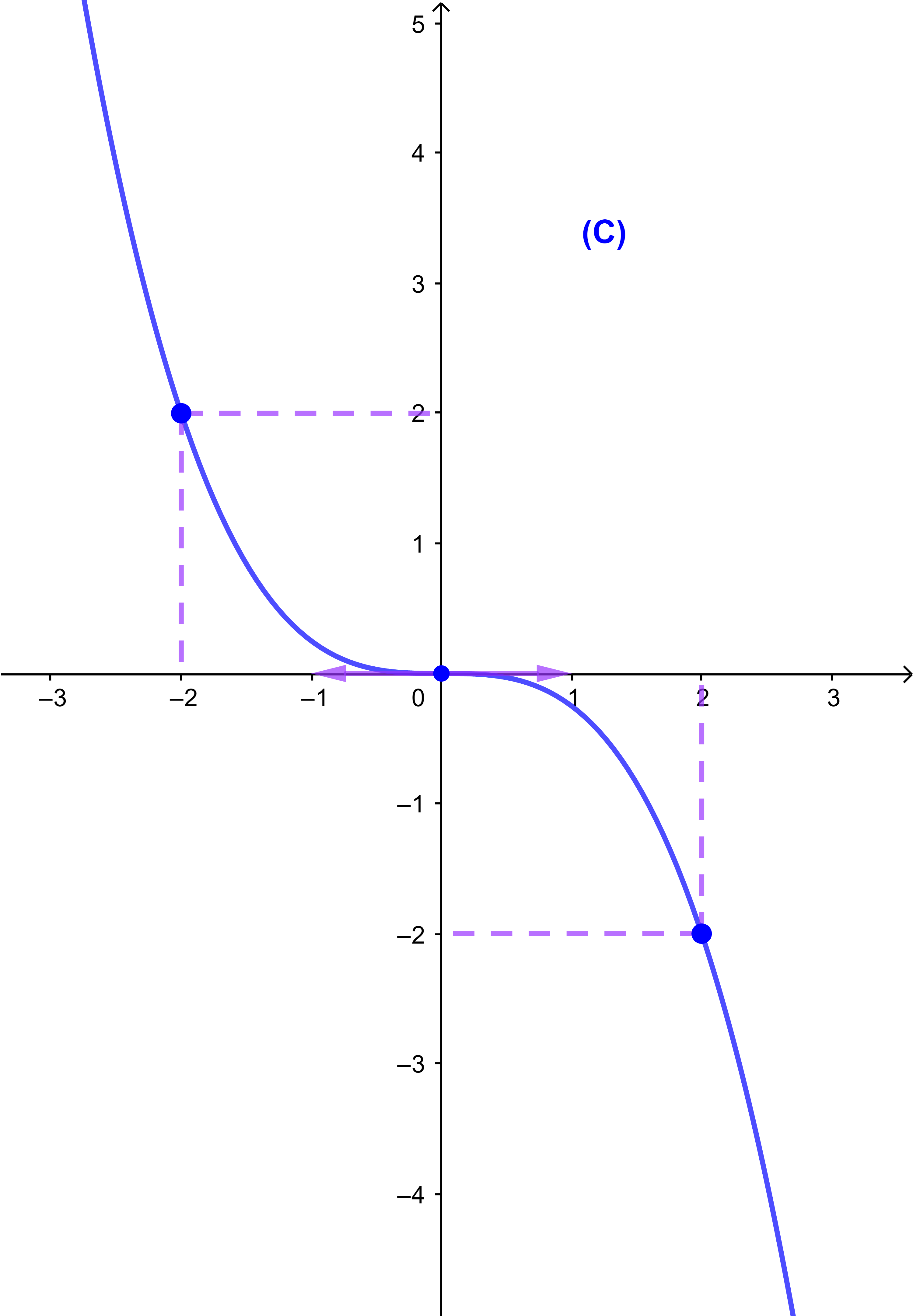
3.2.2 Exemple 2
Soit f une fonction définie par f(x)=-(0,25)x³ et (C) sa courbe représentative dans un repère orthonormé (O;i→;j→).
On a D=IR et a=-(0,25)<0 donc f est strictement décroissante sur IR.
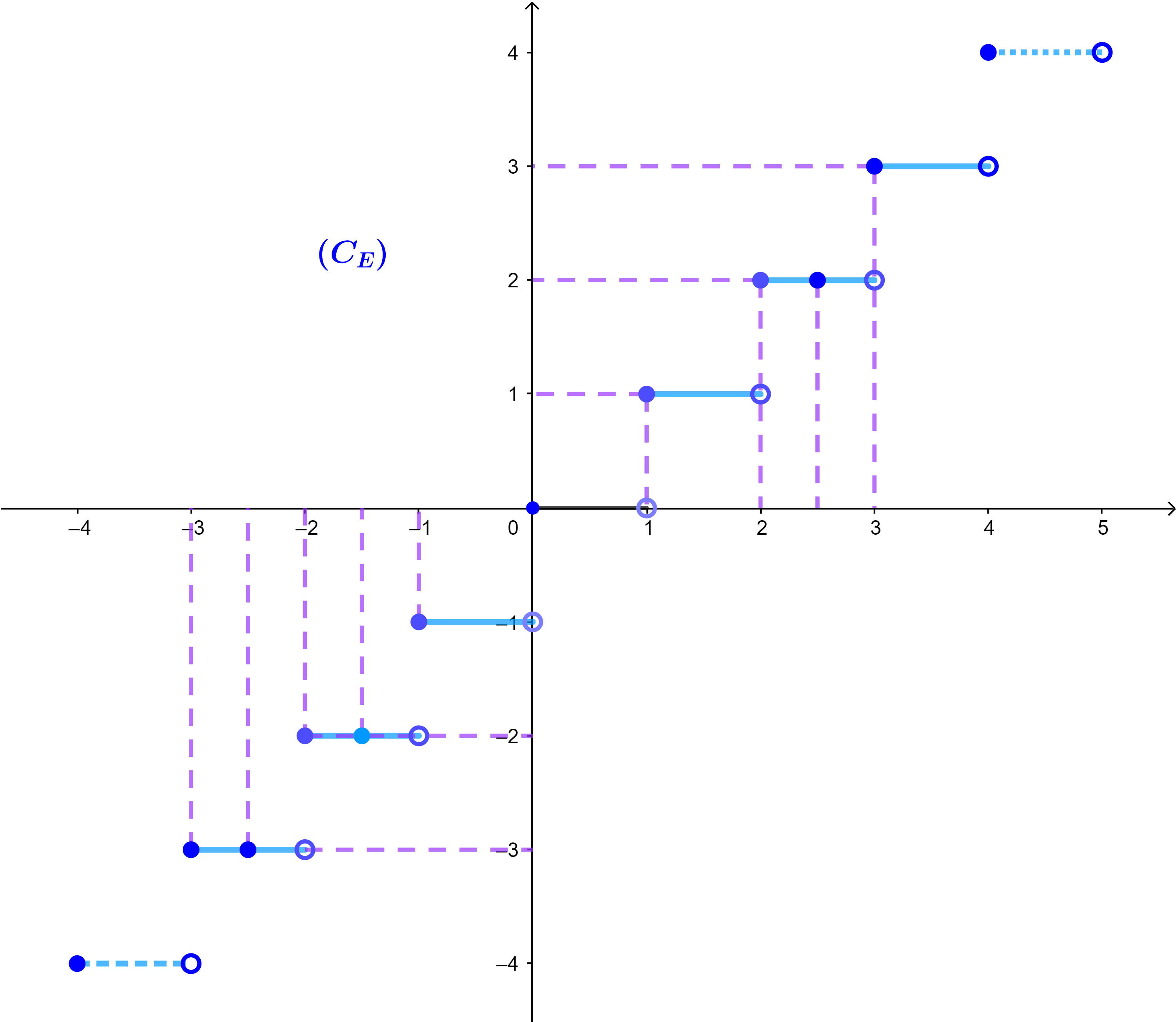
3.3 La fonction: x→E(x)
La fonction partie entière, notée E est définie sur des segments semi-ouverts à droite [i;i+1[ avec i∈ℤ
son domaine de définition est IR
(∀x∈IR)(∃!p∈ℤ): p≤x<p+1
E(x)=p ⇔ p≤x<p+1.
Exemples
Si x∈[-2;-1[ alors E(x)=-2.
Si x∈[3;4[ alors E(x)=3.