3- Représentation graphique

3.1 La fonction: x→√(x+a)

3.1.1 Propriété

Soient p une fonction de la forme p(x)=x+b avec b∈IR et f la fonction définie par f(x)=√(x+b).
f est définie et strictement croissante sur l'intervalle D=[-b;+∞[.

Démonstration
La fonction √ est strictement croissante sur IR⁺.
La fonction p: x→x+b est une fonction affine et a=1>0 donc elle est strictement croissante sur IR en particulier sur D.
∀x∈D on a (x+b≥0) donc p(D)⊂IR⁺
ainsi f=√op est strictement croissante sur D.

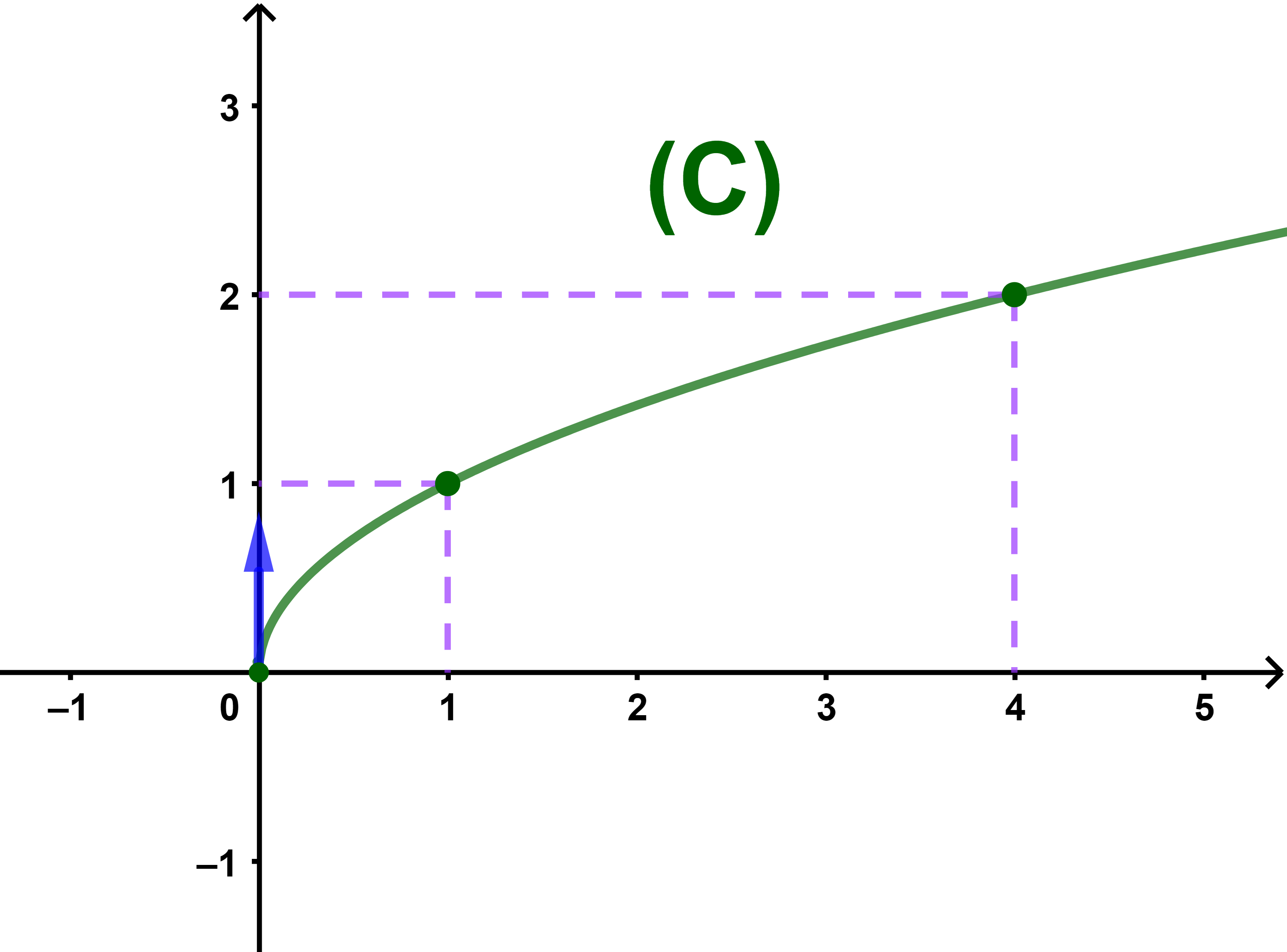
3.1.2 Exemple 1

Soit f une fonction définie par f(x)=√(x) et (C) sa courbe représentative dans un repère orthonormé (O;i^→;j^→).
On a D=[0;+∞[ et f est strictement croissante sur D.

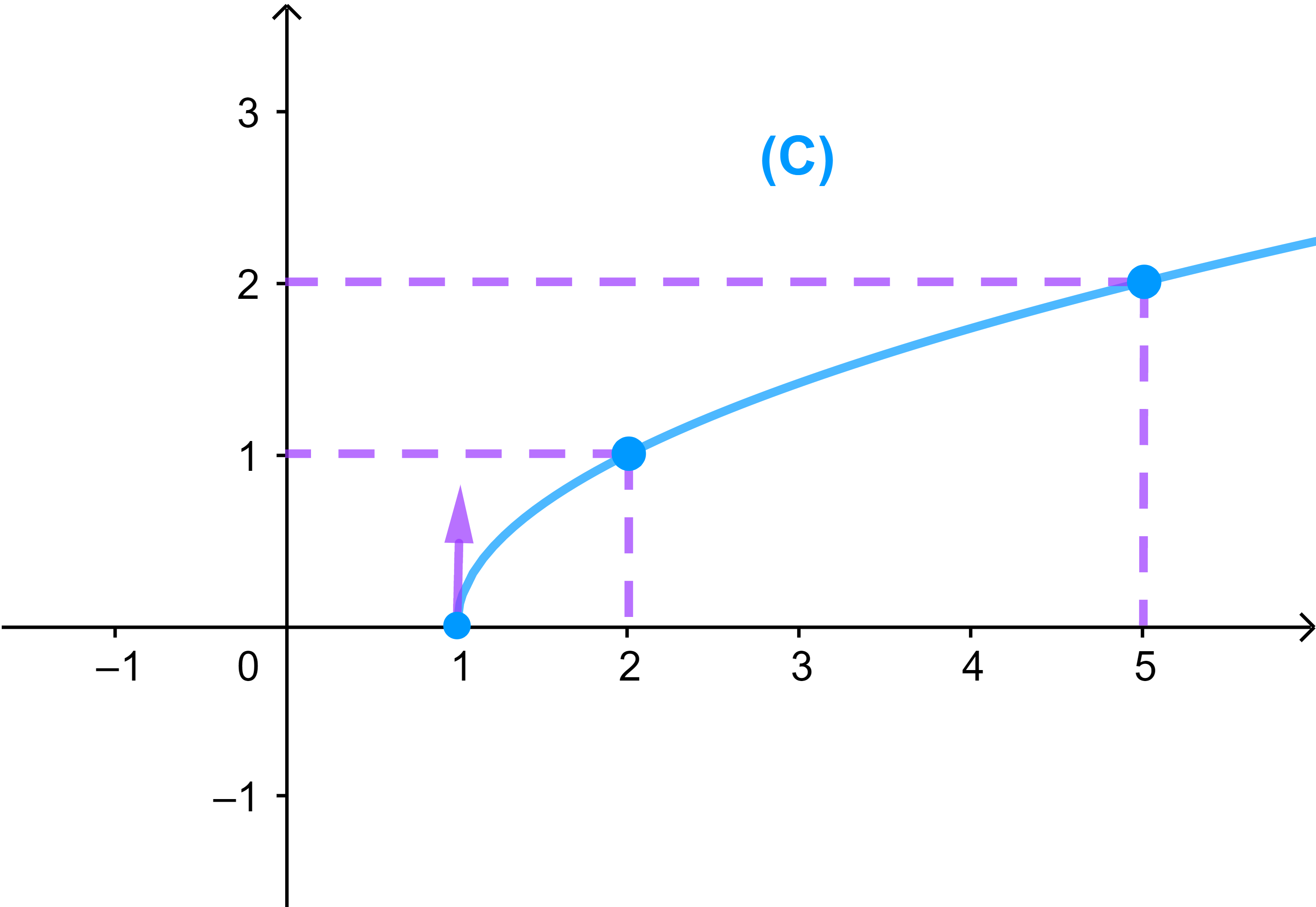
3.1.3 Exemple 2

Soit f une fonction définie par f(x)=√(x-1) et (C) sa courbe représentative dans un repère orthonormé (O;i^→;j^→).
On a D=[1;+∞[ et f est strictement croissante sur D.

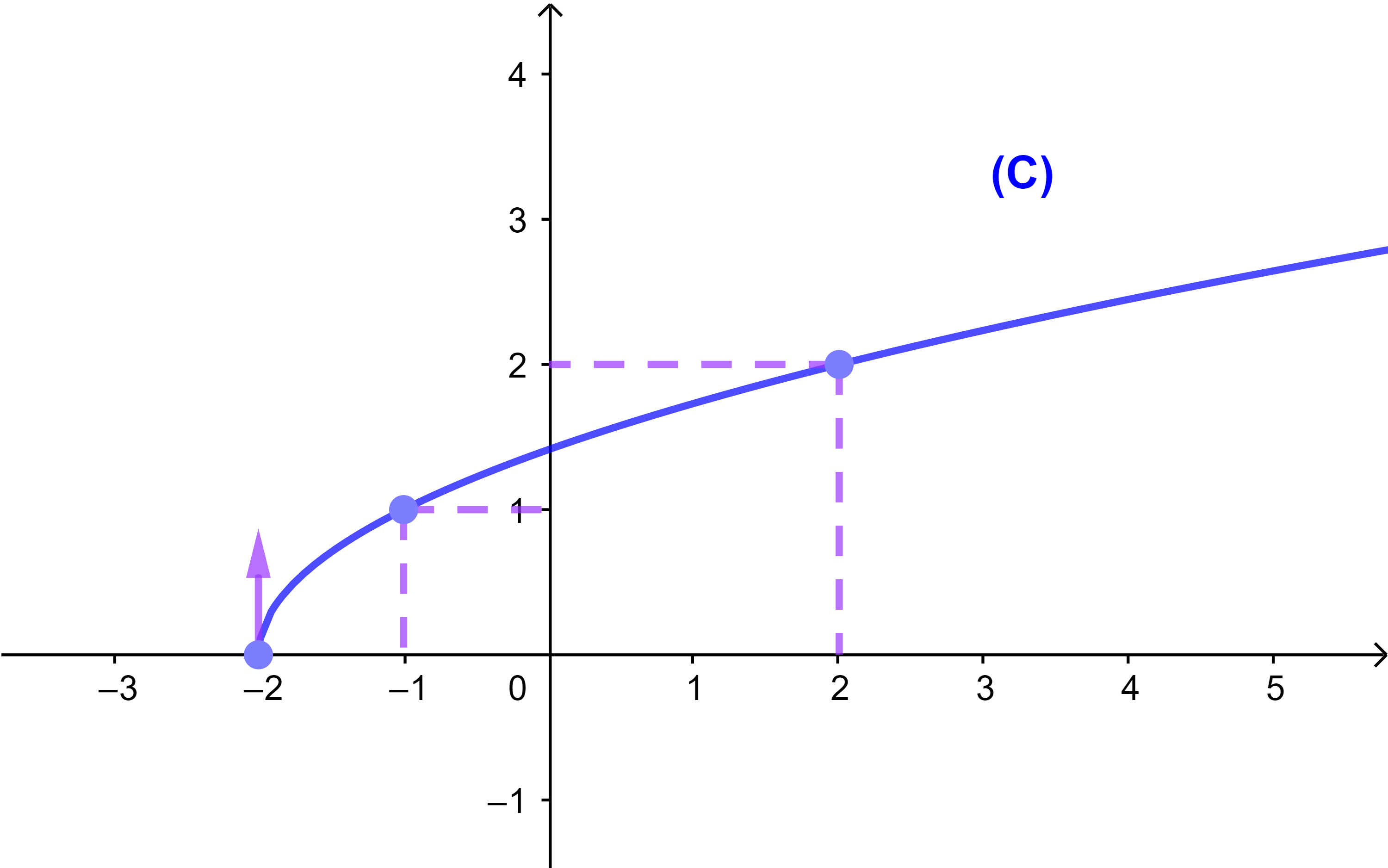
3.1.4 Exemple 3

Soit f une fonction définie par f(x)=√(x+2) et (C) sa courbe représentative dans un repère orthonormé (O;i^→;j^→).
On a D=[-2;+∞[ et f est strictement croissante sur D.