Généralités sur les fonctions (5)
Exercice 1 tp
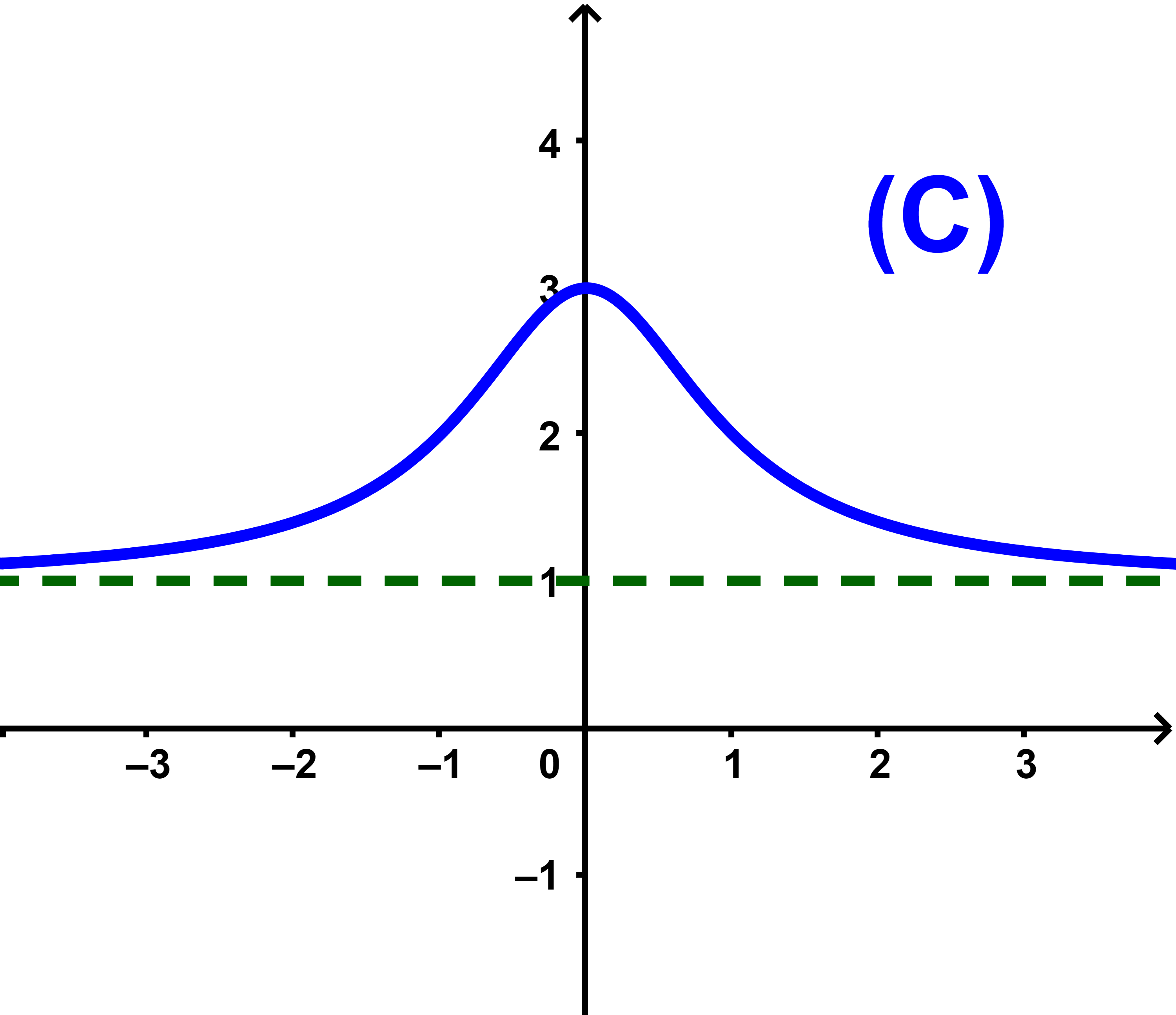
Soit f une fonction numérique définie par
| f(x) = 1+ | 2 |
| x²+1 |
1) Etudier la parité de f.
2) Montrer que (∀x∈IR): f(x)≤3.
3) Déduire que f admet un extremum.
Correction
1) (∀x∈IR): x²+1≠0
donc D=IR ainsi (∀x∈IR): -x∈IR.
Soit x∈IR
| f(-x) = 1+ | 2 | =1+ | 2 |
| (-x)²+1 | x²+1 |
∀x∈IR on a f(-x)=f(x) donc f est une fonction paire.
3) Montrons que (∀x∈IR): f(x)≤3.
Signe de f(x)-3
| f(x) - 3 = 1-3+ | 2 |
| x²+1 | |
| = -2+ | 2 |
| x²+1 |
| = | -2x²-2+2 |
| x²+1 | |
| = | -2x² |
| x²+1 |
on a x²+1>0 et -2x²≤0
donc (∀x∈IR): f(x)≤3.
4) On a f(x)≤3
il suffit de trouver a tel que f(a)=3.
On peut remarquer que f(0)=3
mais on le trouve en résolvant l'équation f(x)=3.
f(x)=3 ⇔ f(x)-3=0
| f(x) - 3 = 0 ⇔ | -2x² | = 0 |
| x²+1 |
⇔ -2x² = 0 (car x²+1≠0)
⇔ x=0
donc f(0)=3.
On a donc (∀x∈IR): f(x)≤f(0)
et cela signifie que f(0)=3 est une valeur maximale de f sur IR ainsi 3 est un extremum de f en 0.
1.5 Monotonie d'une fonction
1.5.1 Définitions
Soit f une fonction définie sur intervalle I.
1) f est croissante sur I si
(∀x;y ∈I): x<y ⇒ f(x)≤f(y).
2) f est strictement croissante sur I si
(∀x;y∈I): x<y ⇒ f(x)<f(y).
3) f est décroissante sur I si
(∀x;y∈I): x<y ⇒ f(x)≥f(y).
4) f est strictement décroissante sur I si
(∀x;y∈I): x<y ⇒ f(x)>f(y).
5) f est constante sur I si
(∀x;y∈I): x<y ⇒ f(x)=f(y).
Exemple 1
Soit f une fonction numérique définie par
f(x)=x³ étudier la monotonie de f sur IR.
Correction
f est un polynôme donc D=IR.
Soient x;y∈IR tels que x<y.
L'exposent 3 est impair donc l'inégalité ne chanche pas.
x<y ⇔ x³<y³ donc f(x)<f(y)
ainsi f est strictement croissante sur IR et donc f est strictement monotone sur IR.