Généralités sur les fonctions (6)
Exemple 2
Soit f une fonction numérique définie par f(x)=x²+2.
Etudier la monotonie de f sur IR+ et déduire sa monotonie sur IR-.
Correction
f est un polynôme donc D=IR.
1) Soient x;y∈IR+ tels que x<y.
x et y sont positifs donc l'inégalité ne change pas
x<y ⇔ x²<y² ⇔ x²+2<y²+2 ⇔ f(x)<f(y).
Ainsi f est strictement croissante sur IR+.
2) Notons que f est paire et de plus croissante sur IR+ alors f est strictement décroissante sur IR- et par conséquent f n'est pas une fonction monotone sur IR.
| x | -∞ | 0 | +∞ | |||
| f | ↗ |
2 | ↘ |
1.5.2 Interprétation géométrique
Soit f une fonction numérique et (C) sa courbe représentative dans un repère.
1) f est strictement croissante sur ]-∞;x0].
2) f est constante sur [x0;x1].
3) f est strictement décroissante sur [x1;+∞[.
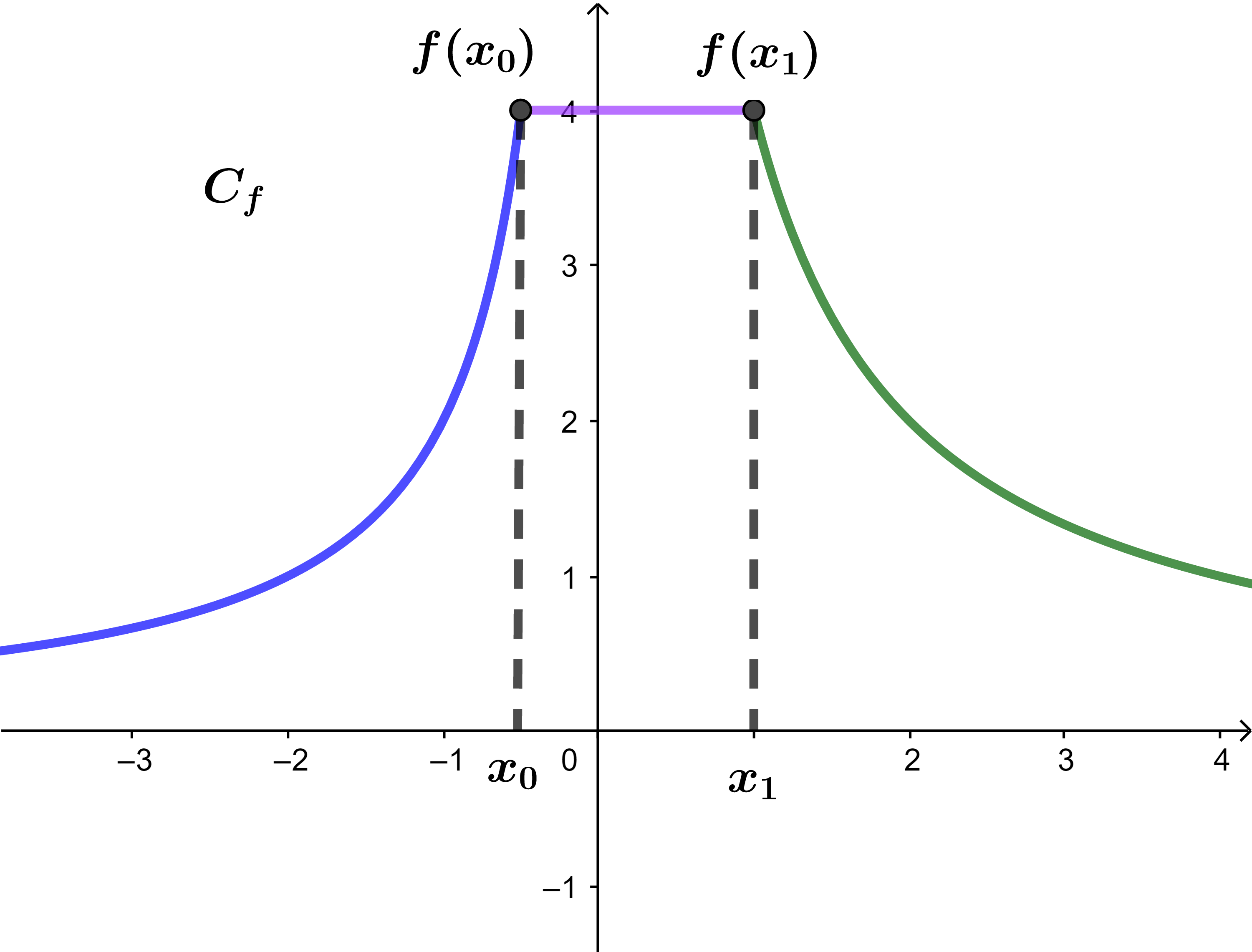
Tableau de variations de f
| x | -∞ | x0 | x1 | +∞ | |||
| f | ↗ | ---- | ↘ |
1.5.3 Taux d'accroissement
Définition et propriétés
Soient f une fonction numérique définie sur un intervalle I et x;y∈I.
| T(x;y) = | f(x)-f(y) | (x≠y) |
| x-y |
est le taux d'accroissement de f entre x et y.
(a) f est croissante sur I
⇔ (∀x;y∈I tels que x≠y): T(x;y)≥0.
(b) f est décroissante sur I
⇔ (∀x;y∈I tels que x≠y): T(x;y)≤0.
Exercice 1 tp
Soit f une fonction numérique définie par
f(x)= -x²+4x.
Etudier la monotonie de f
sur ]-∞;2] puis sur
[2;+∞[.
Correction
f est un polynôme donc D=IR.
Soient x;y∈IR tels que x≠y.
f(x)-f(y)=-x²+4x-(-y²+4y)=-(x²-y²)+4(x-y)
=-(x-y)(x+y)+4(x-y)=-(x-y)(x+y-4)
donc T(x;y)=-(x+y-4) est le taux d'accroissement de f entre x et y.
1) (a) Si x;y∈]-∞;2] alors x≤2 et y≤2.
Puisque (x≠y) alors
x+y<4.
x+y-4<0 ⇔ -(x+y-4)>0 ⇔ T(x;y)>0
ainsi f est strictement croissante
sur ]-∞;2].
(b) Si x;y∈[-2;+∞[ alors x≥2 et y≥2.
Puisque (x≠y) alors x+y>4.
x+y-4>0 ⇔ -(x+y-4)<0 ⇔ T(x;y)>0
ainsi f est strictement décroissante sur [2;+∞[.
2) Tableau de variations de f
| x | -∞ | 2 | +∞ | |||
| f | ↘ | 4 |
↗ |
Exercice 2 tp
Soit f une fonction définie sur I=[-3;3] par f(x)=x³-12x.
1) Etudier les variations de f sur chacun des intervalles suivants
[-3;-2] ; [-2;2] et [2;3].
2) Tracer le tableau de variations de f sur I.
2) Déduire des extremums de f sur I.