Produit scalaire (8)
3.4 Positions relatives d’un cercle et une droite
3.4.1 Propriété
Soient (D) une droite et (C) un cercle
de centre Ω et de rayon R.
Il y'a trois cas positions.
Si d(Ω;(D)) > R
alors (D) ne coupe pas (C).
Dans ce cas (D)∩(C)=∅.
(D)
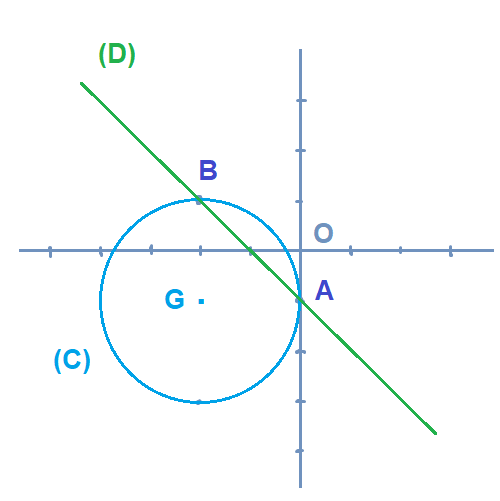
Si d(Ω;(D)) < R
alors (D) coupe (C) en deux points A et B.
Si d(Ω;(D)) = R
alors (D) coupe (C) en un seul point
dans ce cas (D) est tangente
au cercle (C).

3.4.2 Equation de la tangente au cercle
Le plan ℙ est rapporté à un repère orthonormé (O;i→;j→). On considère dans ℙ un cercle (C) de centre Ω
et d'équation
x²+y²+ax+by+c=0 et une droite (D) tangente au cercle (C) au point A.
| Ω( | -a | ; | -b | ) et R=√( | a²+b²-4c | ) |
| 2 | 2 | 4 |
M(x;y)∈(D) ⇔ AM→.ΩM→=0
| ⇔ (x-xA)(x+ | a | )+(y-yA)(y+ | b | )=0 |
| 2 | 2 |
Propriété
Le plan ℙ est rapporté à un repère orthonormé (O;i→;j→).
On considère dans ℙ un cercle (C) d'équation cartésienne
x²+y²+ax+by+c=0 et A(xA;yA)∈(C).
L'équation de la tangente du cercle (C) au point A est définie comme suit
| (x-xA)(x+ | a | )+(y-yA)(y+ | b | )=0 |
| 2 | 2 |
Exercice 1 tp
Le plan ℙ est rapporté à un repère orthonormé (O;i→;j→).
On considère dans ℙ un cercle (C) de centre
Ω(-2;1) et de rayon R=3.
Déterminer la tangente au cercle (C) au point A(-2;4).