2.2 Conservation de la mesure d’un angle orienté

2.2.1 Propriété

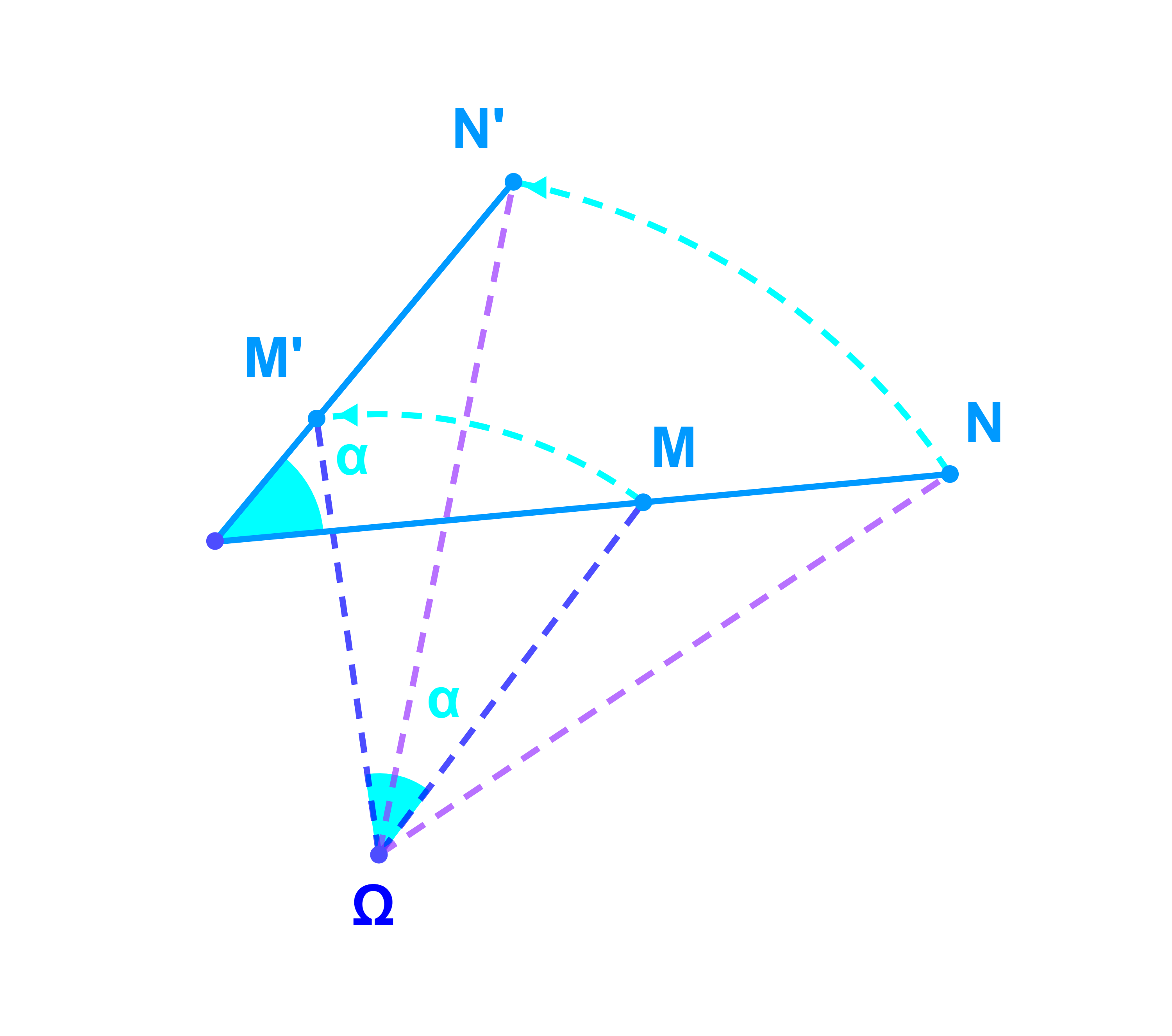
Soient R(Ω ; α) une rotation et M et N deux points.
Si R(M)=M' et R(N)=N' alors (MN;N'N')≡α[2π].

2.2.2 Propriété

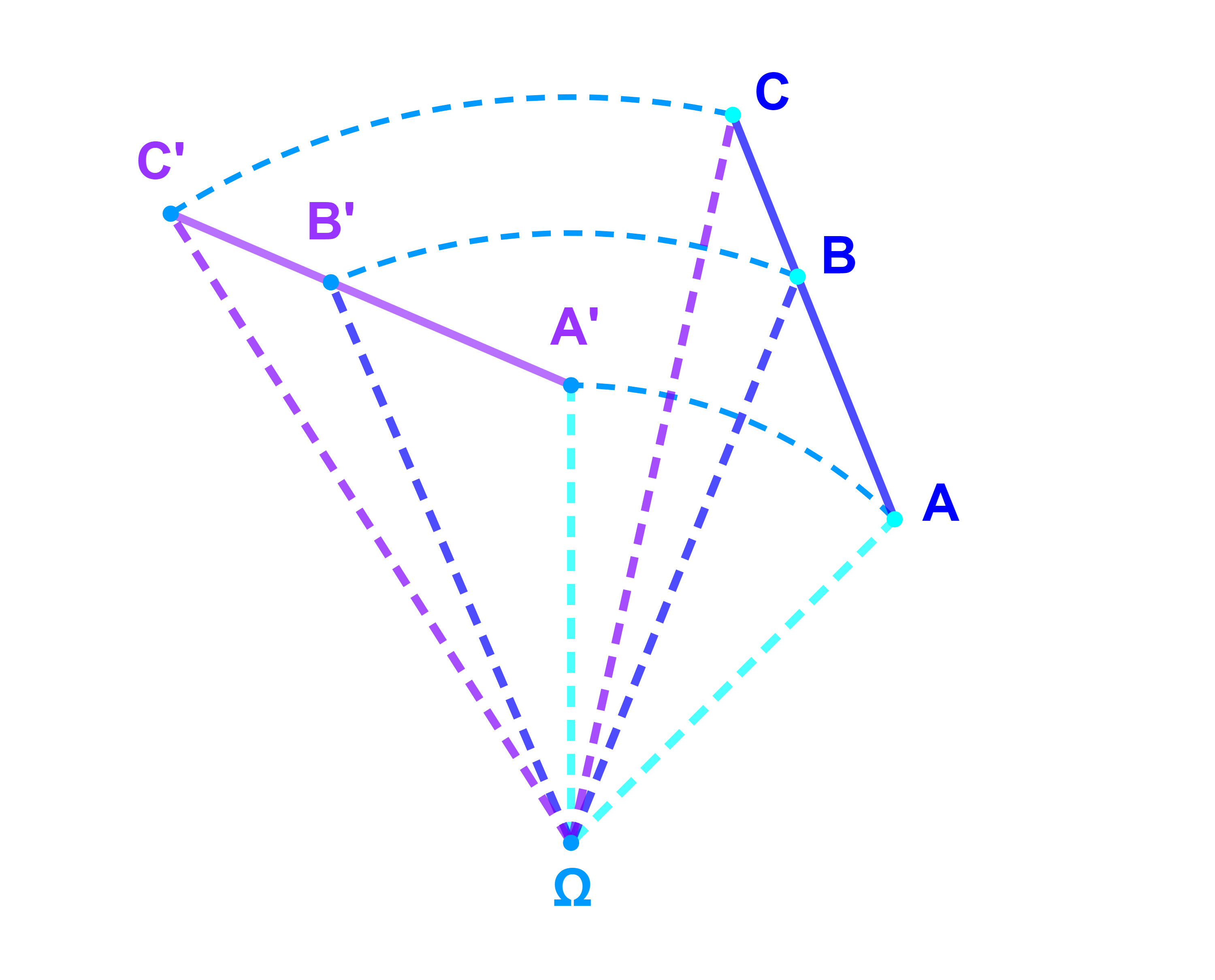
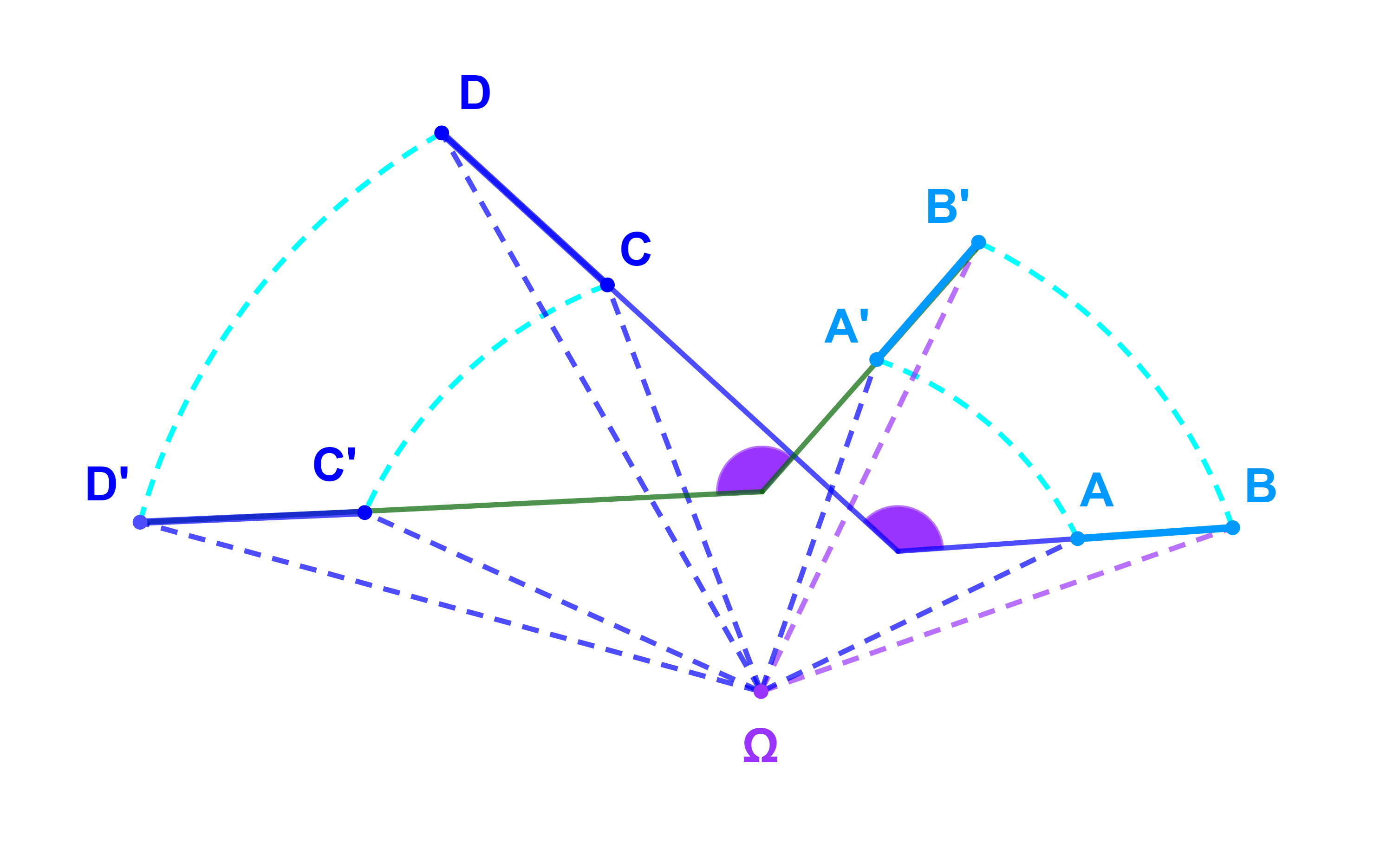
Soient R une rotation et A;B;C;D quatre points tels que A≠B et C≠D.
Si R(A)=A'; R(B)=B'; R(C)=C' et R(D)=D'
alors (AB ; CD)≡(A'B';C'D')[2π].

Résultat
La rotation conserve la mesure des angles orientés.

2.3 Conservation du barycentre

2.3.1 Propriété

Soient R une rotation et G le barycentre de deux points pondérés (A;a) et (B;b).
Si A' ; B' et G' sont les images réspectives de A ; B et G par R alors G' est le barycentre de (A';a) et (B';b).

Résultat
1) La rotation conserve le barycentre (de deux points ou trois points ou quatre ..).
2) la rotation conserve le milieu d'un segment.

2.3.2 Propriété de la coliéarité

Soient R une rotation et A' ; B' ; C' respectifs les images des points A ; B et C par R.
Si AC^→=k(AB^→) tel que (k∈IR)
alors A'C'^→=k(A'B'^→).

Résultats
1) La rotation conserve le coefficient de coliéarité de deux vecteurs.
2) La rotation conserve l'alignement des points.