La rotation dans le plan (3)
3- L’image par une rotation
3.1 L’image d’une droite et d'un segment
3.1.1 Propriété
Soient R une rotation et A ; B deux points.
Si A' et B' sont des images respectivement de A et B alors R(AB)=(A'B').
En d'autre terme
R(A)=A' et R(B)=B' ⇒ R(AB)=(A'B').
Résultat
1) L’image d’une droite par une rotation est une droite.
2) L'image d'une demi-droite par une rotation est une demi-droite.
3.1.2 Propriété
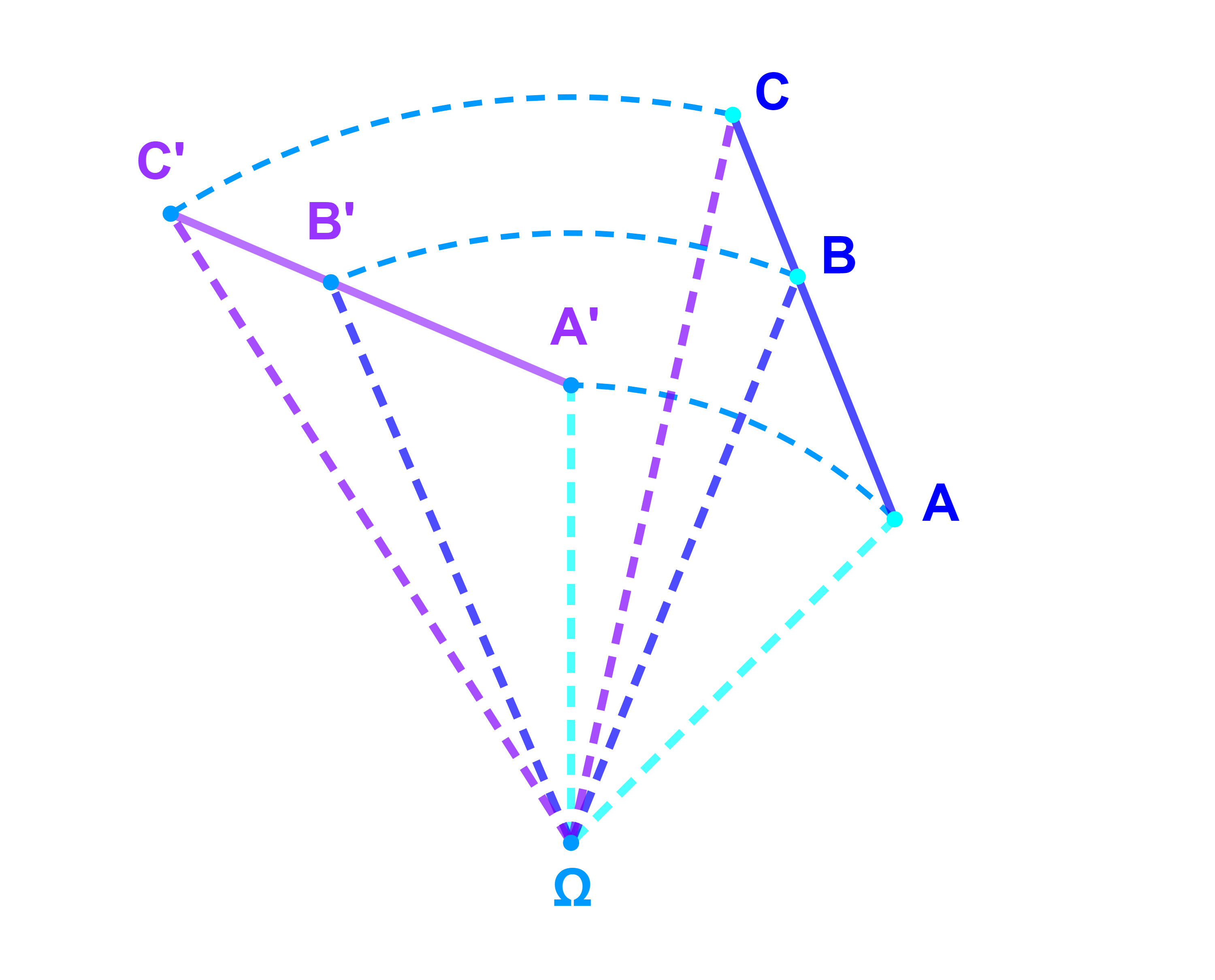
L’image d’un segment [AB] par une rotation R est un segment [A'B'].
En d'autre terme
R(A)=A' et R(B)=B' ⇒ R([AB])=[A'B'].
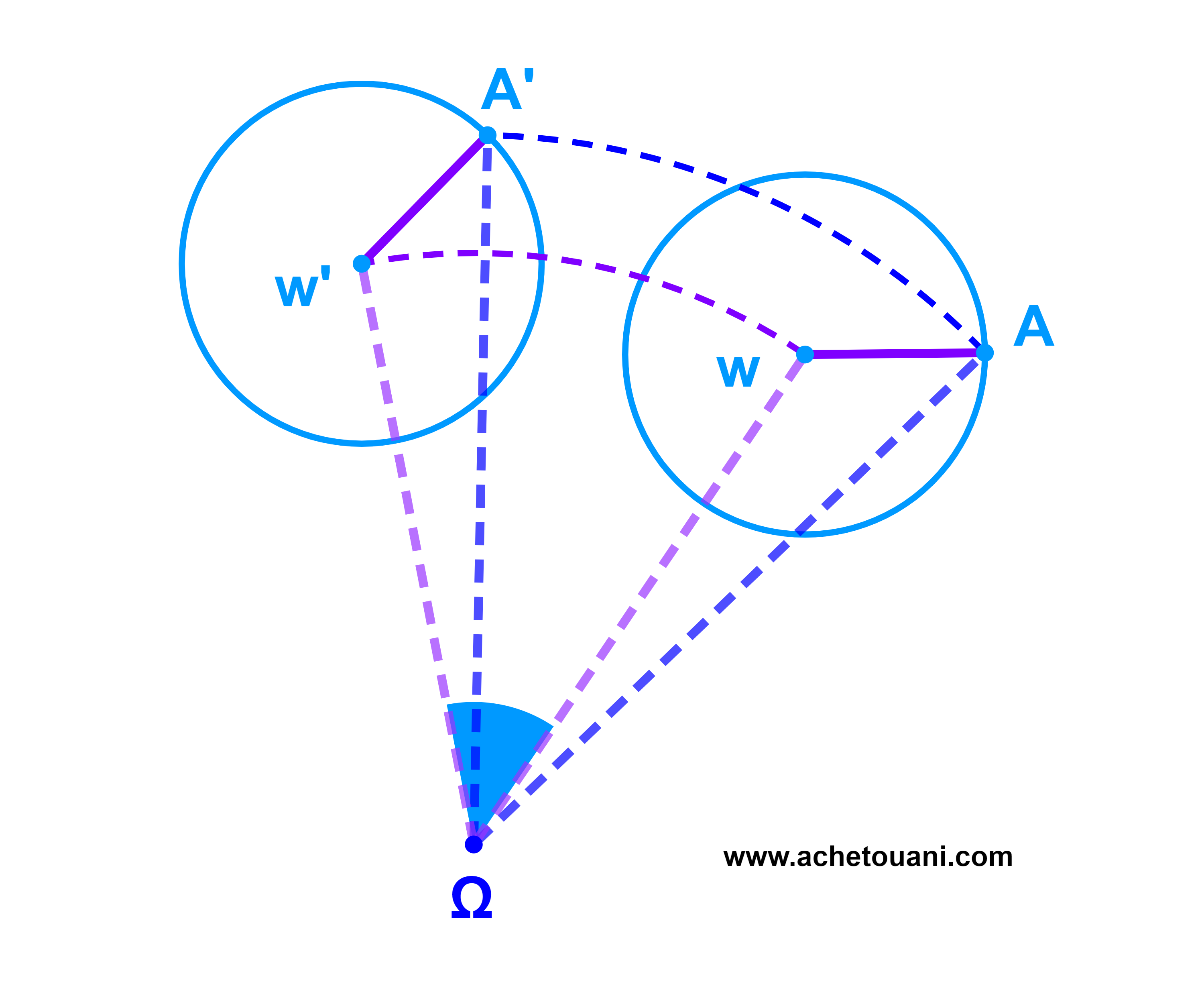
3.2 L’image d’un cercle
L’image d’un cercle C(O;r) de centre O et de rayon r par une rotation R est un cercle C(O';r) de même rayon r et de centre O'= R(O).
3.4 Conclusions
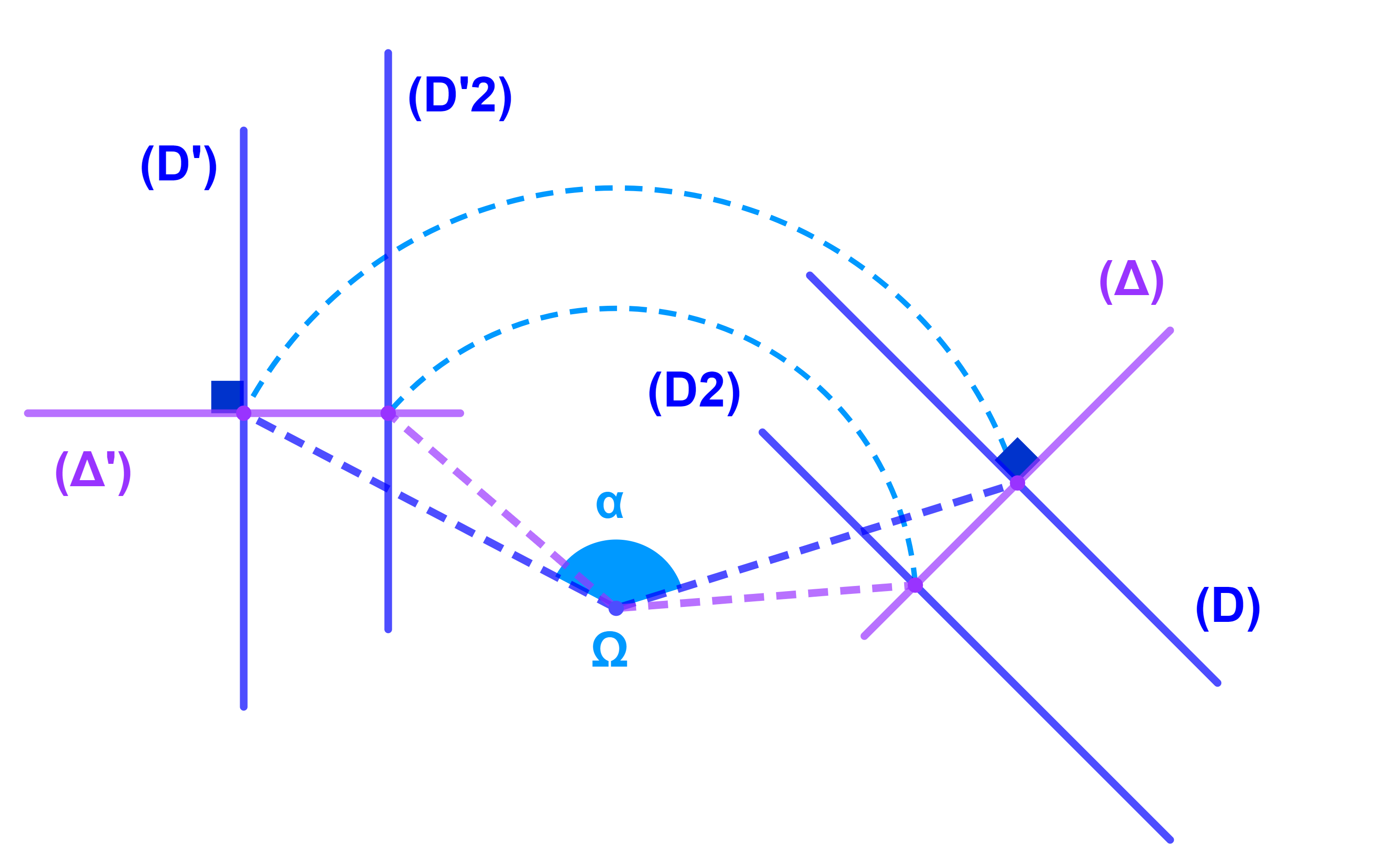
1) Soient R une rotation. On considère deux droites (D1) et (D2)
On pose R(D)=(D') et R(Δ)=Δ'.
(a) Conservation de l’orthogonalité
Si (D)⊥(Δ) alors (D')⊥(Δ').
(b) Conservation du parallèlisme
Si (D)||(Δ) alors (D')||(Δ').
(c) Si A∈(D)∩(Δ) alors R(A)=A'∈(D')∩(Δ').