La rotation dans le plan (4)
4- Décomposition d’une rotation et Composée de deux rotations
4.1 Décomposition d’une rotation
4.1.1 Construction
Soient R(Ω;α) une rotation ; (D) et (D') deux droites passant par Ω et forment un angle
de mesure ((D);(D'))=θ+kπ (k∈ℤ).
On considère S et S' deux symétries axiales
d'axes respectives (D) et (D').
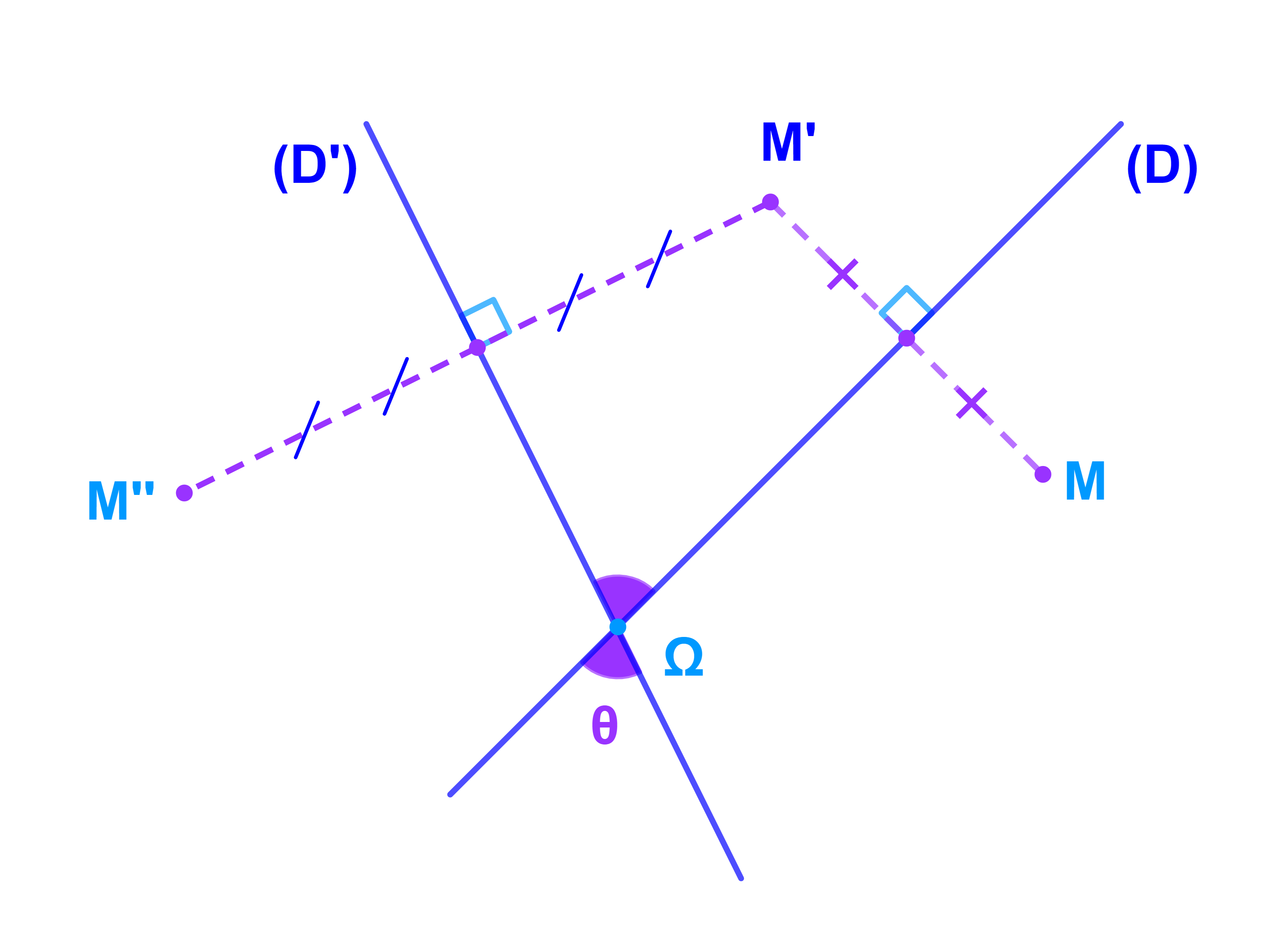
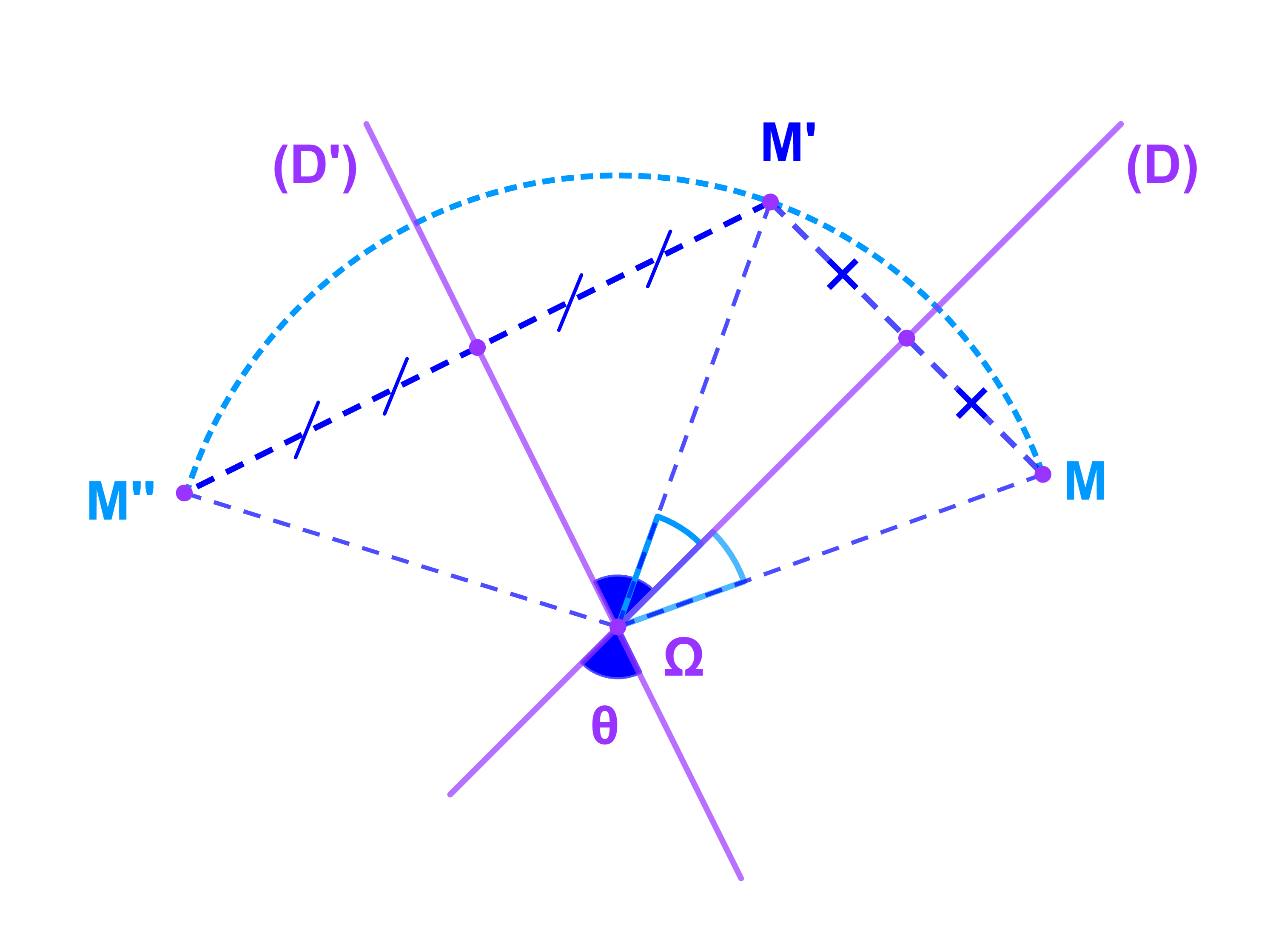
Soit M un point du plan.
On pose S(M)=M' et S'(M')=M" donc S'oS(M)=M".
S(M)=M' ⇔ ((D) est médiatrice du segment [MM'])
donc ΩM=ΩM'.
S'(M')=M" ⇔ (D') est médiatrice du segment [M'M"]
donc ΩM'=ΩM"
ainsi ΩM=ΩM'=ΩM".
On a
(ΩM;ΩM")=(ΩM;ΩM')+(ΩM';ΩΩM")+ 2kπ
= 2(ΩE;ΩM')+2(ΩM';ΩF)+2kπ (voir figure)
=2(ΩE;ΩF) + 2kπ
et donc ΩM=ΩM" et (ΩM;ΩM")=2θ+2kπ
cela signifie que
S'oS est une rotation de centre Ω et d'angle 2θ.
r=SoS' ⇔ 2θ= α
il suffit donc de prendre
| θ=( | α | )+2kπ |
|---|---|---|
| 2 |
4.1.2 Propriété 1
Soient D(Ω;u) ; D'(Ω;u') deux droites sécantes ; S et S'
deux symétries axiales d'axes respectives (D) et (D').
S'oS est une rotation de centre Ω et d'angle
2(u→ ; u'→).
4.1.3 Propriété 2
Une rotation est une composée de deux symétries axiales sécantes au centre de la rotation.
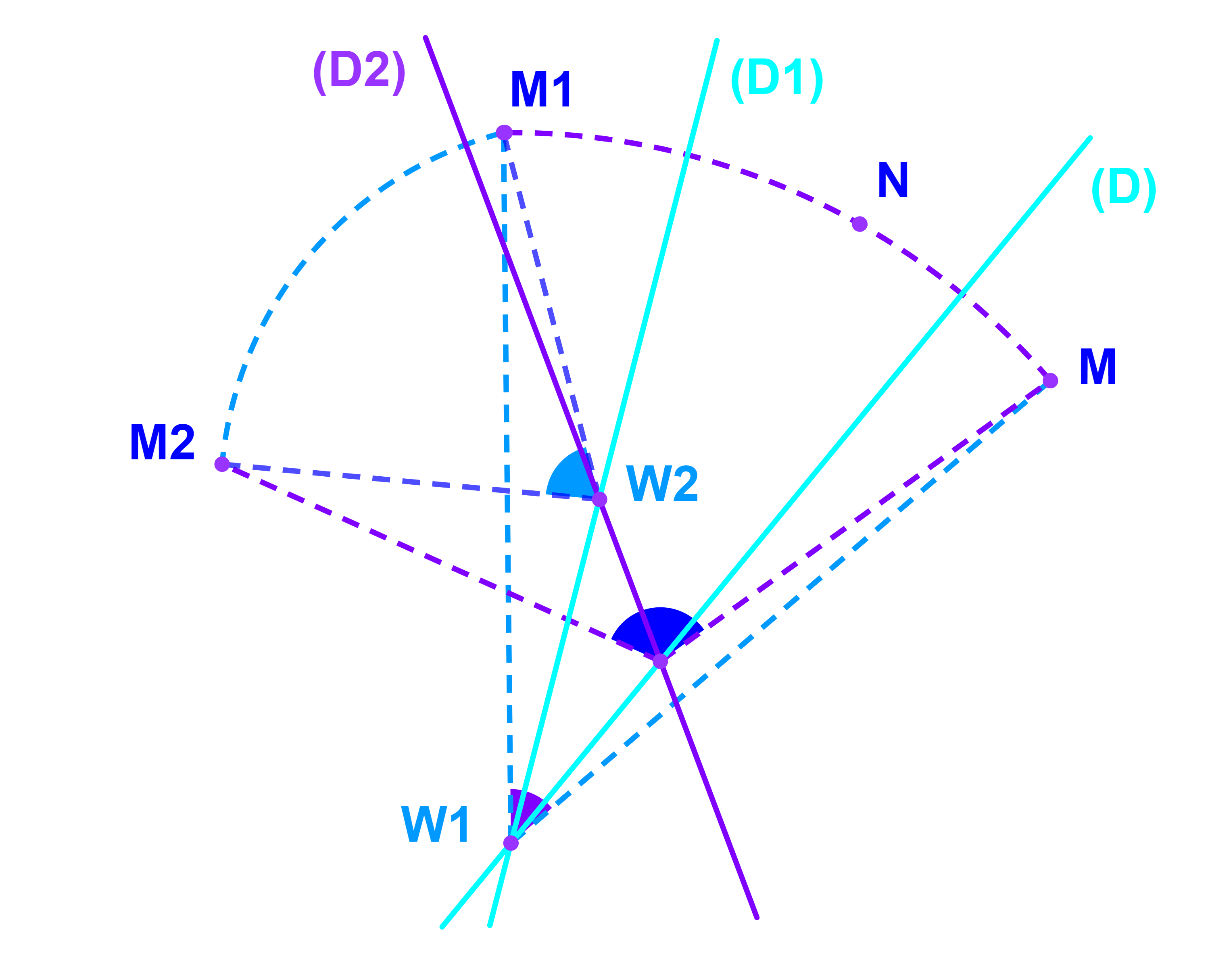
4.2 Composée de deux rotations
4.2.1 Construction
Soient r(W;α) et r(W';α') deux rotations
donc chacune est la composée de deux symétries axiales.
On pose r1 = S1D1oSD et r2 = S2D2oS1D1
donc r2or1 = S2D2oS1D1oS1D1oSD.
| { | (D;D1) = | α1 | + kπ et W1∈D∩D1 |
| 2 | |||
| (D1;D2) = | α2 | + kπ et W2∈D1∩D2 | |
| 2 |
or W1≠W2 donc (D1)=(W1W2)
ainsi r2or1 = S2D2oSD.
| (D;D2) = | α1+α2 | + kπ avec α+α'≠2π |
| 2 |
4.2.2 Propriété
La composée de deux rotations r1=(W1;α1) et r2(W2;α2) avec (α1+α2≠2π) est une rotation d'anlge α1+α2.