Exercice 1 tp

Soient EAB ; ECD deux triangles isocèles et rectangles en E.

1) Déterminer une rotation qui transforme A en B et C en D.

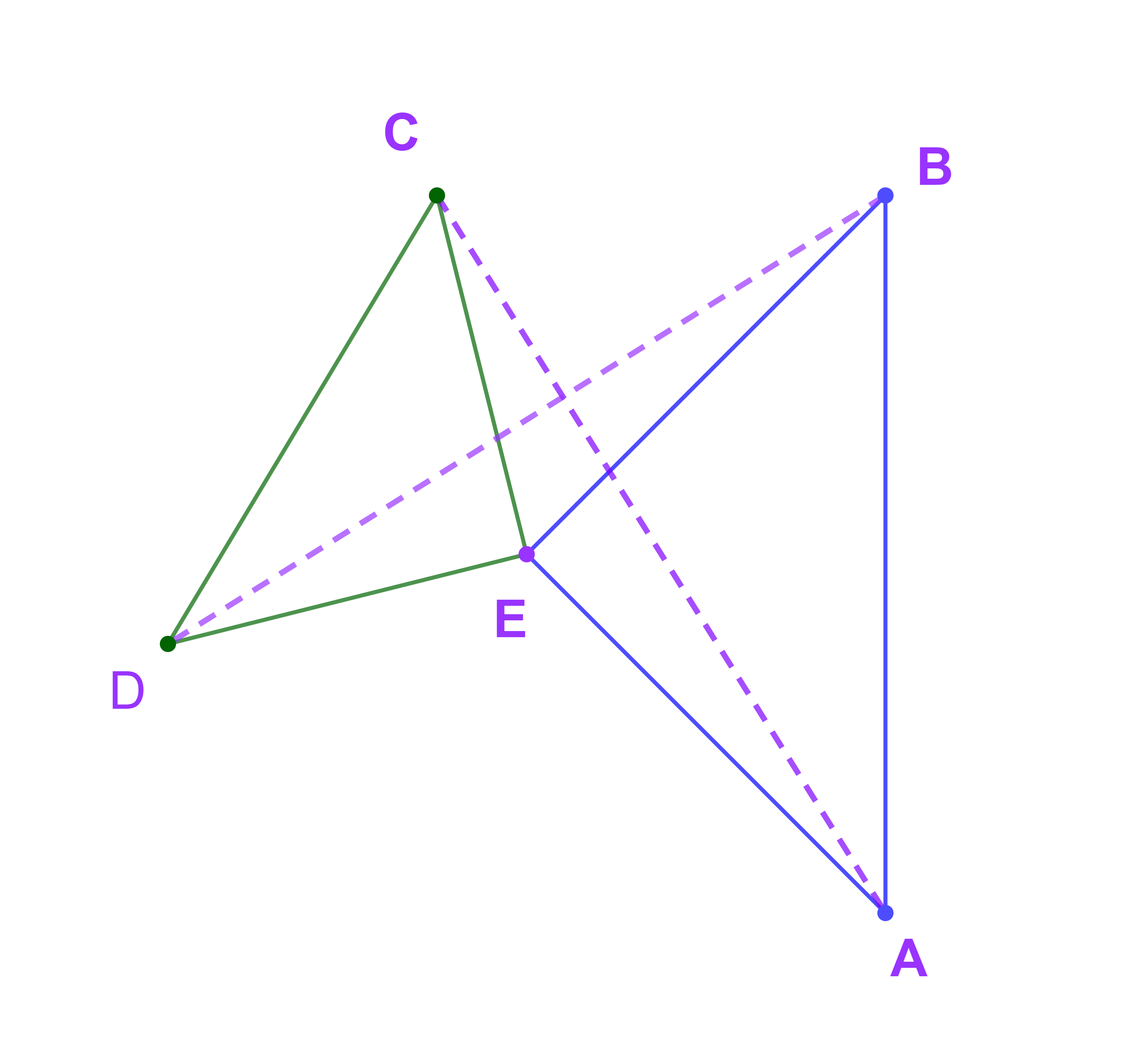
2) Montrer que AC=BD.
3) Déterminer la position relative de (AC) et (BD).

Exercice 2 tp

Soit ABC un triangle isocèle et rectangle en A.

(CA;CB)≡	π	[2π]
	4

1) Tracer la figure.
2) Déterminer le centre et le rayon de la rotation R qui transforme C en B et I en A tel que C est le milieu du segment [AI].

Correction

1)

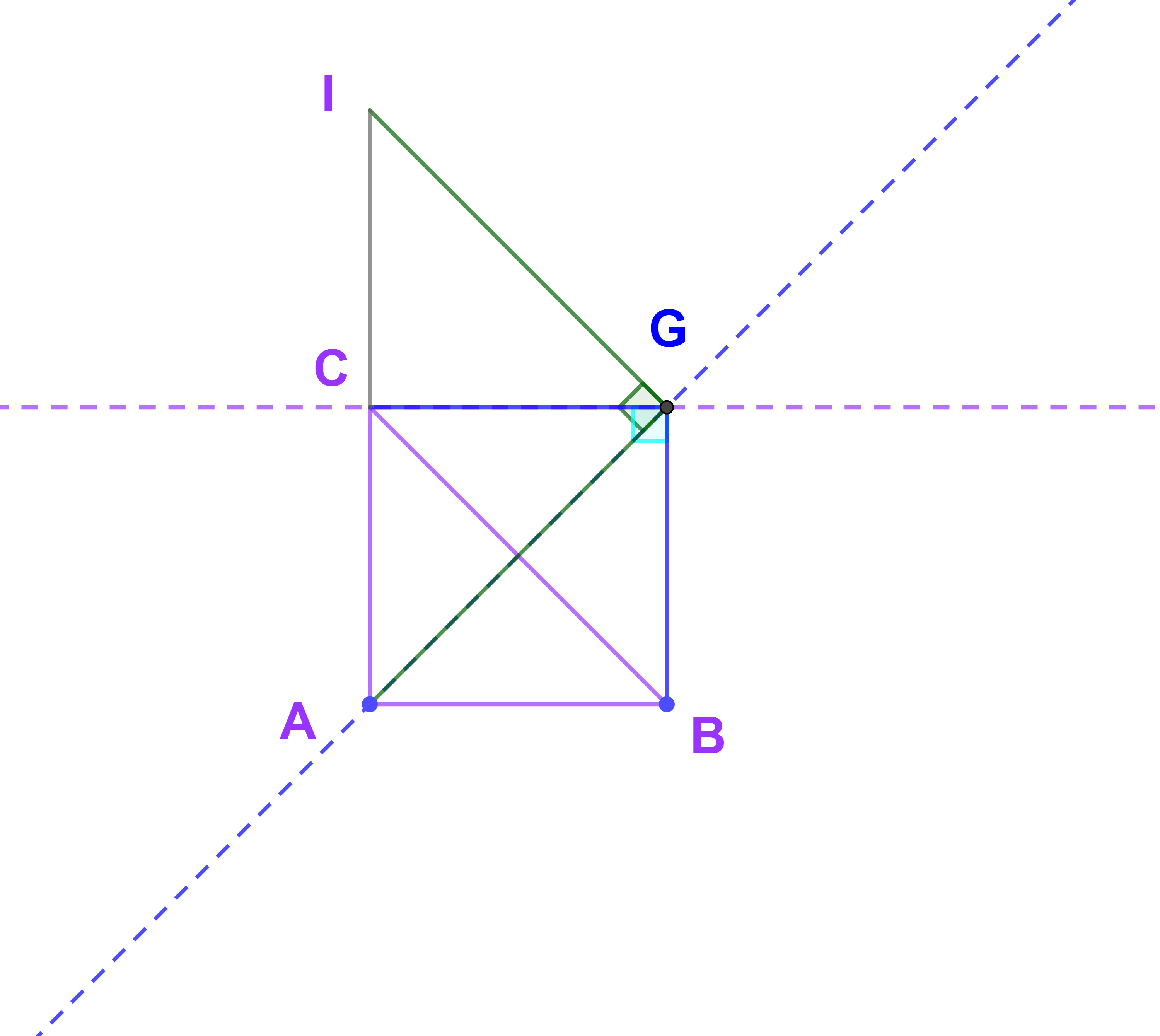
2) On désigne par G au centre de la rotation r.
R(B)=C ⇒ G∈med(BC)
R(A)=I ⇒ G∈med(AI)
donc med(BC)∩med(AI)={G}.
On a aussi med(BC)=(AG) car ABC est un triangle isocèle et de plus rectangle en A donc

(AG;AC)≡	π	[2π]
	4

Ainsi

(GC;GA)≡	π	[2π]
	4

et donc l'angle de la rotation R est

α ≡	π	[2π]
	2