Exercice 1 tp

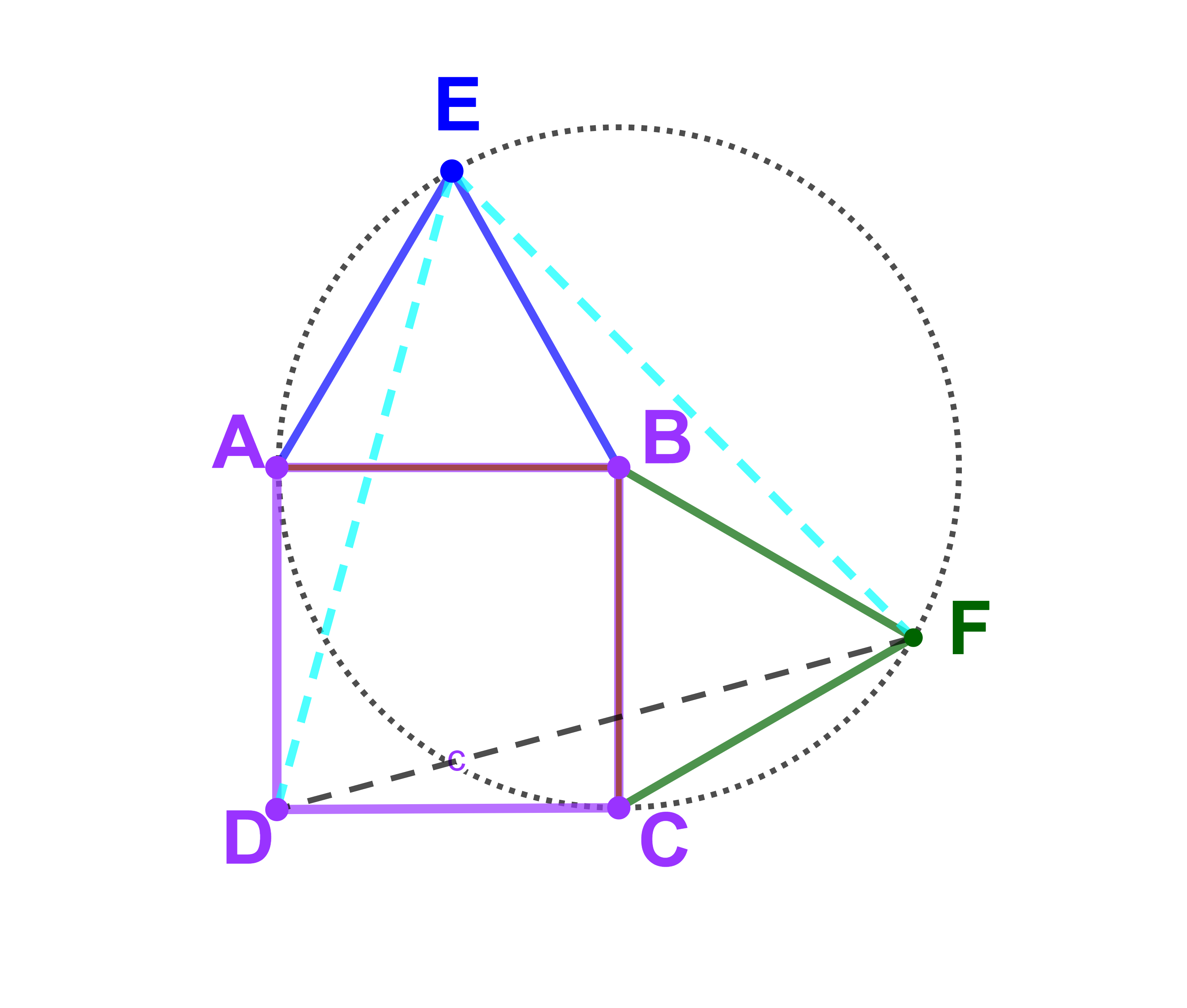
Soient ABCD un carré , E ; F deux points à l'extérieur du carré et EAB ; FBC deux triangles équilatéraux.
On considère que l'angle (EA;EB) est orienté positivement.
1) Tracer la figure.

2) Soit R une rotation de centre E

et d'angle	π
	3

(a) Vérifier que R(A)=B.
(b) Montrer que R(D)=F.
3) Quelle est la nature du triangle EDF ?

Correction

1)

2) (a) EAB est un triangle équilatèral

donc {	(EA;EB)≡	π	[2π]
		3
	EA=EB

et cela signifie que R(A)=B.

(b) On montre que R(D)=F
le triangle AED est isocèle de sommet A car AE=AD
et on a BEF isocèle de sommet B car BE=BF.
Pour montrer que ED=EF il suffit de montrer que les deux angles [EAD] et [EBF] ont la même mesure.

(AD;AE)≡	π	+	π	≡	5π
	2		3		6

On a

(BF;BE)≡2π -	π	-	2π	≡	5π
	2		3		6

Donc (BF;BE)≡(EA;ED)[2π] ou encore

{	(ED;EF)≡	π	[2π]
		3
	ED=EF

ainsi R(D)=F.

3) Le triangle EDF est équilatèral

car ED=EF et (ED;EF)=	π
	3