(1) الاعداد العقدية
1- المجموعة ℂ
تقديم
المعادلة x+1=0 ليس لها حل في IN لكن لها حل في ℤ
المعادلة 2x+1=0 ليس لها حل في ℤ لكن لها حل في ℚ
المعادلة x²-2=0 ليس لها حل في Q لكن لها حلين في IR
المعادلة x²+1=0 ليس لها حل في IR لان مربع عدد حقيقي موجب
عالم ايطالي تخيل عددا مربعه سالب, هذا العدد رمزله من بعده بالرمز i من L.Euler عام 1777 و i²=-1
i هو عدد خيالي لا ينتمي الى المجموعة IR
وبواسطة هذا العدد الجديد كونت الاعداد العقدية التي تكتب على الشكل
a+ib حيث a;b∈IR و i²=-1.
مجموعة الاعداد العقدية رمز لها بالحرف ℂ.
1.1 مبرهنة وتعاريف
1.1.1 مبرهنة 1 (مقبولة)
توجد مجموعة نرمز لها ب ℂ وتحتوي على العدد الخيالي i الدي مربعه i²=-1
كل عدد z من ℂ يسمى عددا عقديا ويكتب على الشكل الوحيد z=a+ib حيث a;b∈IR .
1.1.2 امثلة :
z= 2+i3 ; z'=-3+i2; ...
1.1.3 مبرهنة 2 (مقبولة)
المجموعة ℂ تتضمن IR
وعمليات (الجمع والضرب) وخاصياتها تتمدد في المجموعة ℂ
لكن لا توجد علاقة ترتيب في ℂ يعني لا يمكن مقارنة عددين غير حقيقيين
1.1.4 الكتابة الجبرية لعدد عقدي
1- الكتابة a+ib حيث a;b∈IR, تسمى الشكل الجبري للعدد العقدي z=a+ib
2- العدد الحقيقي a يسمى الجزء الحقيقي للعدد العقدي z ونرمز له ب a=Re(z)
3- العدد الحقيقي b يسمى الجزء التخيلي للعدد العقدي z ونرمز له ب b=Im(z)
4- اذا كان a=0 فان العدد العقدي z يكتب على الشكل z=ib ويسمى z عددا تخيليا صرفا
امثلة
0=0i ; i8 ; i(-2) ; ..
1.2 تساوي عددين عقديين
1.2.1 العدد العقدي المنعدم
ليكن z=a+ib عددا عقديا بحيث a;b∈IR
a+ib =0 يكافئ a=0 و b=0
1.2.2 تساوي عددين عقديين
ليكن z=a+ib; z'=a'+ib'∈ℂ, a; b; a'; b'∈IR
z=z' ⇔ a=a' و b=b'
1.2.3 ميزة عدد حقيق وميزة عدد تخيلي صرفا
ليكن z=a+ib حيث a و b عددين حقيقيين
1- z∈ℝ ⇔ b=0
نرمز لمجموعة الاعداد العقدية الصرفة ب iIR
2- z∈iIR ⇔ a=0
1.2.4 ترميز
ليكن z=a+ib حيث a;b∈IR
يمكن كتابة z=a+ib على الشكل z=a+bi
امثلة : z=-3+2i ; z'=√7+5i; ..
1.3 مرافق عدد عقدي
1.3.1 تعريف
ليكن z=a+bi حيث a;b∈IR العدد العقدي a-bi يسمى مرافق العدد z ونرمز له ب z
1.3.2 امثلة :
7+3i=7-3i ; -2-i= -2+i
1.3.3 خاصيات
ليكن z و z' عددين عقديين z'≠0 ; k∈IR و n∈Z
z+z' = z + z' و
k.z = k.z
z.z' = z.z' ; z.z...z = (z)n
| ( | 1 | ) = | 1 |
| z | z | ( | z | ) = | z |
| z' | z' |
حدد مرافق كل من z و z'
z=(4-5i).(3+i)
| z'= | 4-5i |
| 3+i |
2- العمليات في المجموعة ℂ
2.1 خاصيات
a و b و a' و b' و k اعداد حقيقية
a+bi+a'+b'i=(a+a')+(b+b')i
k(a+bi)=ka+kbi
(a+bi).(a'+b'i)=aa'-bb'+(ab'+ba')i
(a+bi)²=a²-b²+2abi
(a-bi)²=a²-b²-2abi
(a+bi)(a-bi)=a²+b²
(bi)²=-b²
2.2 نتائج
ليكن a و b عددين حقيقيين وغير منعدمين
1) (a+bi).(a-bi)=a²+b²
| 1 | = | a-ib | (2 |
| a+ib | a²+b² |
كل عدد عقدي غير منعدم يقبل مقلوب
| a+ib | = | aa'+bb'+(ba'-ab')i | (3 |
| a'+ib' | a'²+b'² |
4) z=0 او z'=0 ⇔ ∀z; z'∈ ℂ: zz'=0
مثال 1
اكتب على الشكل الجبري كل من الاعداد التالية
z1=(2+3i)²
z2=2i(4+5i)
z3=(5-2i)²
تصحيح
z1=(2+3i)²= 4-9+12i=-5+12i
z2=2i(4+5i)=8i-10=-10+8i
z3=(5-2i)²=25-4-20i = 21-20i
مثال 2
1) احسب i³ ; i4 و i5
2) اكتب على الشكل الجبري للعدد z=(1+i)³
تصحيح
1) i³=-i ; i4=1 ; i5=i
2) z=(1+i)³= 1+3i+3i²+i³ = -2+2i
تمرين
اكتب على الشكل الجبري كل من الاعداد التالية
1) z=2+3i-0,5 +5i
2) z'=(1+4i)(2-5i)
3) z"=(2+5i)-1
3- المستوى العقدي
3.1 لحق نقطة ومتجهة
3.1.1 تعاريف
نعتبر (O;u→ ; v→) معلما متعامدا ممنظما
1) لكل عدد عقدي z=a+bi حيث a و b عددين حقيقيين , نربطه بالنقطة M(a;b)
نقول ان M نقطة صورة للعدد العقدي z والمتجهة OM→ هي متجهة صورة للعدد z
2) عكسيا لكل نقطة M(a;b) من المستوى نربطها بالعدد العقدي z=a+bi
نقول ان z لحق النقطة M وكذلك لحق المتجهة OM→
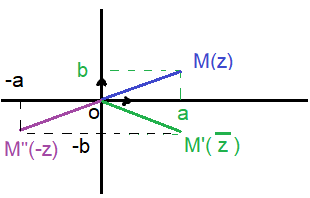
الترميز M(z) يعني ان النقطة M لحقها z
eوالترميز zM يعني ان z لحق النقطة M.
3.1.2 المستوى العقدي
1) مجموعة النقط M(z) حيث z∈ℂ تسمى المستوى العقدي
2) المحور (O,u→) يسمى محور الجزء الحقيقي والمحور (O;v→) محور الجزء التخيلي
3.2 لحق المتجهة AB→
لتكن A(z) و B(z') نقطتين من المستوى العقدي حيث z=x+yi و z'=x'+y'i
لدينا AB→=(x'-x)u→+(y'-y)v→ اذن لحق المتجهة AB→ هو العدد العقدي x'-x+(y'-y)i
ولدينا x'-x+(y'-y)i=(x'+y'i)-(x+yi)=z'-z
3.2.1 خاصية
لتكن A(z) و B(z') نقطتين من المستوى العقدي
لحق المتجهة AB→ هو ZAB→=z'-z
3.2.2 مثال
لتكن A(-4+3i) و B(-1+5i) نقطتين من المستوى العقدي
نحدد لحق المتجهة AB→
لدينا : aff(AB→)=-1-(-4)+i(5-3)
اذن aff(AB→)=3+2i.