3.3 لحق منتصف قطعة [AB]

I منتصف القطعة [AB]⇔ 2OI^→=OA^→+OB^→
اذن 2.aff(I)= z+z'

3.3.1 خاصية

لتكن A(z) و B(z') نقطتين من المستوى العقدي لحق المنتصف I للقطعة [AB] هو

aff(I)=	z+z'
	2

3.3.2 مثال

لتكن A(7+3i) و B(-1+5i) نقطتين من المستوى العقدي
حدد لحق منتصف القطعة [AB]

تصحيح

لدينا : aff(AB^→)=-8+2i
اذن aff(I)= -4+i

4- معيار عدد عقدي

4.1 تعريف

ليكن z∈ℂ و M(a;b) صورته في معلم
لدينا z=a+bi اذن OM=√(a²+b²) و z.z=a²+b²

4.1.1 تعريف

معيار عدد عقدي z هو عدد حقيقي موجب ونرمز له ب |z| ويساوي المسافة OM حيث M(z).
اي |z|=√(zz)=√(a²+b²)

4.1.2 مثال

|√2+i|=√(2+1)=√3 ; |4-3i|= 5

المسافة AB

AB=|Zb - Za|, A(Za) ; B(Zb)
امثلة:
A(1+2i) ; B(-3+5i) ; C(0,5+0,2i)
المسافة AB=|Zb-Za|=|-3+5i-(1+2i)|=|-4+3i|=√(16+9)=5
المسافة AC=|Zc-Za|=|0,5+0,2i-(1+2i) =|-0,5-1,8i|=√(0,25+3,24)=√(3,49)
المسافة BC=|Zc-Zb|=|0,5+0,2i-(-3+5i)| =|3,5+4,8i|=√(12,25+23,04)=√(35,29)

4.2 خاصيات

ليكن z;z'∈ℂ حيث z'≠0 و k∈IR و n∈Z
|-z|=|z|=|z| ; |z.z'| = |z|.|z'|

|	1	|=	1	; |	z	|=	|z|
	z'		|z'|		z'		|z'|

|zⁿ| = |z|ⁿ
|z + z'|≤|z|+|z'| ;(المتفاوتة المثلثية)
بصفة عامة

|	k=n ∏ k=1	zk|	=	k=n ∏ k=1	|zk|
|	k=n ∑ k=1	zk	|	≤	k=n ∑ k=1	|zk|

ملاحظة :

اذا كان z∈IR فان معيار العدد z هو القيمة المطلقة للعدد z

امثلة

|13|=13; |-27|=27;..

4.3 مجموعة الاعداد العقدية التي معيارها 1 (U,.)

𝕌={z∈ℂ/ |z|=1}
لدينا من جهة :
1∈𝕌 اذن 𝕌≠∅

ليكن z;z'∈𝕌
لدينا |z.z'|=|z|.|z'|=1.1=1 اذن zz'∈𝕌

z-1=	1
	z

اذن z^-1∈𝕌 ومنه فان (𝕌;.) زمرة فرعية ل (ℂ*;.) وبالتالي (𝕌;.) زمرة

خاصية

مجموعة الاعداد العقدية التي معيارها 1 (U,.) هي زمرة

4.4 الدائرة المثلثية

اذا كان z∈𝕌 و M(z) صورته
فان aff(OM^→)=z اذن |OM^→|=|z|=1
ومنه فان M نقطة من الدائرة المثلثية (C)
وعكسيا لتكن M∈(C) اذن تقبل لحق z∈ℂ بالاضافة الى ذلك |z|=OM=1 وبالتالي z∈𝕌

خاصية

مجموعة صور عناصر 𝕌 هي الدائرة المثلثية (C)

5- عمدة عدد عقدي غير منعدم

نعتبر المعلم المتعامد الممنظم المباشر (O;u^→;v^→) في المستوى العقدي

5.1 تعريف

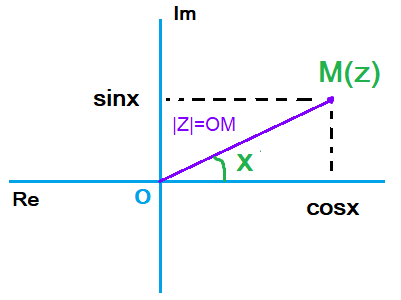
لتكن M(z), z∈ℂ, عمدة z ونرمز لها ب arg z, قياسا بالراديان للزاوية الموجهة (u^→; OM^→)
اذا كانت v^→ متجهة صورة للعدد العقدي z فان arg z=mes(u^→;v^→)+2kπ حيث k∈ℤ

5.2 خاصيات

5.2.1 ميزة عدد حقيقي

z∈IR ⇔ z=0 او arg z= 0+kπ; k∈ℤ

5.2.2 ميزة عدد تخيلي صرفا

z∈iIR ⇔ z=0 او arg z=(π/2)+kπ; k∈ℤ

5.2.3 ملاحظة :

0 ليس له عمدة ويعتبر عددا تخيلي صرفا

5.2.4 خاصيات

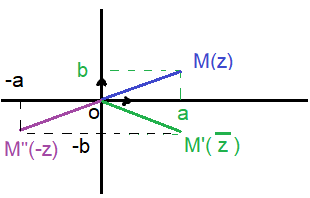
z∈ℂ*, arg(z)=- argz+2kπ; k∈ℤ
z∈ℂ*, arg(-z) =π+ argz + 2kπ; k∈ℤ

5.2.5 خاصيات

لتكن z;z'∈ℂ*
z=z' ⇔ | z |=| z' | و argz≡argz'[2π]
arg-z=π+argz +2kπ و argz=-argz+2kπ
argz.z'=argz+argz'+2kπ
argz.z...z = nargz + 2kπ ; k∈ℤ

arg	1	=-argz'+2kπ
	z'

arg	z	=argz-argz'+2kπ
	z'

امثلة

ليكن z و z' عددين عقديين اذا كان
argz=π/2 +2kπ و argz'=π/3 +2kπ حيث k∈ℤ
حدد arg(-z); arg(z); arg(z.z') و arg(z.z'^-1)

6- شكل مثلثي لعدد عقدي

6.1 خاصية وتعريف

6.1.1 خاصية

∀z∈ℂ*, ∃x∈ℝ : z=|z|(cosx + isinx)

6.1.2 تعريف

شكل مثلثي لعدد عقدي z هو الكتابة :
z=|z|(cosx+isinx) حيث x عمدة للعدد z.

6.1.3 مثال 1

حدد شكلا مثلثيا للعدد العقدي z=1+i

لدينا : | z |= √2
نحدد x بحيث cosx=1/√2 و sinx= 1/√2
لدينا cosπ/4 = sinπ/4 = (√2)/2 اذن
z= √2(cosπ/4 + isinπ/4) هي كتابة مثلثية للعدد العقدي z

6.2.3 مثال 2 ..

ليكن z=1-√(3)i
لدينا | z | = 2
نحدد x بحيث cosx = 1/2 و sinx = -√3/2
لدينا cos-π/3 = 1/2 و sin-π/3 = -√3/2 اذن كتابة مثلثية للعدد z هي
z= 2(cos-π/3 + isin-π/3)
ونكتب كذلك z = [2;-π/3]

6.2.3 خاصيات

ليكن z=[r;x] و z'=[r';x'] و n∈IN
-z = [r ; π + x] و z= [r ; -x]
z.z' =[rr'; x+x']

و zⁿ=[rⁿ;nx]

1	=[	1	;-x'] ;	z	=[	r	;x-x']
z'		r'		z'		r'

7 احداتيات قطبية

7.1 تقديم وتعريف

ليكن z=x+iy حيث x و y عددين حقيقيين
z لحق نقطة M لحق من المستوى العقدي المنسوب الى المعلم المتعامد الممنظم والمباشر (O;u^→;v^→)

x و y احداتيتان ديكارتيتان للنقطة M وللمتجهة OM^→ ونكتب M(x;y)
نضع OM=r و (u;OM)=θ[2π]
لدينا اذن z=rcosθ+risinθ =r(cosθ+isinθ)

7.1.1 تعريف

ليكن z∈ℂ* بحيث z=[r;θ]
r و θ هما احداتيتان قطبيتان للنقطة M ونكتب M(r;θ)

7.1.2 مثال

ليكن z= 1+i√3 لحق نقطة M
لدينا z=[2;π/3] اذن : (2;π/3) زوج احداتيتي قطبيتي للنقطة M ونكتب M(2;π/3)