Dérivation (1)
1- Dérivation d'une fonction
1.1 Dérivabilité et nombre dérivé (rappel)
1.1.1 Définition
Soit f une fonction définie sur un intérvalle I et a∈I. On dit que f est dérivable au point a s'il existe un nombre réel L tel que
lim h→0 |
f(a+h)-f(a) | = L |
| h |
L est appelé le Nombre dérivé de f en a et est noté f'(a).
Remarque Si on pose (a+h=x) on obtient
lim h→0 |
f(a+h)-f(a) | = | lim x→a |
f(x)-f(a) |
| h | x-a |
1.1.2 Interprétation géométrique
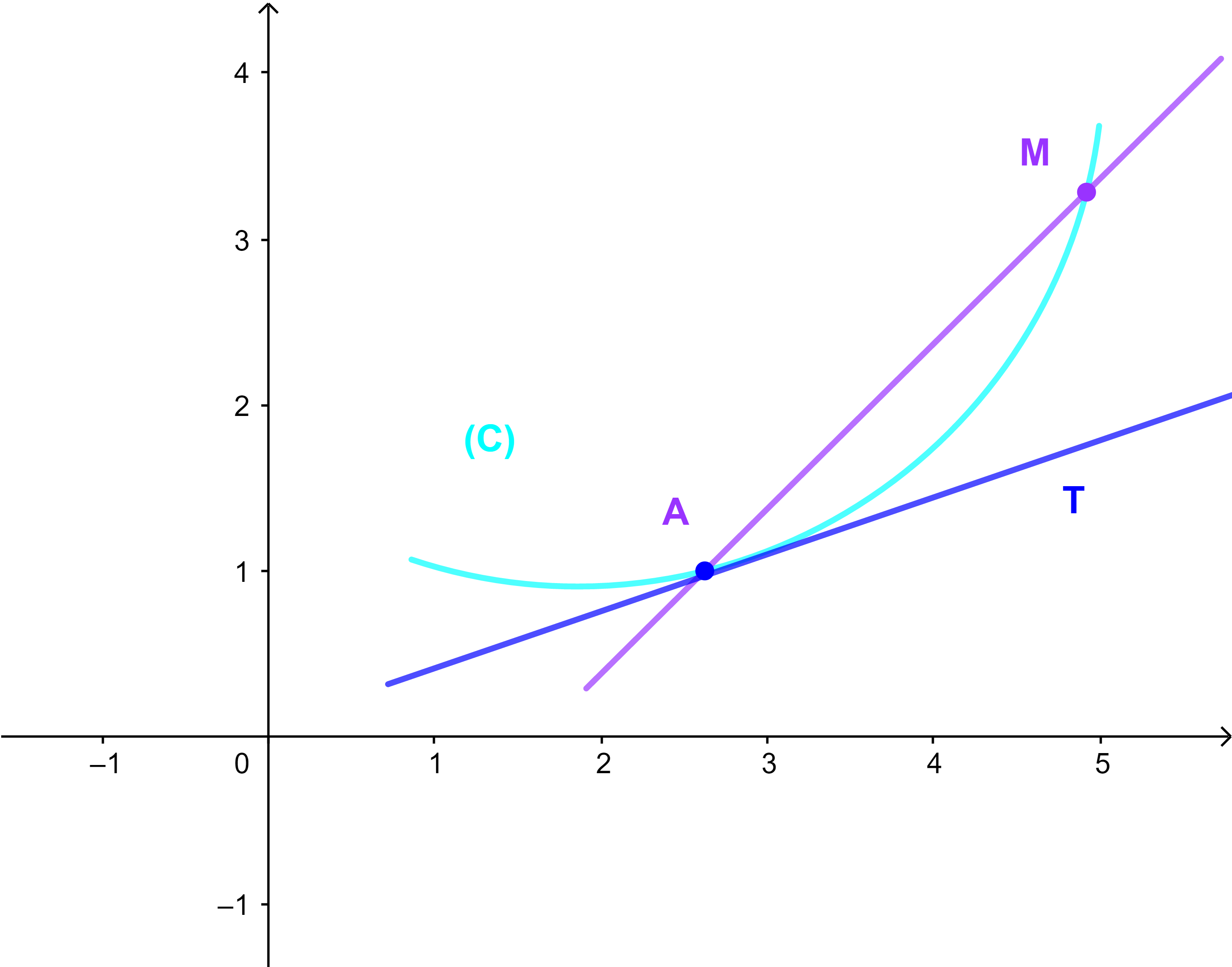
Soit f une fonction dérivable au point a et (C) sa courbe représentative dans un repère (O;i→;j→).
La courbe (C) admet une tangente
d'équation: y=f'(a)(x-a)+f(a) au point d'abscisse a.
1.1.3 Approximation affine
Soit f une fonction dérivable en a.
La fonction x→f'(a)(x-a)+f(a) est l'approximation affine de la fonction f au point a
(ou f(a+h)≃hf'(a)+f(a) avec h→0).
Exercice 1 tp
Soit f une fonction définie par f(x)=√(x).
1) Déterminer l'approximation affine de f(1+h)
au voisinage de 0 ?
2) Donner une valeur approximative de √(1,005).
Correction
On a f(a+h)≃hf'(a)+f(a) avec h→0
f(1)=1 il faut donc calculer le nombre
dérivé f'(1).
lim x→1 |
f(x)-f(1) | = | lim x→1 | 1 |
| x-1 | √(x)+1 |
donc f'(1)=0,5
et par conséquent f(1+h)≃(0,5)h+1.
Notons que √(1,005)=√(1+0,005)
0,005 s'approche de 0.
La fonction x→√(x)
est dérivable au point 1
donc f(1+0,005)≃0,005f'(1)+f(1)
ou encore √(1,005)≃0,005×(0,5)+1
ainsi √1,005 ≃1,0025.
Exercice 2 tp
Soit f une fonction définie par
| f(x) = | 1 |
| x |
1) Déterminer l'approximation affine de f(2+h)
au voisinage de 0 ?
2) Donner une valeur approximative de
| 1 |
| 2,005 |
Correction
On a f(a+h)≃hf'(a)+f(a) avec h→0 il faut donc calculer f(2) et le nombre dérivé f'(2).
lim 2 | f(x)-f(2) | = | lim 2 | -1 | = -0,25 |
| x-2 | 2x |
donc f'(2)=-0,25 et donc f(2+h)≃-0,25h+0,5.
2) 2,005 = 2+0,005 et f est dérivable au point 2
donc
f(2+0,005)≃0,005f'(2)+f(2)
ou encore f(2,005)≃0,005×(-0,25)+0,5
ainsi f(2,005) ≃0,49875.