الدوال الاسية (1)
1- الدالة الاسية النبيرية
1.1 تذكير وتعريف
1.1.1 مبرهنة القيمة الوسيطة :
لتكن f دالة متصلة ورتيبة قطعا على مجال I=[a;b] حيث a و b عددين حقيقيين و a < b
لكل عدد حقيقي k محصور بين f(a) و f(b) المعادلة f(x)=k تقبل حلا وحيدا على I.
1.1.2 دالة اللوغاريتم النبيري ln
دالة اللوغاريتم النبيري ln هي الدالة الاصلية للدالة
| x→ | 1 | x |
على IR*+ وتنعدم في 1 .
الدالة ln متصلة وتزايدية قطعا على IR*+
اذن الدالة ln تقبل دالة عكسية معرفة من IR نحو IR*+.
1.1.3 تعريف
الدالة العكسية للدالة ln تسمى الدالة الاسية ويرمز لها ب exp ومعرفة من IR نحو IR*+
بتعبير آخر
∀x∈IR: exp(x)=ln-1(x)
exp(x)=y, x∈IR ⇔ x=ln(y), y>0
1.1.3 مثال
exp(-2)=y, y>0 ⇔ lny=-2
exp(1)=y, y>0 ⇔lny=1, y=e
1.1.4 نتائج
1) ∀x∈IR, exp(x)>0
2) الدالة exp تزايدية قطعا على IR
3) ex=ey ⇔ x=y
4) ex < e x ⇔ x < y
1.1.5 الكتابة ex
لدينا ∀ r∈Q : lner=r
اذن er=exp(r)
ونعمم ذلك ∀x∈IR: exp(x)=ex
تمرين 1
حل في IR المعادلات التالية :
1) ex=5
2) ex=-3
3) (ex)²-5ex+4=0
تصحيح
1) المعادلة ex=5 معرفة في IR
ونعلم ان ex=5 ⇔ x=ln5
اذن S={ln5}
2) المعادلة ex=-3 مستحيلة لان لكل x∈IR لدينا ex>0 ولدينا 3- سالب اذن S=∅
3) المعادلة (ex)²-5ex+4=0 معرفة في IR
ونلاحظ انها معادلة من الدرجة الثانية وذلك بوضع ex=X
X²-5X+4=0
Δ=b²-4ac=(-5)²-4.4
=9 > 0
اذن هذه المعادلة تقبل حلين مختلفين
| X1= | -b-√Δ | ; | X2= | -b+√Δ |
| 2a | 2a |
| X1= | -(-5)-√9 | ; | X2= | -(-5)+√9 |
| 2.1 | 2.1 | |||
| X1= | 5-3 | ; | X2= | 5+3 |
| 2 | 2 | |||
| X1= | 2 | ; | X2= | 8 |
| 2 | 2 |
اذن
X1=1 و X2=4
المطلوب تحديد الحرف الصغير x
نعلم ان X=ex
الحالة الاولى
X1=1⇔ex1=1
⇔x1=ln1=0
الحالة الثانية :
X2=4⇔ex2=4
⇔x2=ln4
اذن S={0;ln4}
تمرين 2
حل في IR المتراجحات التالية
1) ex< 1
2) ex≥3
3) (ex)²-3ex-4 ≥0
تصحيح
1) المتراجحة ex< 1
معرفة على IR
ex< 1 ⇔ ln(ex) < ln1
⇔ x< 0 ⇔x∈]-∅;0[
S=]-∅;0[
2) المتراجحة ex≥3
معرفة على IR
ex≥3 ⇔ ln(ex) ≥ ln3
⇔ x≥ln3 ⇔x∈[ln3;+∞[
S=[ln3;∞[
3) المتراجحة (ex)²-3ex-4 ≥0 معرفة على IR
نضع X=ex>0 ونحصل على المتراجحة X²-3X-4≥0
اولا نحل المعادلة X²-3X-4=0 حيث ْX>0
Δ=(-3)²-4.(-4)=9+16=25>0
بنفس الطريقة كالتمرين السابق نجد
X1=-1 لا يمكن
و X2=4
ندرس الآن اشارة X²-3X-4 في ]0;+∞[
| X | 0 | 4 | +∞ | ||
| X²-3X-4 | || | - | 0 | + |
X²-3X-4≥0⇔X∈[4;+∞[
وبما ان X=ex فان
X≥4⇔ex≥4
⇔x≥ln4e
S=[ln4;+∞[
طريقة ثانية:
X²-3X-4=(X+1)(X-4)=(ex+1)(ex-4)
لدينا ex+1>0
اذن يكفي دراسة اشارة ex-4ومنه فان
ex-4≥0⇔ex≥4
⇔x≥ln4
S=[ln4;+∞[
تمرين 3
حل النظمة التالية :
| { | 2ex-3ey=1 |
| 5ex+2ex=12 |
تصحيح
نضع X=ex >0 ; Y=ey >0
النظمة تصبح اذن
| { | 2X-3Y=1 |
| 5X+2Y=12 |
يمكن استعمال اي طريق لحل النظمة ,سنستعمل مثلا طريقة التآلفية الخطية
2(2X-3Y-1)+3(5X+2Y-12)=0⇔19X=38⇔X=2
-5(2X-3Y-1)+2(5X+2Y-12)=0⇔19Y=19⇔Y=1
ومنه فان
X=2⇔ex2⇔x=ln2
Y=1⇔ey1⇔y=ln1=0
وبالتالي S={(ln2 ; 0)}
1.2 خاصيات جبرية
| x;y;r∈ℝ | |
| (ex)'= ex | |
| ex+y= ex . ey | |
| (ex)r=erx | |
| e-x= | 1 | ; ex-y = | ex |
| ex | ey |
تمرين
حل في IR المعادلة :
ex+2e-x-3=0
1.3 دراسة الدالة exp
1.3.1 مجموعة تعريف الدالة exp
exp معرفة من IR نحو IR*+ بتكوينها اذن
Dexp =IR
1.3.2 النهايات والفروع اللانهائية
lim+∞ex = +∞
lim-∞ ex = 0
اذن محور الافاصيل هو مقارب للمنحنى (C) بجوار -∞
| lim+∞ | ex | = +∞ |
| x |
اذن المنحنى (C) يقبل فرعا شلجميا في اتجاه محور الاراتيب
1.3.2 مشتقة الدالة exp
لدينا ∀x∈IR: ex> 0
الدالة exp قابلة للاشتقاق على IR و (ex)'= ex
برهان :
لدينا : ∀x∈IR, (ex)'=(ln-1)'(x)
| (ln-1)'(x)= | 1 | = | 1 |
| ln'(ln-1(x)) | ln(ln-1(x)) |
اذن (ex)' = ex
ومنه فان exp تزايدية قطعا على IR
| x | -∞ | +∞ | |
|---|---|---|---|
| f | 0 | ↗ | +∞ |
1.3.4 المنحنى
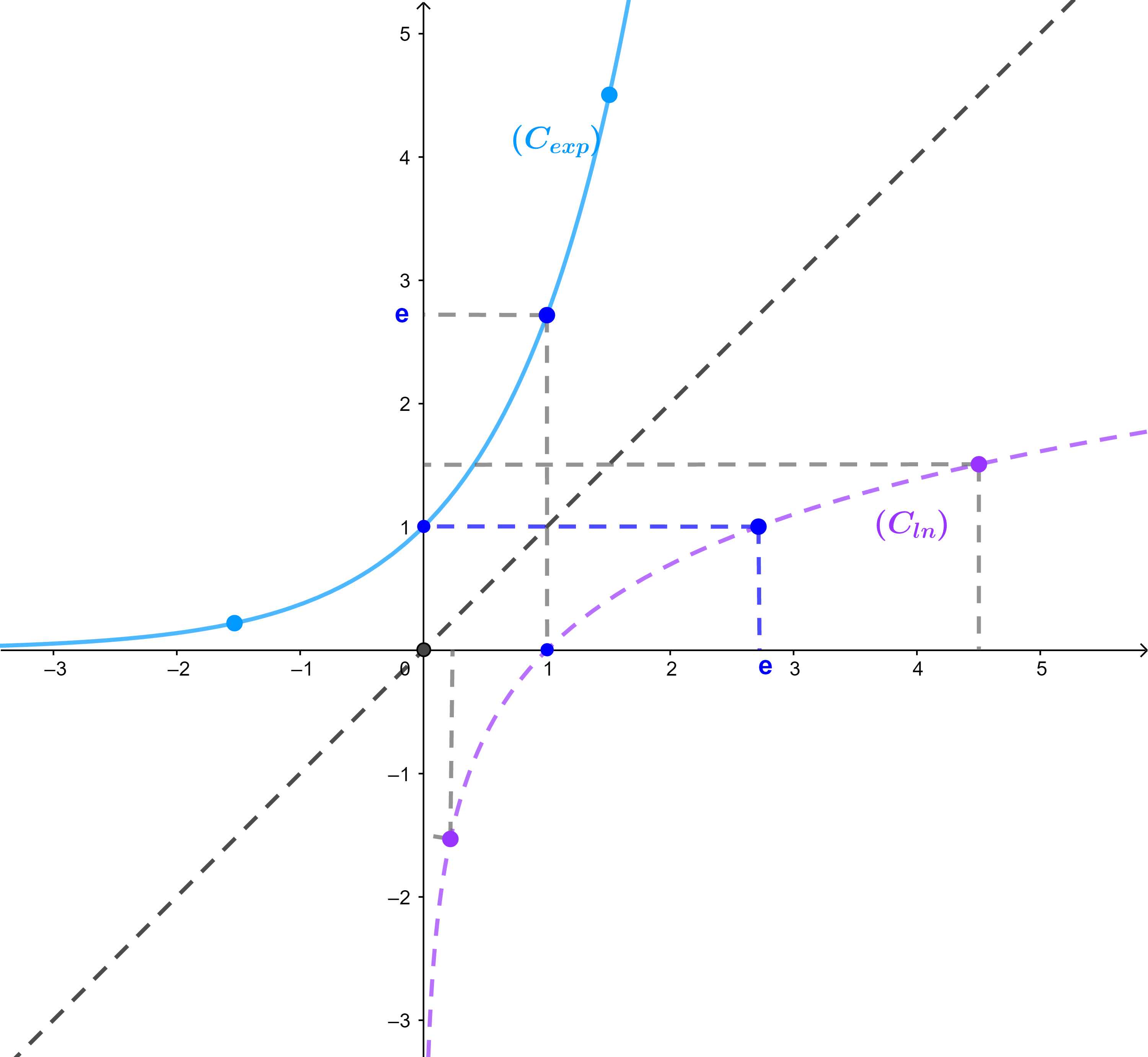
منحنى الدالة exp مماثل لمنحنى الدالة ln بالنسبة للمنصف الاول للمعلم اي المستقيم (D): y=x
1.3.5 نهايات اعتيادية
| lim+∞ ex = +∞ | ; | lim-∞ ex = 0 |
| limx->0 | ex-1 | = 1 |
| x | ||
| lim-∞xex= 0 | ; | lim-∞xnex=0 ; n∈Z |
| lim+∞ | ex | = +∞ |
| x | ||
| lim+∞ | ex | = +∞, n∈ℤ |
| xn |