Etude de fonctions numériques (3)
1.2 Point d’inflexion et concavité
1.2.1 Concavité d’une courbe
Définition Soit f une fonction dérivable sur un intervalle I et (C) sa courbe représentative dans un repère (O;i→;j→).
Si la courbe (C) est au-dessus de toutes ses tangentes
alors elle est convexe
(sa concavité est orientée vers les ordonnées positives).
Si la courbe (C) est au-dessous de toutes ses tangentes
alors elle est concave.
Exemples
1) Soit f une fonction définie par f(x)=2x²+1.
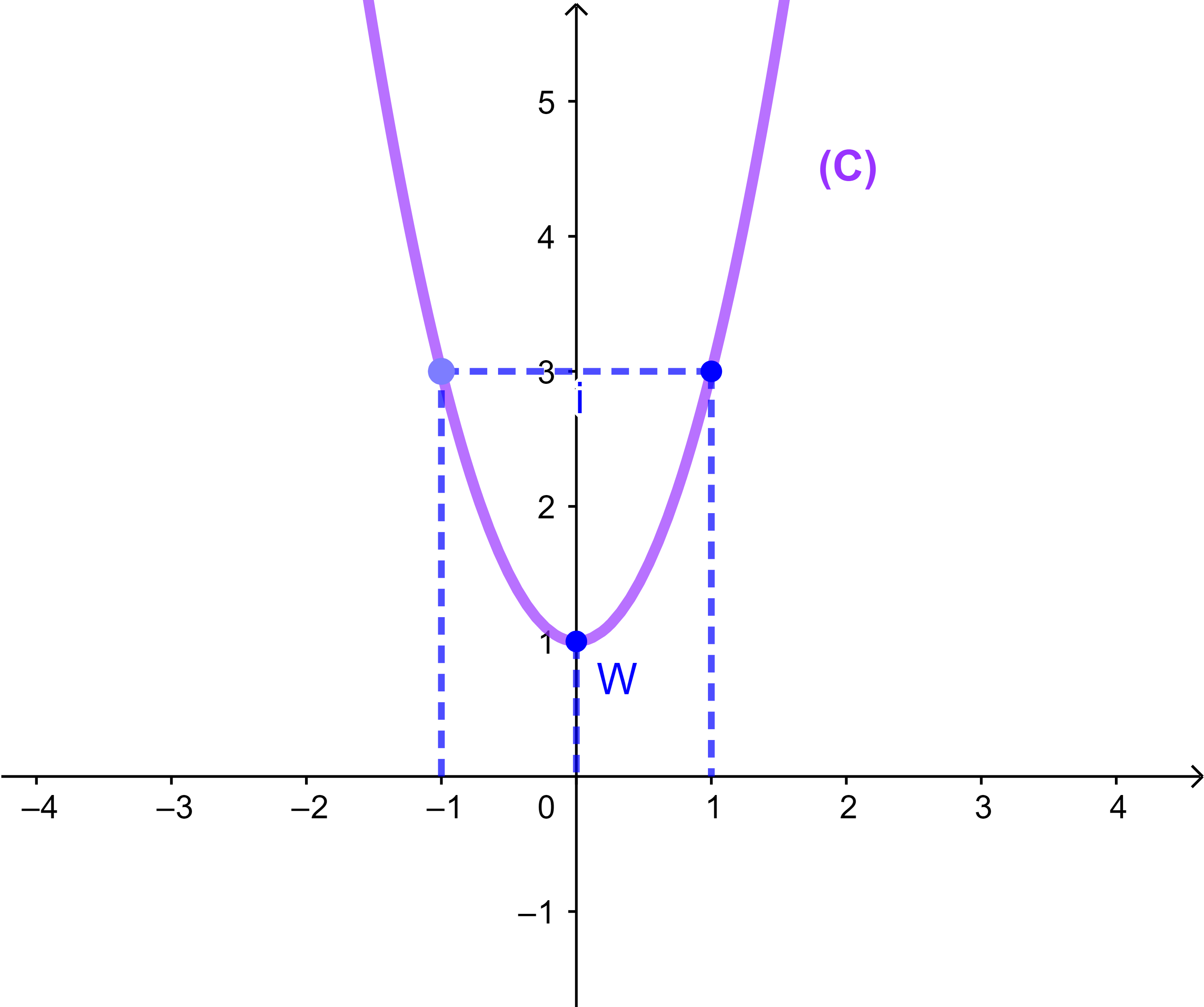
f est dérivble sur IR et sa courbe (C) est au-dessus de toutes ses tangentes dans IR
donc (C) est convexe.
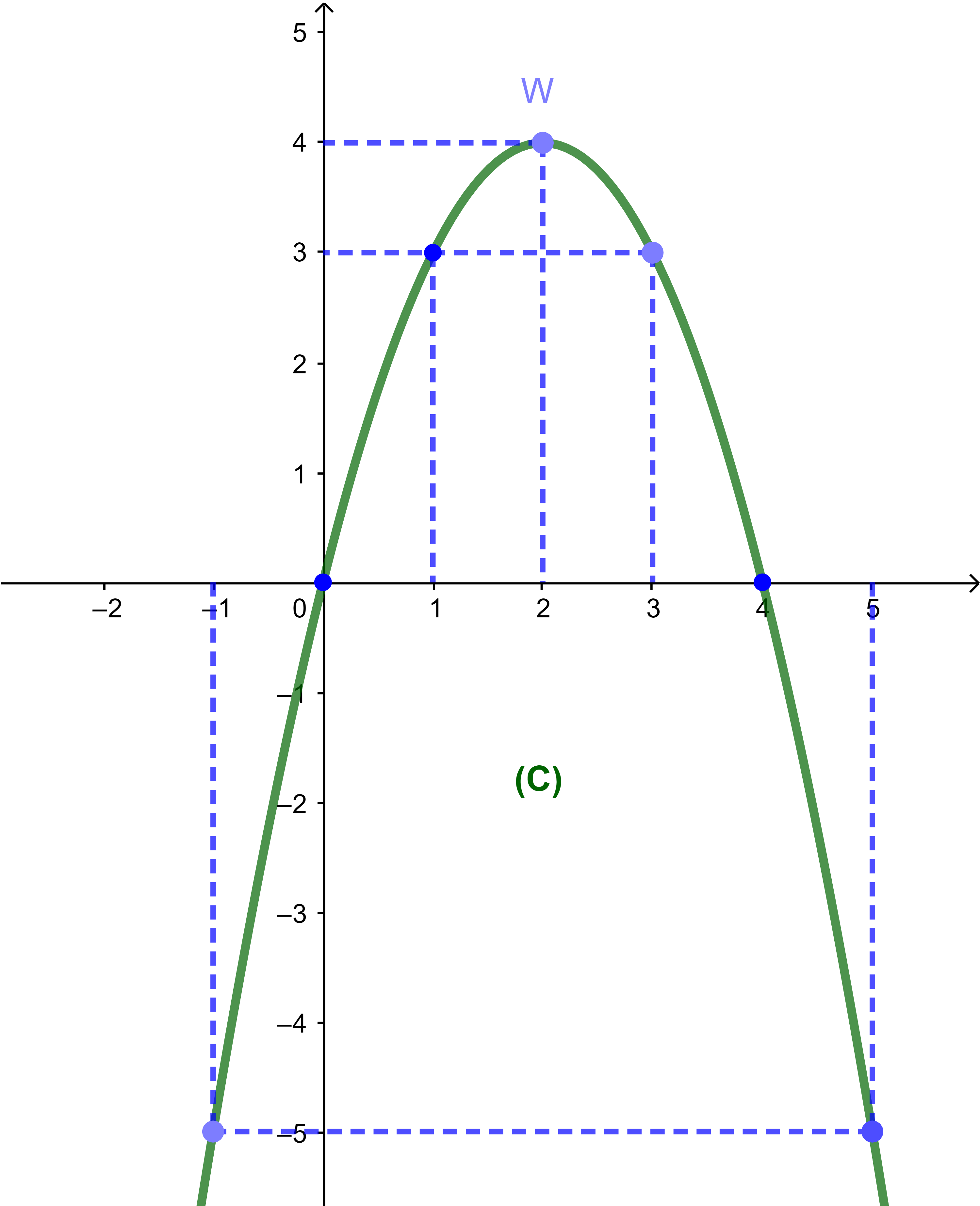
2) Soit f une fonction définie par f(x)=-x²+4x.
f est dérivable sur IR et sa courbe (C) est au-dessous de toutes ses tangentes dans IR
donc (C) est concave.
1.2.2 Point d’inflexion
Définition
Soit f une fonction dérivable sur intervalle I contenant a
et (C) sa courbe représentative dans un repère (O;i→;j→).
Le point A(a;f(a)) est un point
d'inflexion de (C) si la concavitée de (C) change
au point A.
Exemple
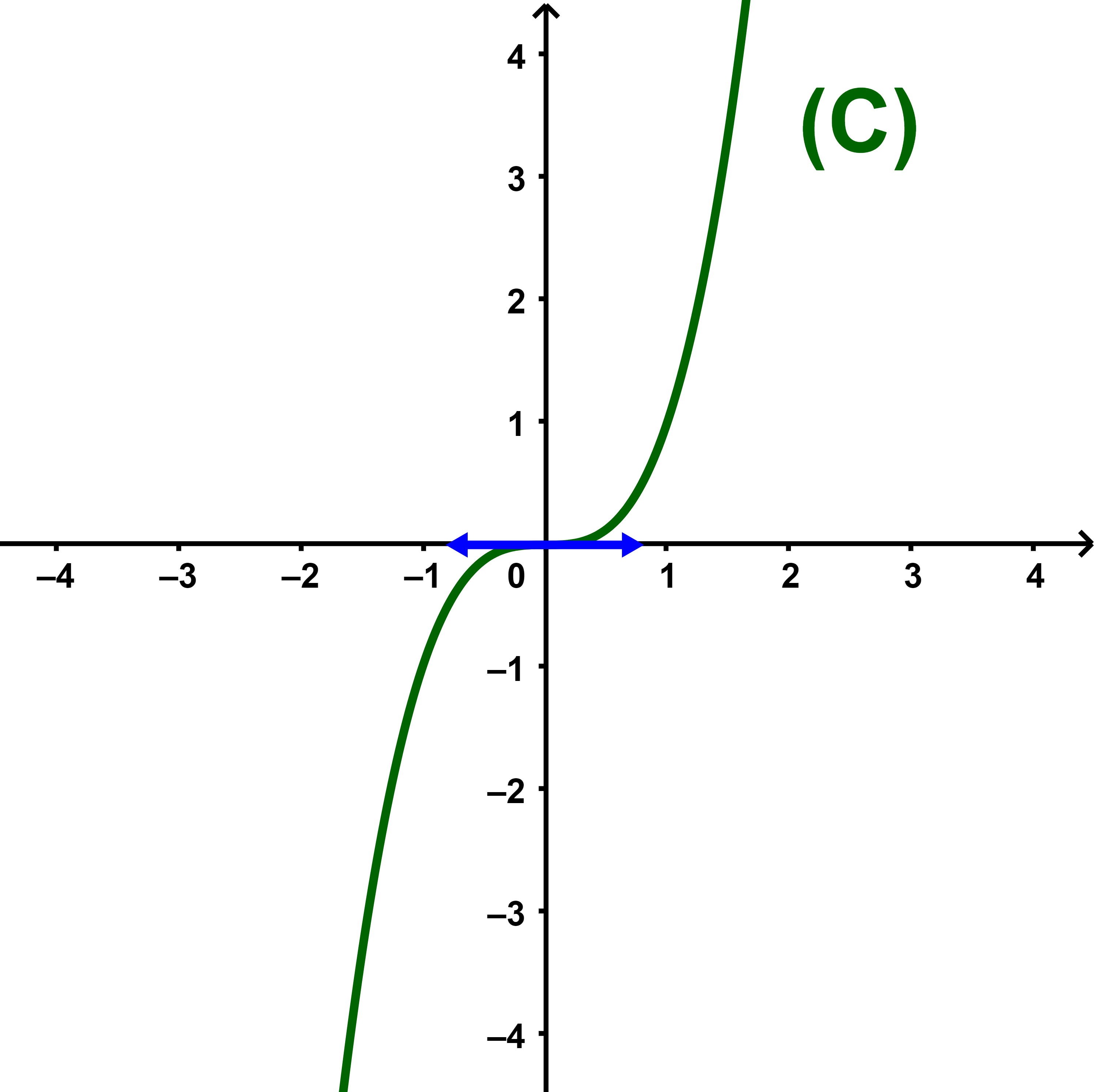
Soit f une fonction définie par f(x)= x³.
Le point O est un point d'inflexion de la courbe de f.
Propriétés
Soit f une fonction dérivable double sur un intervalle I et (C) sa courbe
représentative dans un repère (O;i→;j→).
1) Si (∀x∈I): f"(x)≥0 alors (C) est convexe.
2) Si (∀x∈I): f"(x)≤0 alors (C) est concave .
3) Si (∀x∈I): f"(a)=0 et f" change de signe au point a alors le point A(a;f(a)) est un point d'inflexion de la courbe (C).